Menu Close

Solve-for-real-numbers-4tan-x-sin-5x-cos-5-x-0-

Tinku Tara 0 Comments
Pin




Question Number 157964 by HongKing last updated on 30/Oct/21
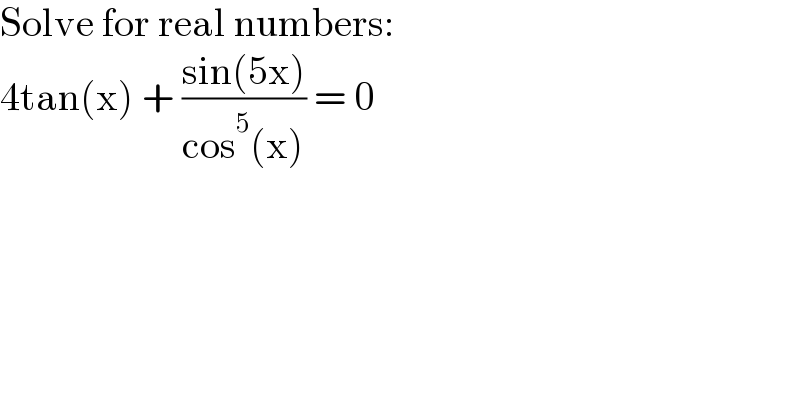
Solve for real numbers: 4tan(x) + ((sin(5x))/(cos^5 (x))) = 0
$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{real}\:\mathrm{numbers}: \\ $$$$\mathrm{4tan}\left(\mathrm{x}\right)\:+\:\frac{\mathrm{sin}\left(\mathrm{5x}\right)}{\mathrm{cos}^{\mathrm{5}} \left(\mathrm{x}\right)}\:=\:\mathrm{0} \\ $$$$ \\ $$
Commented by tounghoungko last updated on 30/Oct/21
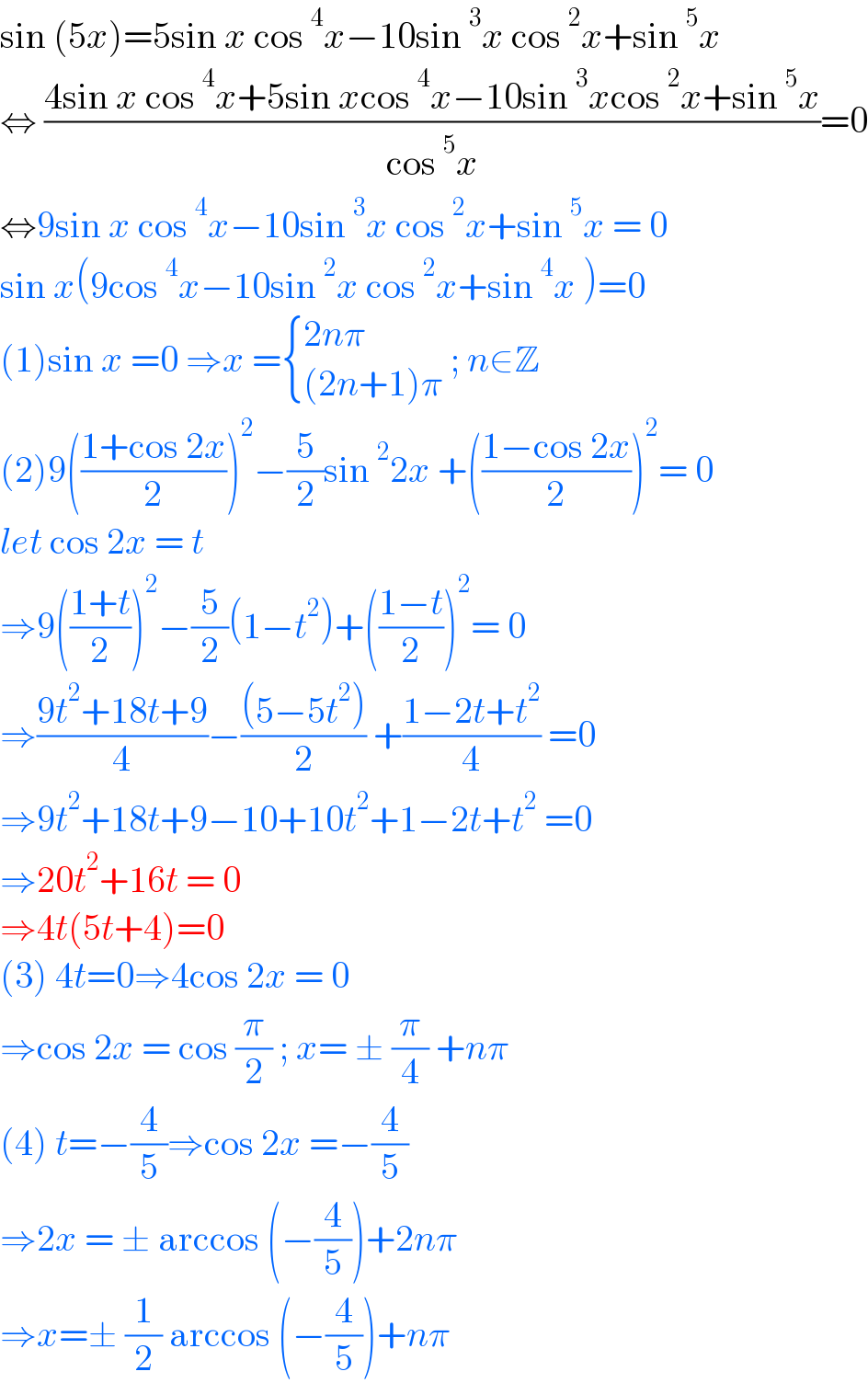
sin (5x)=5sin x cos^4 x−10sin^3 x cos^2 x+sin^5 x ⇔ ((4sin x cos^4 x+5sin xcos^4 x−10sin^3 xcos^2 x+sin^5 x)/(cos^5 x))=0 ⇔9sin x cos^4 x−10sin^3 x cos^2 x+sin^5 x = 0 sin x(9cos^4 x−10sin^2 x cos^2 x+sin^4 x )=0 (1)sin x =0 ⇒x = { ((2nπ)),(((2n+1)π)) :} ; n∈Z (2)9(((1+cos 2x)/2))^2 −(5/2)sin^2 2x +(((1−cos 2x)/2))^2 = 0 let cos 2x = t ⇒9(((1+t)/2))^2 −(5/2)(1−t^2 )+(((1−t)/2))^2 = 0 ⇒((9t^2 +18t+9)/4)−(((5−5t^2 ))/2) +((1−2t+t^2 )/4) =0 ⇒9t^2 +18t+9−10+10t^2 +1−2t+t^2 =0 ⇒20t^2 +16t = 0 ⇒4t(5t+4)=0 (3) 4t=0⇒4cos 2x = 0 ⇒cos 2x = cos (π/2) ; x= ± (π/4) +nπ (4) t=−(4/5)⇒cos 2x =−(4/5) ⇒2x = ± arccos (−(4/5))+2nπ ⇒x=± (1/2) arccos (−(4/5))+nπ
$$\mathrm{sin}\:\left(\mathrm{5}{x}\right)=\mathrm{5sin}\:{x}\:\mathrm{cos}\:^{\mathrm{4}} {x}−\mathrm{10sin}\:^{\mathrm{3}} {x}\:\mathrm{cos}\:^{\mathrm{2}} {x}+\mathrm{sin}\:^{\mathrm{5}} {x} \\ $$$$\Leftrightarrow\:\frac{\mathrm{4sin}\:{x}\:\mathrm{cos}\:^{\mathrm{4}} {x}+\mathrm{5sin}\:{x}\mathrm{cos}\:^{\mathrm{4}} {x}−\mathrm{10sin}\:^{\mathrm{3}} {x}\mathrm{cos}\:^{\mathrm{2}} {x}+\mathrm{sin}\:^{\mathrm{5}} {x}}{\mathrm{cos}\:^{\mathrm{5}} {x}}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{9sin}\:{x}\:\mathrm{cos}\:^{\mathrm{4}} {x}−\mathrm{10sin}\:^{\mathrm{3}} {x}\:\mathrm{cos}\:^{\mathrm{2}} {x}+\mathrm{sin}\:^{\mathrm{5}} {x}\:=\:\mathrm{0} \\ $$$$\mathrm{sin}\:{x}\left(\mathrm{9cos}\:^{\mathrm{4}} {x}−\mathrm{10sin}\:^{\mathrm{2}} {x}\:\mathrm{cos}\:^{\mathrm{2}} {x}+\mathrm{sin}\:^{\mathrm{4}} {x}\:\right)=\mathrm{0} \\ $$$$\left(\mathrm{1}\right)\mathrm{sin}\:{x}\:=\mathrm{0}\:\Rightarrow{x}\:=\begin{cases}{\mathrm{2}{n}\pi}\\{\left(\mathrm{2}{n}+\mathrm{1}\right)\pi}\end{cases}\:;\:{n}\in\mathbb{Z} \\ $$$$\left(\mathrm{2}\right)\mathrm{9}\left(\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{5}}{\mathrm{2}}\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}{x}\:+\left(\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{2}}\right)^{\mathrm{2}} =\:\mathrm{0} \\ $$$${let}\:\mathrm{cos}\:\mathrm{2}{x}\:=\:{t} \\ $$$$\Rightarrow\mathrm{9}\left(\frac{\mathrm{1}+{t}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{5}}{\mathrm{2}}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)+\left(\frac{\mathrm{1}−{t}}{\mathrm{2}}\right)^{\mathrm{2}} =\:\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{9}{t}^{\mathrm{2}} +\mathrm{18}{t}+\mathrm{9}}{\mathrm{4}}−\frac{\left(\mathrm{5}−\mathrm{5}{t}^{\mathrm{2}} \right)}{\mathrm{2}}\:+\frac{\mathrm{1}−\mathrm{2}{t}+{t}^{\mathrm{2}} }{\mathrm{4}}\:=\mathrm{0} \\ $$$$\Rightarrow\mathrm{9}{t}^{\mathrm{2}} +\mathrm{18}{t}+\mathrm{9}−\mathrm{10}+\mathrm{10}{t}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{t}+{t}^{\mathrm{2}} \:=\mathrm{0} \\ $$$$\Rightarrow\mathrm{20}{t}^{\mathrm{2}} +\mathrm{16}{t}\:=\:\mathrm{0} \\ $$$$\Rightarrow\mathrm{4}{t}\left(\mathrm{5}{t}+\mathrm{4}\right)=\mathrm{0} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{4}{t}=\mathrm{0}\Rightarrow\mathrm{4cos}\:\mathrm{2}{x}\:=\:\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}\:\mathrm{2}{x}\:=\:\mathrm{cos}\:\frac{\pi}{\mathrm{2}}\:;\:{x}=\:\pm\:\frac{\pi}{\mathrm{4}}\:+{n}\pi \\ $$$$\left(\mathrm{4}\right)\:{t}=−\frac{\mathrm{4}}{\mathrm{5}}\Rightarrow\mathrm{cos}\:\mathrm{2}{x}\:=−\frac{\mathrm{4}}{\mathrm{5}}\: \\ $$$$\Rightarrow\mathrm{2}{x}\:=\:\pm\:\mathrm{arccos}\:\left(−\frac{\mathrm{4}}{\mathrm{5}}\right)+\mathrm{2}{n}\pi \\ $$$$\Rightarrow{x}=\pm\:\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{arccos}\:\left(−\frac{\mathrm{4}}{\mathrm{5}}\right)+{n}\pi\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *