Question Number 162102 by HongKing last updated on 26/Dec/21
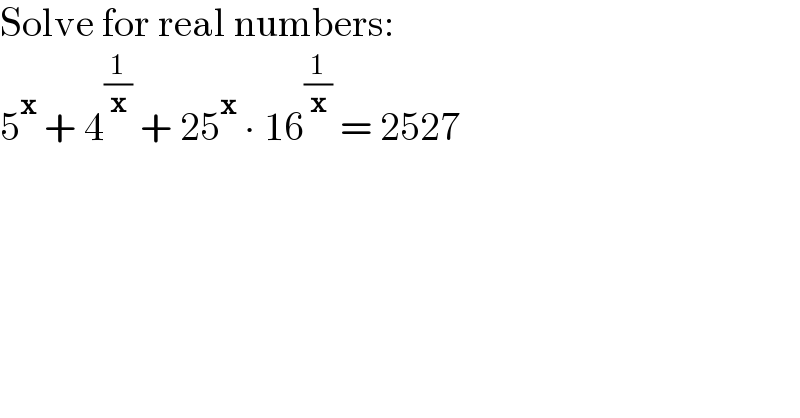
$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{real}\:\mathrm{numbers}: \\ $$$$\mathrm{5}^{\boldsymbol{\mathrm{x}}} \:+\:\mathrm{4}^{\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}} \:+\:\mathrm{25}^{\boldsymbol{\mathrm{x}}} \:\centerdot\:\mathrm{16}^{\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}} \:=\:\mathrm{2527} \\ $$
Commented by mr W last updated on 26/Dec/21
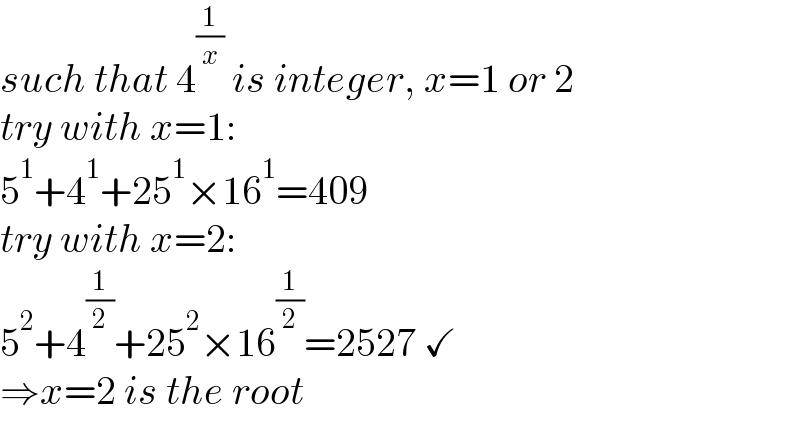
$${such}\:{that}\:\mathrm{4}^{\frac{\mathrm{1}}{{x}}} \:{is}\:{integer},\:{x}=\mathrm{1}\:{or}\:\mathrm{2} \\ $$$${try}\:{with}\:{x}=\mathrm{1}: \\ $$$$\mathrm{5}^{\mathrm{1}} +\mathrm{4}^{\mathrm{1}} +\mathrm{25}^{\mathrm{1}} ×\mathrm{16}^{\mathrm{1}} =\mathrm{409} \\ $$$${try}\:{with}\:{x}=\mathrm{2}: \\ $$$$\mathrm{5}^{\mathrm{2}} +\mathrm{4}^{\frac{\mathrm{1}}{\mathrm{2}}} +\mathrm{25}^{\mathrm{2}} ×\mathrm{16}^{\frac{\mathrm{1}}{\mathrm{2}}} =\mathrm{2527}\:\checkmark \\ $$$$\Rightarrow{x}=\mathrm{2}\:{is}\:{the}\:{root} \\ $$
Commented by HongKing last updated on 28/Dec/21
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{Sir} \\ $$
