Question Number 157044 by MathSh last updated on 18/Oct/21
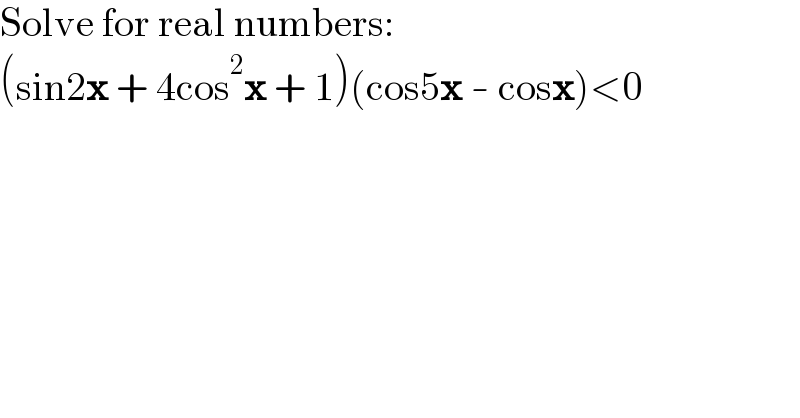
$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{real}\:\mathrm{numbers}: \\ $$$$\left(\mathrm{sin2}\boldsymbol{\mathrm{x}}\:+\:\mathrm{4cos}^{\mathrm{2}} \boldsymbol{\mathrm{x}}\:+\:\mathrm{1}\right)\left(\mathrm{cos5}\boldsymbol{\mathrm{x}}\:-\:\mathrm{cos}\boldsymbol{\mathrm{x}}\right)<\mathrm{0} \\ $$
Answered by mindispower last updated on 19/Oct/21
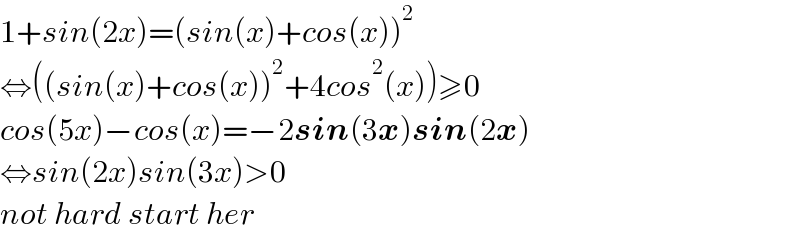
$$\mathrm{1}+{sin}\left(\mathrm{2}{x}\right)=\left({sin}\left({x}\right)+{cos}\left({x}\right)\right)^{\mathrm{2}} \\ $$$$\Leftrightarrow\left(\left({sin}\left({x}\right)+{cos}\left({x}\right)\right)^{\mathrm{2}} +\mathrm{4}{cos}^{\mathrm{2}} \left({x}\right)\right)\geqslant\mathrm{0} \\ $$$${cos}\left(\mathrm{5}{x}\right)−{cos}\left({x}\right)=−\mathrm{2}\boldsymbol{{sin}}\left(\mathrm{3}\boldsymbol{{x}}\right)\boldsymbol{{sin}}\left(\mathrm{2}\boldsymbol{{x}}\right) \\ $$$$\Leftrightarrow{sin}\left(\mathrm{2}{x}\right){sin}\left(\mathrm{3}{x}\right)>\mathrm{0} \\ $$$${not}\:{hard}\:{start}\:{her}\: \\ $$
Commented by MathSh last updated on 19/Oct/21
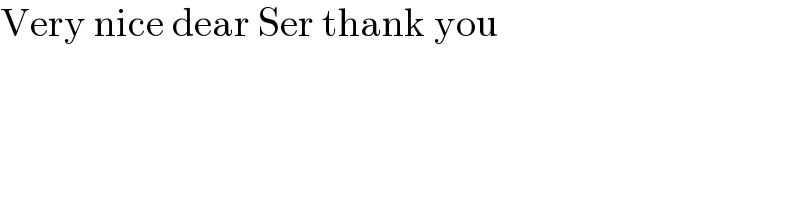
$$\mathrm{Very}\:\mathrm{nice}\:\mathrm{dear}\:\mathrm{Ser}\:\mathrm{thank}\:\mathrm{you} \\ $$
Commented by mindispower last updated on 19/Oct/21

$${withe}\:{pleasur} \\ $$
