Question Number 149478 by mathdanisur last updated on 05/Aug/21
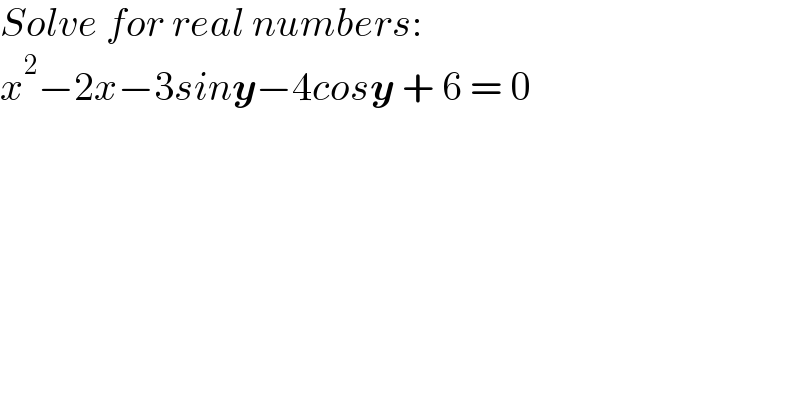
$${Solve}\:{for}\:{real}\:{numbers}: \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{3}{sin}\boldsymbol{{y}}−\mathrm{4}{cos}\boldsymbol{{y}}\:+\:\mathrm{6}\:=\:\mathrm{0} \\ $$
Commented by iloveisrael last updated on 06/Aug/21
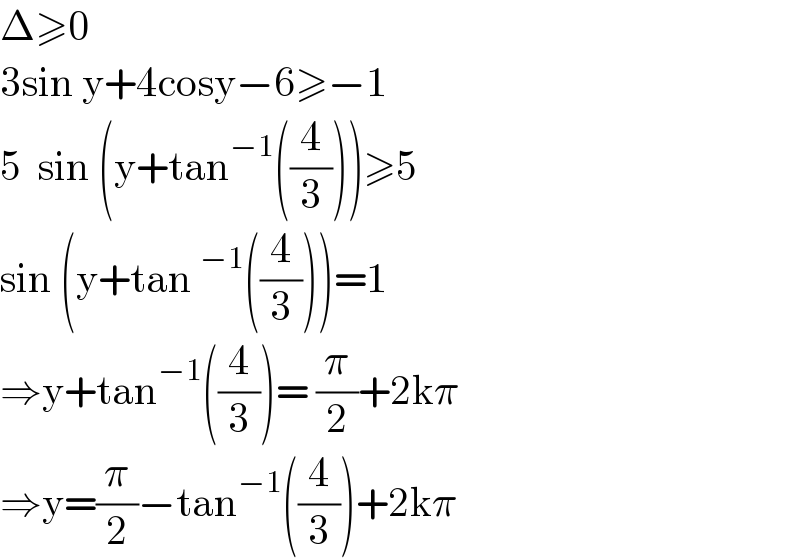
$$\Delta\geqslant\mathrm{0} \\ $$$$\mathrm{3sin}\:\mathrm{y}+\mathrm{4cosy}−\mathrm{6}\geqslant−\mathrm{1} \\ $$$$\mathrm{5}\:\:\mathrm{sin}\:\left(\mathrm{y}+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{4}}{\mathrm{3}}\right)\right)\geqslant\mathrm{5} \\ $$$$\mathrm{sin}\:\left(\mathrm{y}+\mathrm{tan}\:^{−\mathrm{1}} \left(\frac{\mathrm{4}}{\mathrm{3}}\right)\right)=\mathrm{1} \\ $$$$\Rightarrow\mathrm{y}+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{4}}{\mathrm{3}}\right)=\:\frac{\pi}{\mathrm{2}}+\mathrm{2k}\pi \\ $$$$\Rightarrow\mathrm{y}=\frac{\pi}{\mathrm{2}}−\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{4}}{\mathrm{3}}\right)+\mathrm{2k}\pi \\ $$
Commented by mathdanisur last updated on 06/Aug/21

$$\mathrm{Thankyou}\:\boldsymbol{\mathrm{Ser}} \\ $$
Answered by mr W last updated on 05/Aug/21
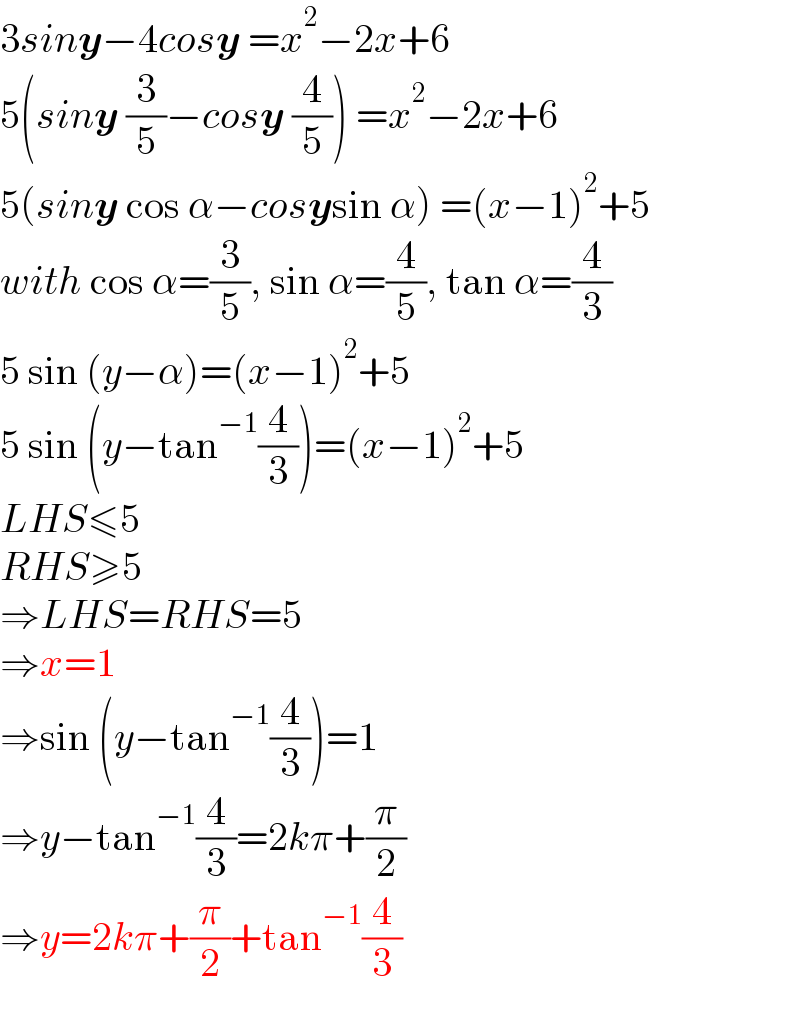
$$\mathrm{3}{sin}\boldsymbol{{y}}−\mathrm{4}{cos}\boldsymbol{{y}}\:={x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{6} \\ $$$$\mathrm{5}\left({sin}\boldsymbol{{y}}\:\frac{\mathrm{3}}{\mathrm{5}}−{cos}\boldsymbol{{y}}\:\frac{\mathrm{4}}{\mathrm{5}}\right)\:={x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{6} \\ $$$$\mathrm{5}\left({sin}\boldsymbol{{y}}\:\mathrm{cos}\:\alpha−{cos}\boldsymbol{{y}}\mathrm{sin}\:\alpha\right)\:=\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{5} \\ $$$${with}\:\mathrm{cos}\:\alpha=\frac{\mathrm{3}}{\mathrm{5}},\:\mathrm{sin}\:\alpha=\frac{\mathrm{4}}{\mathrm{5}},\:\mathrm{tan}\:\alpha=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\mathrm{5}\:\mathrm{sin}\:\left({y}−\alpha\right)=\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{5} \\ $$$$\mathrm{5}\:\mathrm{sin}\:\left({y}−\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{3}}\right)=\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{5} \\ $$$${LHS}\leqslant\mathrm{5} \\ $$$${RHS}\geqslant\mathrm{5} \\ $$$$\Rightarrow{LHS}={RHS}=\mathrm{5} \\ $$$$\Rightarrow{x}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{sin}\:\left({y}−\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{3}}\right)=\mathrm{1} \\ $$$$\Rightarrow{y}−\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{3}}=\mathrm{2}{k}\pi+\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow{y}=\mathrm{2}{k}\pi+\frac{\pi}{\mathrm{2}}+\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{3}} \\ $$
Commented by mathdanisur last updated on 05/Aug/21

$$\mathrm{Thank}\:\mathrm{you}\:\boldsymbol{\mathrm{Ser}},\:\mathrm{cool} \\ $$
Commented by peter frank last updated on 05/Aug/21
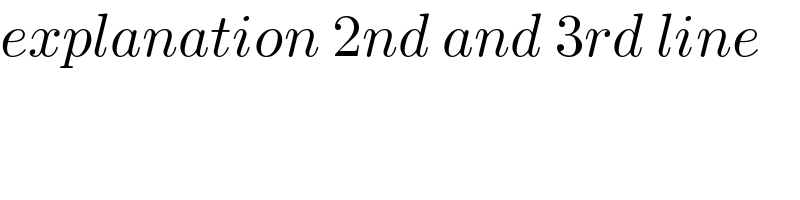
$${explanation}\:\mathrm{2}{nd}\:{and}\:\mathrm{3}{rd}\:{line} \\ $$
Commented by mr W last updated on 05/Aug/21
$${i}\:{added}\:{some}\:{lines}\:{more}. \\ $$
Commented by peter frank last updated on 05/Aug/21

$${thank}\:{you} \\ $$
Commented by Tawa11 last updated on 05/Aug/21

$$\mathrm{great} \\ $$
Answered by MJS_new last updated on 05/Aug/21
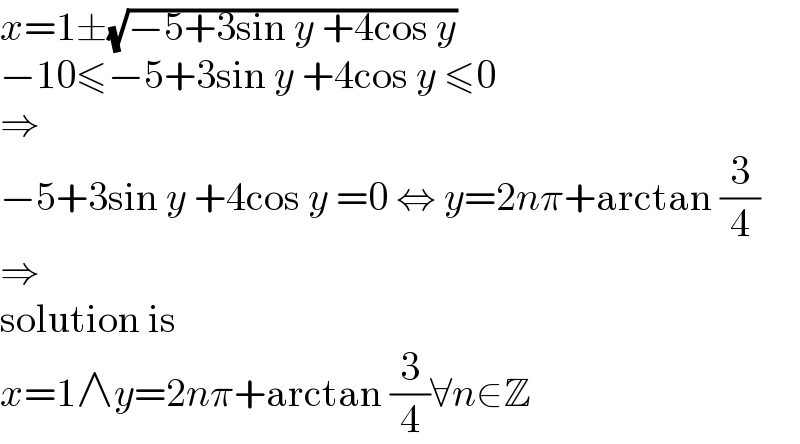
$${x}=\mathrm{1}\pm\sqrt{−\mathrm{5}+\mathrm{3sin}\:{y}\:+\mathrm{4cos}\:{y}} \\ $$$$−\mathrm{10}\leqslant−\mathrm{5}+\mathrm{3sin}\:{y}\:+\mathrm{4cos}\:{y}\:\leqslant\mathrm{0} \\ $$$$\Rightarrow \\ $$$$−\mathrm{5}+\mathrm{3sin}\:{y}\:+\mathrm{4cos}\:{y}\:=\mathrm{0}\:\Leftrightarrow\:{y}=\mathrm{2}{n}\pi+\mathrm{arctan}\:\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow \\ $$$$\mathrm{solution}\:\mathrm{is} \\ $$$${x}=\mathrm{1}\wedge{y}=\mathrm{2}{n}\pi+\mathrm{arctan}\:\frac{\mathrm{3}}{\mathrm{4}}\forall{n}\in\mathbb{Z} \\ $$
Commented by mathdanisur last updated on 05/Aug/21

$$\mathrm{Thank}\:\mathrm{you}\:\boldsymbol{\mathrm{Ser}},\:\mathrm{cool} \\ $$
