Question Number 155106 by mathdanisur last updated on 25/Sep/21
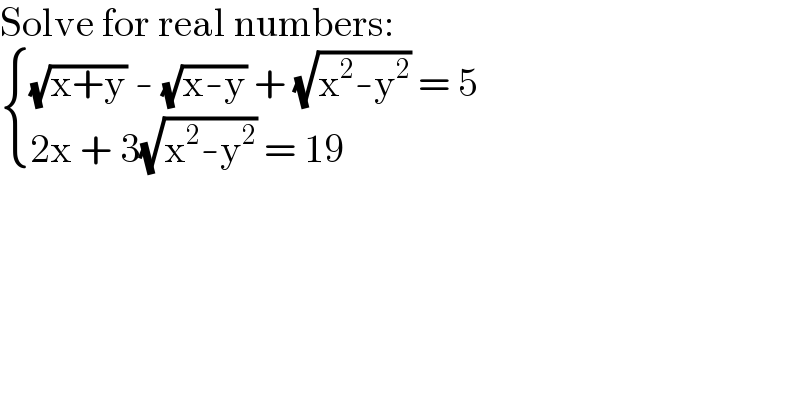
$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{real}\:\mathrm{numbers}: \\ $$$$\begin{cases}{\sqrt{\mathrm{x}+\mathrm{y}}\:-\:\sqrt{\mathrm{x}-\mathrm{y}}\:+\:\sqrt{\mathrm{x}^{\mathrm{2}} -\mathrm{y}^{\mathrm{2}} }\:=\:\mathrm{5}}\\{\mathrm{2x}\:+\:\mathrm{3}\sqrt{\mathrm{x}^{\mathrm{2}} -\mathrm{y}^{\mathrm{2}} }\:=\:\mathrm{19}}\end{cases} \\ $$
Commented by benhamimed last updated on 25/Sep/21
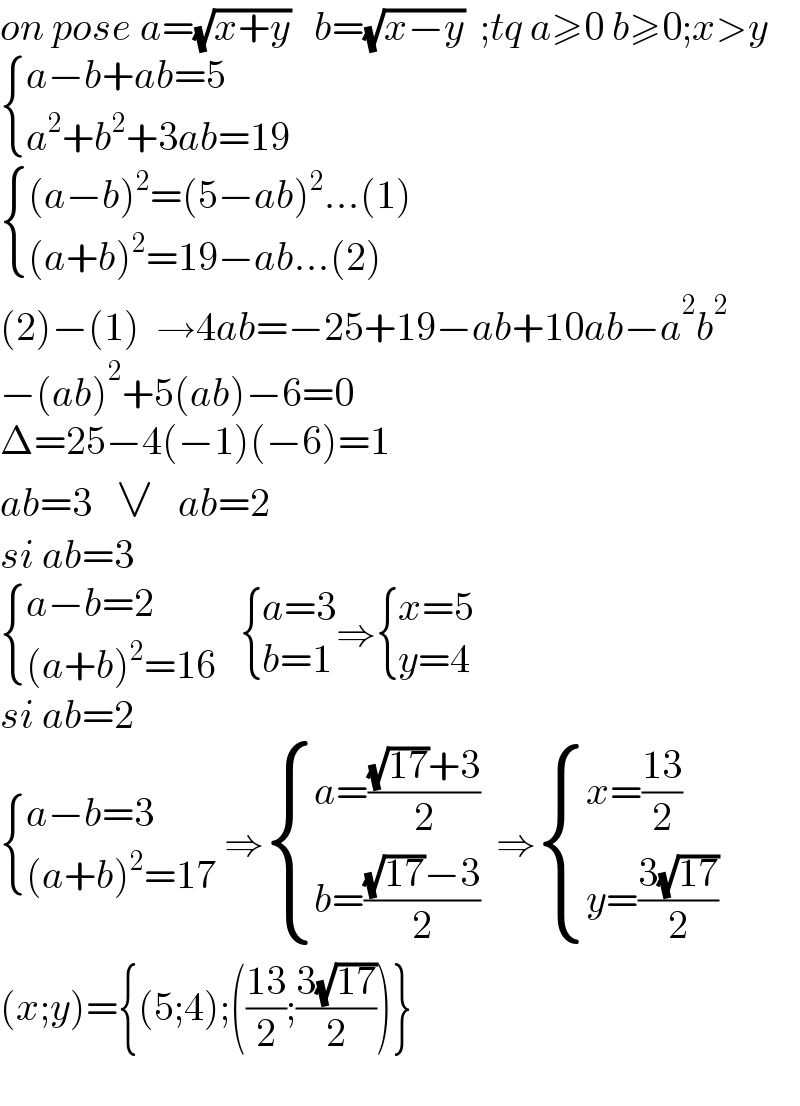
$${on}\:{pose}\:{a}=\sqrt{{x}+{y}}\:\:\:{b}=\sqrt{{x}−{y}}\:\:;{tq}\:{a}\geqslant\mathrm{0}\:{b}\geqslant\mathrm{0};{x}>{y} \\ $$$$\begin{cases}{{a}−{b}+{ab}=\mathrm{5}}\\{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{3}{ab}=\mathrm{19}}\end{cases} \\ $$$$\begin{cases}{\left({a}−{b}\right)^{\mathrm{2}} =\left(\mathrm{5}−{ab}\right)^{\mathrm{2}} …\left(\mathrm{1}\right)}\\{\left({a}+{b}\right)^{\mathrm{2}} =\mathrm{19}−{ab}…\left(\mathrm{2}\right)}\end{cases} \\ $$$$\left(\mathrm{2}\right)−\left(\mathrm{1}\right)\:\:\rightarrow\mathrm{4}{ab}=−\mathrm{25}+\mathrm{19}−{ab}+\mathrm{10}{ab}−{a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$$−\left({ab}\right)^{\mathrm{2}} +\mathrm{5}\left({ab}\right)−\mathrm{6}=\mathrm{0} \\ $$$$\Delta=\mathrm{25}−\mathrm{4}\left(−\mathrm{1}\right)\left(−\mathrm{6}\right)=\mathrm{1} \\ $$$${ab}=\mathrm{3}\:\:\:\vee\:\:\:{ab}=\mathrm{2} \\ $$$${si}\:{ab}=\mathrm{3} \\ $$$$\begin{cases}{{a}−{b}=\mathrm{2}}\\{\left({a}+{b}\right)^{\mathrm{2}} =\mathrm{16}}\end{cases}\:\:\:\begin{cases}{{a}=\mathrm{3}}\\{{b}=\mathrm{1}}\end{cases}\Rightarrow\begin{cases}{{x}=\mathrm{5}}\\{{y}=\mathrm{4}}\end{cases} \\ $$$${si}\:{ab}=\mathrm{2} \\ $$$$\begin{cases}{{a}−{b}=\mathrm{3}}\\{\left({a}+{b}\right)^{\mathrm{2}} =\mathrm{17}}\end{cases}\:\Rightarrow\begin{cases}{{a}=\frac{\sqrt{\mathrm{17}}+\mathrm{3}}{\mathrm{2}}}\\{{b}=\frac{\sqrt{\mathrm{17}}−\mathrm{3}}{\mathrm{2}}}\end{cases}\:\:\Rightarrow\begin{cases}{{x}=\frac{\mathrm{13}}{\mathrm{2}}}\\{{y}=\frac{\mathrm{3}\sqrt{\mathrm{17}}}{\mathrm{2}}}\end{cases} \\ $$$$\left({x};{y}\right)=\left\{\left(\mathrm{5};\mathrm{4}\right);\left(\frac{\mathrm{13}}{\mathrm{2}};\frac{\mathrm{3}\sqrt{\mathrm{17}}}{\mathrm{2}}\right)\right\} \\ $$$$ \\ $$
Commented by mathdanisur last updated on 25/Sep/21
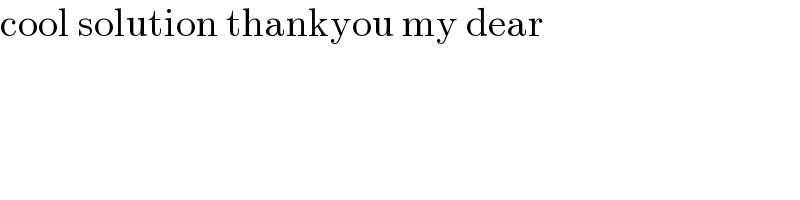
$$\mathrm{cool}\:\mathrm{solution}\:\mathrm{thankyou}\:\mathrm{my}\:\mathrm{dear} \\ $$
Commented by Tawa11 last updated on 25/Sep/21

$$\mathrm{Great}\:\mathrm{sirs} \\ $$
Answered by MJS_new last updated on 25/Sep/21
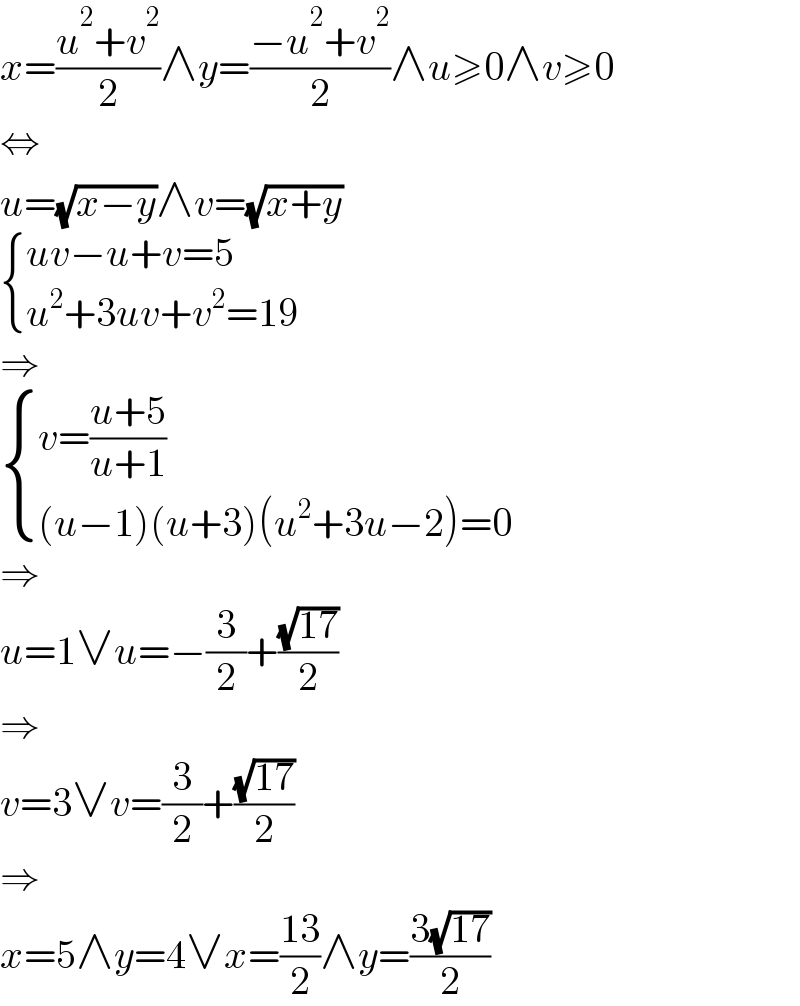
$${x}=\frac{{u}^{\mathrm{2}} +{v}^{\mathrm{2}} }{\mathrm{2}}\wedge{y}=\frac{−{u}^{\mathrm{2}} +{v}^{\mathrm{2}} }{\mathrm{2}}\wedge{u}\geqslant\mathrm{0}\wedge{v}\geqslant\mathrm{0} \\ $$$$\Leftrightarrow \\ $$$${u}=\sqrt{{x}−{y}}\wedge{v}=\sqrt{{x}+{y}} \\ $$$$\begin{cases}{{uv}−{u}+{v}=\mathrm{5}}\\{{u}^{\mathrm{2}} +\mathrm{3}{uv}+{v}^{\mathrm{2}} =\mathrm{19}}\end{cases} \\ $$$$\Rightarrow \\ $$$$\begin{cases}{{v}=\frac{{u}+\mathrm{5}}{{u}+\mathrm{1}}}\\{\left({u}−\mathrm{1}\right)\left({u}+\mathrm{3}\right)\left({u}^{\mathrm{2}} +\mathrm{3}{u}−\mathrm{2}\right)=\mathrm{0}}\end{cases} \\ $$$$\Rightarrow \\ $$$${u}=\mathrm{1}\vee{u}=−\frac{\mathrm{3}}{\mathrm{2}}+\frac{\sqrt{\mathrm{17}}}{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$${v}=\mathrm{3}\vee{v}=\frac{\mathrm{3}}{\mathrm{2}}+\frac{\sqrt{\mathrm{17}}}{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$${x}=\mathrm{5}\wedge{y}=\mathrm{4}\vee{x}=\frac{\mathrm{13}}{\mathrm{2}}\wedge{y}=\frac{\mathrm{3}\sqrt{\mathrm{17}}}{\mathrm{2}} \\ $$
Commented by mathdanisur last updated on 25/Sep/21
$$\mathrm{perfect}\:\mathrm{solution}\:\mathrm{thankyou}\:\mathrm{my}\:\mathrm{dear} \\ $$
