Question Number 166280 by Eulerian last updated on 17/Feb/22
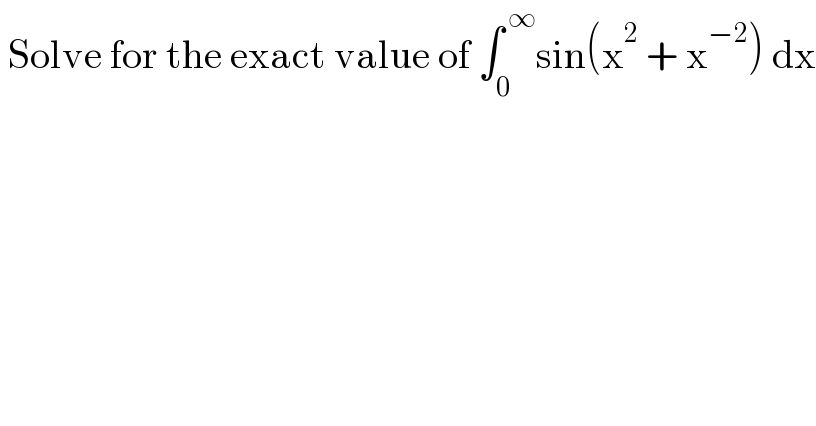
$$\:\mathrm{Solve}\:\mathrm{for}\:\mathrm{the}\:\mathrm{exact}\:\mathrm{value}\:\mathrm{of}\:\int_{\mathrm{0}} ^{\:\infty} \mathrm{sin}\left(\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{x}^{−\mathrm{2}} \right)\:\mathrm{dx} \\ $$
Answered by phanphuoc last updated on 17/Feb/22
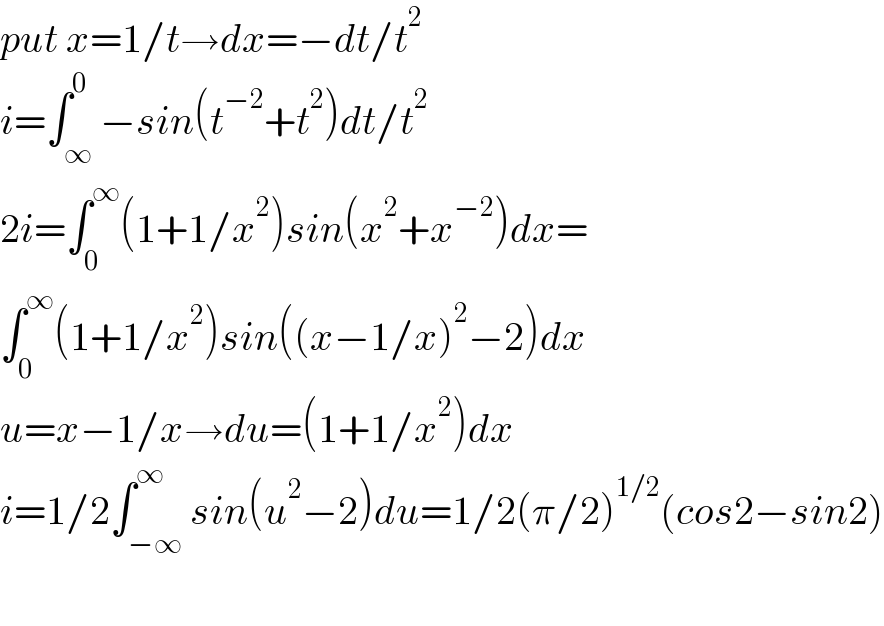
$${put}\:{x}=\mathrm{1}/{t}\rightarrow{dx}=−{dt}/{t}^{\mathrm{2}} \\ $$$${i}=\int_{\infty} ^{\mathrm{0}} −{sin}\left({t}^{−\mathrm{2}} +{t}^{\mathrm{2}} \right){dt}/{t}^{\mathrm{2}} \\ $$$$\mathrm{2}{i}=\int_{\mathrm{0}} ^{\infty} \left(\mathrm{1}+\mathrm{1}/{x}^{\mathrm{2}} \right){sin}\left({x}^{\mathrm{2}} +{x}^{−\mathrm{2}} \right){dx}= \\ $$$$\int_{\mathrm{0}} ^{\infty} \left(\mathrm{1}+\mathrm{1}/{x}^{\mathrm{2}} \right){sin}\left(\left({x}−\mathrm{1}/{x}\right)^{\mathrm{2}} −\mathrm{2}\right){dx} \\ $$$${u}={x}−\mathrm{1}/{x}\rightarrow{du}=\left(\mathrm{1}+\mathrm{1}/{x}^{\mathrm{2}} \right){dx} \\ $$$${i}=\mathrm{1}/\mathrm{2}\int_{−\infty} ^{\infty} {sin}\left({u}^{\mathrm{2}} −\mathrm{2}\right){du}=\mathrm{1}/\mathrm{2}\left(\pi/\mathrm{2}\right)^{\mathrm{1}/\mathrm{2}} \left({cos}\mathrm{2}−{sin}\mathrm{2}\right) \\ $$$$ \\ $$
Commented by Eulerian last updated on 18/Feb/22

$$\mathrm{No}\:\mathrm{sir},\:\mathrm{try}\:\mathrm{to}\:\mathrm{recheck}\:\mathrm{your}\:\mathrm{work}! \\ $$
Commented by MJS_new last updated on 18/Feb/22
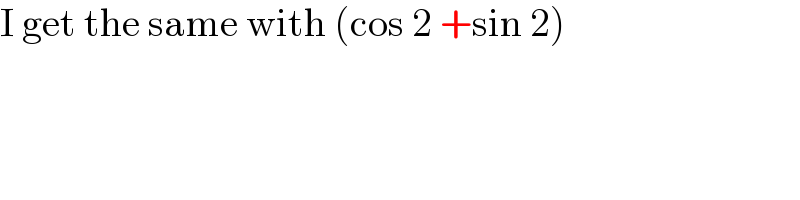
$$\mathrm{I}\:\mathrm{get}\:\mathrm{the}\:\mathrm{same}\:\mathrm{with}\:\left(\mathrm{cos}\:\mathrm{2}\:+\mathrm{sin}\:\mathrm{2}\right) \\ $$
Commented by Eulerian last updated on 19/Feb/22
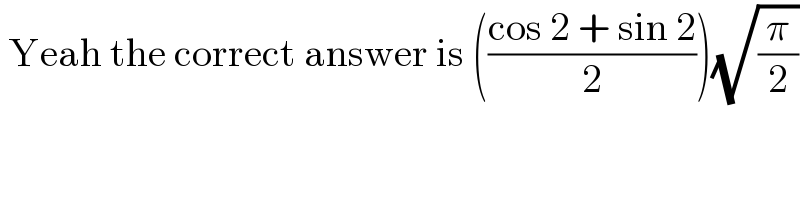
$$\:\mathrm{Yeah}\:\mathrm{the}\:\mathrm{correct}\:\mathrm{answer}\:\mathrm{is}\:\left(\frac{\mathrm{cos}\:\mathrm{2}\:+\:\mathrm{sin}\:\mathrm{2}}{\mathrm{2}}\right)\sqrt{\frac{\pi}{\mathrm{2}}} \\ $$
