Question Number 165778 by Odhiambojr last updated on 08/Feb/22

$$\mathrm{solve}\:\mathrm{for}\:\mathrm{the}\:\mathrm{values}\:\mathrm{of}\:\mathrm{m},\mathrm{n}\:\mathrm{and}\:\mathrm{l} \\ $$$$\mathrm{l}+\mathrm{m}+\mathrm{n}=\mathrm{0} \\ $$$$\mathrm{l}^{\mathrm{2}} +\mathrm{m}^{\mathrm{2}} −\mathrm{n}^{\mathrm{2}} =\mathrm{0} \\ $$
Answered by TheSupreme last updated on 08/Feb/22
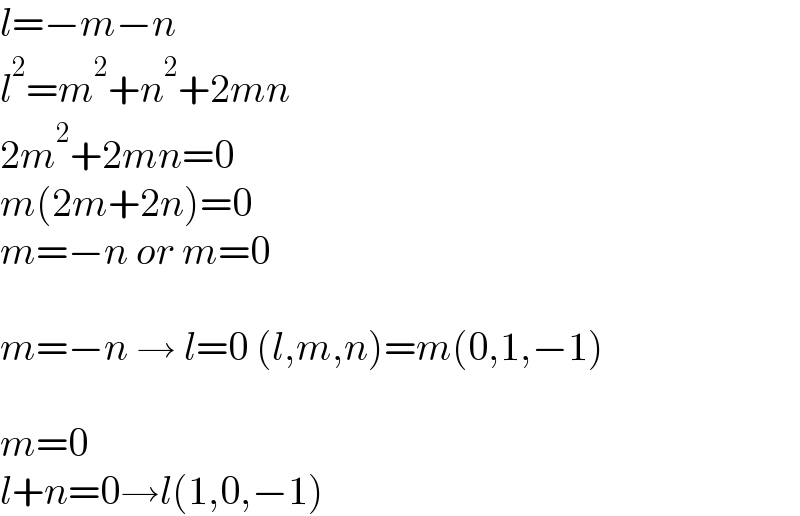
$${l}=−{m}−{n} \\ $$$${l}^{\mathrm{2}} ={m}^{\mathrm{2}} +{n}^{\mathrm{2}} +\mathrm{2}{mn} \\ $$$$\mathrm{2}{m}^{\mathrm{2}} +\mathrm{2}{mn}=\mathrm{0} \\ $$$${m}\left(\mathrm{2}{m}+\mathrm{2}{n}\right)=\mathrm{0} \\ $$$${m}=−{n}\:{or}\:{m}=\mathrm{0} \\ $$$$ \\ $$$${m}=−{n}\:\rightarrow\:{l}=\mathrm{0}\:\left({l},{m},{n}\right)={m}\left(\mathrm{0},\mathrm{1},−\mathrm{1}\right) \\ $$$$ \\ $$$${m}=\mathrm{0} \\ $$$${l}+{n}=\mathrm{0}\rightarrow{l}\left(\mathrm{1},\mathrm{0},−\mathrm{1}\right) \\ $$
