Question Number 176189 by Linton last updated on 14/Sep/22
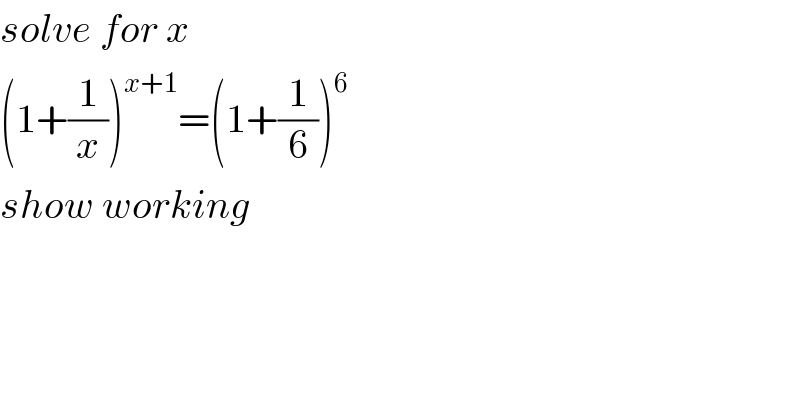
$${solve}\:{for}\:{x} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}+\mathrm{1}} =\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{6}}\right)^{\mathrm{6}} \\ $$$${show}\:{working} \\ $$
Answered by BaliramKumar last updated on 14/Sep/22
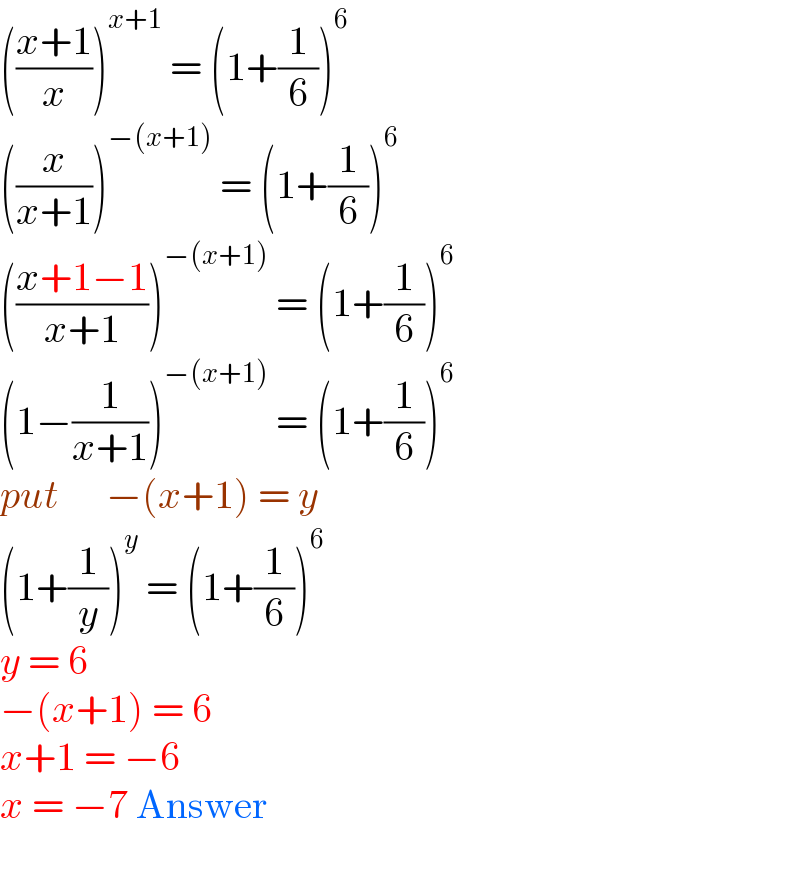
$$\left(\frac{{x}+\mathrm{1}}{{x}}\right)^{{x}+\mathrm{1}} \:=\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{6}}\right)^{\mathrm{6}} \\ $$$$\left(\frac{{x}}{{x}+\mathrm{1}}\right)^{−\left({x}+\mathrm{1}\right)} \:=\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{6}}\right)^{\mathrm{6}} \\ $$$$\left(\frac{{x}+\mathrm{1}−\mathrm{1}}{{x}+\mathrm{1}}\right)^{−\left({x}+\mathrm{1}\right)} \:=\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{6}}\right)^{\mathrm{6}} \\ $$$$\left(\mathrm{1}−\frac{\mathrm{1}}{{x}+\mathrm{1}}\right)^{−\left({x}+\mathrm{1}\right)} \:=\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{6}}\right)^{\mathrm{6}} \\ $$$${put}\:\:\:\:\:\:−\left({x}+\mathrm{1}\right)\:=\:{y} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{{y}}\right)^{{y}} \:=\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{6}}\right)^{\mathrm{6}} \\ $$$${y}\:=\:\mathrm{6} \\ $$$$−\left({x}+\mathrm{1}\right)\:=\:\mathrm{6} \\ $$$${x}+\mathrm{1}\:=\:−\mathrm{6} \\ $$$${x}\:=\:−\mathrm{7}\:\mathrm{Answer} \\ $$$$ \\ $$
