Menu Close

solve-for-x-1-3-x-x-1-gt-1-2-2-cos-2-x-cos-2-2x-cos-2-3x-1-3-x-2-p-2-x-2-1-x-p-R-

Tinku Tara 0 Comments
Pin




Question Number 54600 by behi83417@gmail.com last updated on 07/Feb/19
solve for: x 1) (√(3−x))+(√(x+1))>(1/2) 2) cos^2 x+cos^2 2x+cos^2 3x=1 3)(√(x^2 −p))+2(√(x^2 −1))=x [p∈R]
$$\boldsymbol{\mathrm{solve}}\:\boldsymbol{\mathrm{for}}:\:\boldsymbol{\mathrm{x}} \\ $$$$\left.\:\:\:\mathrm{1}\right)\:\sqrt{\mathrm{3}−\boldsymbol{\mathrm{x}}}+\sqrt{\boldsymbol{\mathrm{x}}+\mathrm{1}}>\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left.\:\:\:\:\mathrm{2}\right)\:\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \mathrm{2}\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \mathrm{3}\boldsymbol{\mathrm{x}}=\mathrm{1} \\ $$$$\left.\:\:\:\:\mathrm{3}\right)\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\boldsymbol{\mathrm{p}}}+\mathrm{2}\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{1}}=\boldsymbol{\mathrm{x}}\:\:\:\:\:\left[\boldsymbol{\mathrm{p}}\in\boldsymbol{\mathrm{R}}\right] \\ $$
Commented by maxmathsup by imad last updated on 07/Feb/19
1) we must have first 3−x≥0 and x+1 ≥0 ⇔ −1≤x≤3 (e) ⇔4 +2(√(3−x))(√(x+1))≥(1/4) ⇒2(√(3−x)) (√(x+1))≥ (1/4) −4 ⇒2(√(3−x))(√(x+1))≥((−7)/4) ⇒(√(3−x))(√(x+1))≥−(7/8) butthis inequality is true for all x∈[−1,3] ⇒ S=[−1,3] .
$$\left.\mathrm{1}\right)\:\:{we}\:{must}\:\:{have}\:{first}\:\:\mathrm{3}−{x}\geqslant\mathrm{0}\:{and}\:{x}+\mathrm{1}\:\geqslant\mathrm{0}\:\Leftrightarrow\:−\mathrm{1}\leqslant{x}\leqslant\mathrm{3} \\ $$$$\left({e}\right)\:\Leftrightarrow\mathrm{4}\:+\mathrm{2}\sqrt{\mathrm{3}−{x}}\sqrt{{x}+\mathrm{1}}\geqslant\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\mathrm{2}\sqrt{\mathrm{3}−{x}}\:\sqrt{{x}+\mathrm{1}}\geqslant\:\frac{\mathrm{1}}{\mathrm{4}}\:−\mathrm{4}\:\Rightarrow\mathrm{2}\sqrt{\mathrm{3}−{x}}\sqrt{{x}+\mathrm{1}}\geqslant\frac{−\mathrm{7}}{\mathrm{4}} \\ $$$$\Rightarrow\sqrt{\mathrm{3}−{x}}\sqrt{{x}+\mathrm{1}}\geqslant−\frac{\mathrm{7}}{\mathrm{8}}\:\:\:{butthis}\:{inequality}\:{is}\:{true}\:{for}\:{all}\:{x}\in\left[−\mathrm{1},\mathrm{3}\right]\:\Rightarrow \\ $$$${S}=\left[−\mathrm{1},\mathrm{3}\right]\:. \\ $$
Commented by maxmathsup by imad last updated on 07/Feb/19
2) (e) ⇔ ((1+cos(2x))/2) +((1+cos(4x))/2) + ((1+cos(6x))/2) =1 ⇔ 3 +cos(2x)+cos(4x)+cos(6x) =2 ⇒cos(2x)+cos(4x) +cos(6x)=−1 ⇒ but cosa +cosb =2cos(((a+b)/2))cos(((a−b)/2)) ⇒cos(2x)+cos(6x) =2cos(4x)cos(2x) ⇒2cos(4x)cos(2x) +cos(4x) =−1 ⇒ cos(4x)(2cos(2x)+1)=−1 ⇒(2cos^2 (2x)−1)(2cos(2x)+1) +1 =0 ⇒(2t^2 −1)(2t+1)+1 =0 with t =cos(2x) ⇒ 4t^3 +2t^2 −2t −1 +1 =0 ⇒t(4t^2 +2t−2) =0 ⇒2t(2t^2 +t−1)=0 ⇒t=0 or 2t^2 +t−1 =0 Δ =1−4(2)(−1) =9 ⇒t_1 =((−1+3)/4) =(1/2) and t_2 =−1 t=0 ⇒cos(2x)=0 ⇒2x =(π/2)+kπ ⇒x =(π/4) +((kπ)/2) (k∈Z) t=(1/2) ⇒cos(2x)=cos((π/3)) ⇒2x=(π/3) +2kπ or x =−(π/3) +2kπ ⇒ x =(π/6) +kπ or x =−(π/6) +kπ (k from Z) t=−1 ⇒cos(2x)=cosπ ⇒2x =(2k+1)π or 2x =(2k−1)π ⇒ x =(((2k+1)π)/2) or x =(((2k−1)π)/2) .
$$\left.\mathrm{2}\right)\:\left({e}\right)\:\Leftrightarrow\:\frac{\mathrm{1}+{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}\:+\frac{\mathrm{1}+{cos}\left(\mathrm{4}{x}\right)}{\mathrm{2}}\:+\:\frac{\mathrm{1}+{cos}\left(\mathrm{6}{x}\right)}{\mathrm{2}}\:=\mathrm{1}\:\Leftrightarrow \\ $$$$\mathrm{3}\:+{cos}\left(\mathrm{2}{x}\right)+{cos}\left(\mathrm{4}{x}\right)+{cos}\left(\mathrm{6}{x}\right)\:=\mathrm{2}\:\Rightarrow{cos}\left(\mathrm{2}{x}\right)+{cos}\left(\mathrm{4}{x}\right)\:+{cos}\left(\mathrm{6}{x}\right)=−\mathrm{1}\:\Rightarrow \\ $$$${but}\:{cosa}\:\:+{cosb}\:=\mathrm{2}{cos}\left(\frac{{a}+{b}}{\mathrm{2}}\right){cos}\left(\frac{{a}−{b}}{\mathrm{2}}\right)\:\Rightarrow{cos}\left(\mathrm{2}{x}\right)+{cos}\left(\mathrm{6}{x}\right) \\ $$$$=\mathrm{2}{cos}\left(\mathrm{4}{x}\right){cos}\left(\mathrm{2}{x}\right)\:\Rightarrow\mathrm{2}{cos}\left(\mathrm{4}{x}\right){cos}\left(\mathrm{2}{x}\right)\:+{cos}\left(\mathrm{4}{x}\right)\:=−\mathrm{1}\:\Rightarrow \\ $$$${cos}\left(\mathrm{4}{x}\right)\left(\mathrm{2}{cos}\left(\mathrm{2}{x}\right)+\mathrm{1}\right)=−\mathrm{1}\:\Rightarrow\left(\mathrm{2}{cos}^{\mathrm{2}} \left(\mathrm{2}{x}\right)−\mathrm{1}\right)\left(\mathrm{2}{cos}\left(\mathrm{2}{x}\right)+\mathrm{1}\right)\:+\mathrm{1}\:=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{2}{t}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{2}{t}+\mathrm{1}\right)+\mathrm{1}\:=\mathrm{0}\:\:{with}\:{t}\:={cos}\left(\mathrm{2}{x}\right)\:\Rightarrow \\ $$$$\mathrm{4}{t}^{\mathrm{3}} \:+\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2}{t}\:−\mathrm{1}\:+\mathrm{1}\:=\mathrm{0}\:\Rightarrow{t}\left(\mathrm{4}{t}^{\mathrm{2}} \:+\mathrm{2}{t}−\mathrm{2}\right)\:=\mathrm{0}\:\Rightarrow\mathrm{2}{t}\left(\mathrm{2}{t}^{\mathrm{2}} \:+{t}−\mathrm{1}\right)=\mathrm{0}\:\Rightarrow{t}=\mathrm{0}\:{or} \\ $$$$\mathrm{2}{t}^{\mathrm{2}} \:+{t}−\mathrm{1}\:=\mathrm{0} \\ $$$$\Delta\:=\mathrm{1}−\mathrm{4}\left(\mathrm{2}\right)\left(−\mathrm{1}\right)\:=\mathrm{9}\:\Rightarrow{t}_{\mathrm{1}} =\frac{−\mathrm{1}+\mathrm{3}}{\mathrm{4}}\:=\frac{\mathrm{1}}{\mathrm{2}}\:{and}\:{t}_{\mathrm{2}} =−\mathrm{1} \\ $$$${t}=\mathrm{0}\:\Rightarrow{cos}\left(\mathrm{2}{x}\right)=\mathrm{0}\:\Rightarrow\mathrm{2}{x}\:=\frac{\pi}{\mathrm{2}}+{k}\pi\:\Rightarrow{x}\:=\frac{\pi}{\mathrm{4}}\:+\frac{{k}\pi}{\mathrm{2}}\:\:\left({k}\in{Z}\right) \\ $$$${t}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{cos}\left(\mathrm{2}{x}\right)={cos}\left(\frac{\pi}{\mathrm{3}}\right)\:\Rightarrow\mathrm{2}{x}=\frac{\pi}{\mathrm{3}}\:+\mathrm{2}{k}\pi\:{or}\:{x}\:=−\frac{\pi}{\mathrm{3}}\:+\mathrm{2}{k}\pi\:\Rightarrow \\ $$$${x}\:=\frac{\pi}{\mathrm{6}}\:+{k}\pi\:{or}\:{x}\:=−\frac{\pi}{\mathrm{6}}\:+{k}\pi\:\left({k}\:{from}\:{Z}\right) \\ $$$${t}=−\mathrm{1}\:\Rightarrow{cos}\left(\mathrm{2}{x}\right)={cos}\pi\:\Rightarrow\mathrm{2}{x}\:=\left(\mathrm{2}{k}+\mathrm{1}\right)\pi\:{or}\:\mathrm{2}{x}\:=\left(\mathrm{2}{k}−\mathrm{1}\right)\pi\:\Rightarrow \\ $$$${x}\:=\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{2}}\:{or}\:{x}\:=\frac{\left(\mathrm{2}{k}−\mathrm{1}\right)\pi}{\mathrm{2}}\:\:. \\ $$
Answered by MJS last updated on 07/Feb/19
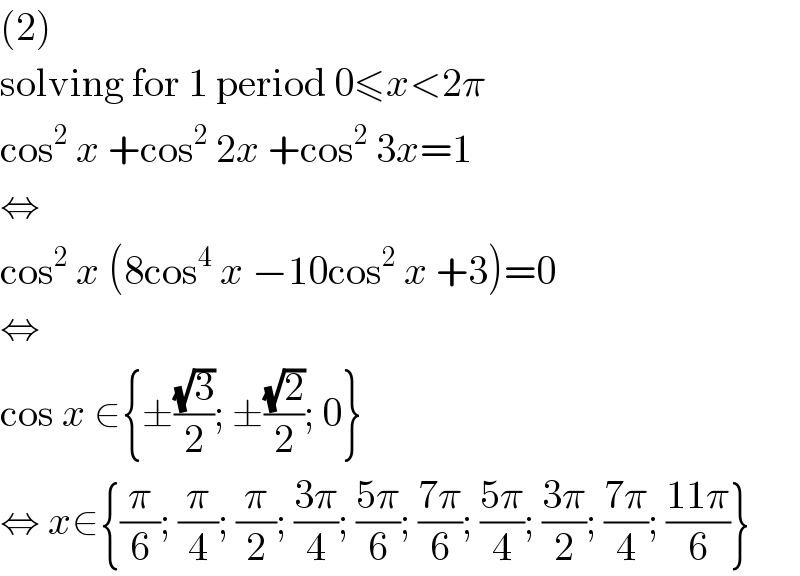
(2) solving for 1 period 0≤x<2π cos^2 x +cos^2 2x +cos^2 3x=1 ⇔ cos^2 x (8cos^4 x −10cos^2 x +3)=0 ⇔ cos x ∈{±((√3)/2); ±((√2)/2); 0} ⇔ x∈{(π/6); (π/4); (π/2); ((3π)/4); ((5π)/6); ((7π)/6); ((5π)/4); ((3π)/2); ((7π)/4); ((11π)/6)}
$$\left(\mathrm{2}\right) \\ $$$$\mathrm{solving}\:\mathrm{for}\:\mathrm{1}\:\mathrm{period}\:\mathrm{0}\leqslant{x}<\mathrm{2}\pi \\ $$$$\mathrm{cos}^{\mathrm{2}} \:{x}\:+\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}{x}\:+\mathrm{cos}^{\mathrm{2}} \:\mathrm{3}{x}=\mathrm{1} \\ $$$$\Leftrightarrow \\ $$$$\mathrm{cos}^{\mathrm{2}} \:{x}\:\left(\mathrm{8cos}^{\mathrm{4}} \:{x}\:−\mathrm{10cos}^{\mathrm{2}} \:{x}\:+\mathrm{3}\right)=\mathrm{0} \\ $$$$\Leftrightarrow \\ $$$$\mathrm{cos}\:{x}\:\in\left\{\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}};\:\pm\frac{\sqrt{\mathrm{2}}}{\mathrm{2}};\:\mathrm{0}\right\} \\ $$$$\Leftrightarrow\:{x}\in\left\{\frac{\pi}{\mathrm{6}};\:\frac{\pi}{\mathrm{4}};\:\frac{\pi}{\mathrm{2}};\:\frac{\mathrm{3}\pi}{\mathrm{4}};\:\frac{\mathrm{5}\pi}{\mathrm{6}};\:\frac{\mathrm{7}\pi}{\mathrm{6}};\:\frac{\mathrm{5}\pi}{\mathrm{4}};\:\frac{\mathrm{3}\pi}{\mathrm{2}};\:\frac{\mathrm{7}\pi}{\mathrm{4}};\:\frac{\mathrm{11}\pi}{\mathrm{6}}\right\} \\ $$
Answered by MJS last updated on 07/Feb/19
(3) squaring 4(√(x^2 −1))(√(x^2 −p))+5x^2 −p−4=x^2 4(√(x^2 −1))(√(x^2 −p))=−4x^2 +p+4 squaring again and transforming x^2 =(((p−4)^2 )/(8(2−p))) ≥0 ⇒ p∈]−∞; 2[∪{4} x=±(((p−4)(√2))/(4(√(2−p)))) but only one solution solves the original eq trying we find x=(((4−p)(√2))/(4(√(2−p)))) but only if 0≤p≤(4/3)
$$\left(\mathrm{3}\right) \\ $$$$\mathrm{squaring} \\ $$$$\mathrm{4}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\sqrt{{x}^{\mathrm{2}} −{p}}+\mathrm{5}{x}^{\mathrm{2}} −{p}−\mathrm{4}={x}^{\mathrm{2}} \\ $$$$\mathrm{4}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\sqrt{{x}^{\mathrm{2}} −{p}}=−\mathrm{4}{x}^{\mathrm{2}} +{p}+\mathrm{4} \\ $$$$\mathrm{squaring}\:\mathrm{again}\:\mathrm{and}\:\mathrm{transforming} \\ $$$$\left.{x}^{\mathrm{2}} =\frac{\left({p}−\mathrm{4}\right)^{\mathrm{2}} }{\mathrm{8}\left(\mathrm{2}−{p}\right)}\:\geqslant\mathrm{0}\:\Rightarrow\:{p}\in\right]−\infty;\:\mathrm{2}\left[\cup\left\{\mathrm{4}\right\}\right. \\ $$$${x}=\pm\frac{\left({p}−\mathrm{4}\right)\sqrt{\mathrm{2}}}{\mathrm{4}\sqrt{\mathrm{2}−{p}}} \\ $$$$\mathrm{but}\:\mathrm{only}\:\mathrm{one}\:\mathrm{solution}\:\mathrm{solves}\:\mathrm{the}\:\mathrm{original}\:\mathrm{eq} \\ $$$$\mathrm{trying}\:\mathrm{we}\:\mathrm{find} \\ $$$${x}=\frac{\left(\mathrm{4}−{p}\right)\sqrt{\mathrm{2}}}{\mathrm{4}\sqrt{\mathrm{2}−{p}}}\:\mathrm{but}\:\mathrm{only}\:\mathrm{if}\:\mathrm{0}\leqslant{p}\leqslant\frac{\mathrm{4}}{\mathrm{3}} \\ $$
Commented by behi83417@gmail.com last updated on 08/Feb/19
thank you very much sir Abdo and sir MJS.i cant recive notifications from app any more.
$${thank}\:{you}\:{very}\:{much}\:{sir}\:{Abdo}\:{and}\:{sir} \\ $$$${MJS}.{i}\:{cant}\:{recive}\:{notifications}\:{from} \\ $$$${app}\:{any}\:{more}. \\ $$
Commented by MJS last updated on 08/Feb/19
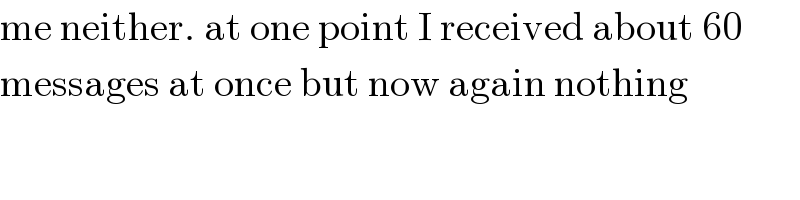
me neither. at one point I received about 60 messages at once but now again nothing
$$\mathrm{me}\:\mathrm{neither}.\:\mathrm{at}\:\mathrm{one}\:\mathrm{point}\:\mathrm{I}\:\mathrm{received}\:\mathrm{about}\:\mathrm{60} \\ $$$$\mathrm{messages}\:\mathrm{at}\:\mathrm{once}\:\mathrm{but}\:\mathrm{now}\:\mathrm{again}\:\mathrm{nothing} \\ $$
Commented by rahul 19 last updated on 08/Feb/19
me neither :\
$${me}\:{neither}\::\backslash \\ $$
Commented by mr W last updated on 08/Feb/19
me tooooo!
$${me}\:{tooooo}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *