Question Number 175443 by Linton last updated on 30/Aug/22

$${solve}\:{for}\:{x} \\ $$$$\mathrm{16}^{{x}} +\mathrm{20}^{{x}} =\:\mathrm{25}^{{x}} \\ $$
Answered by Ar Brandon last updated on 30/Aug/22
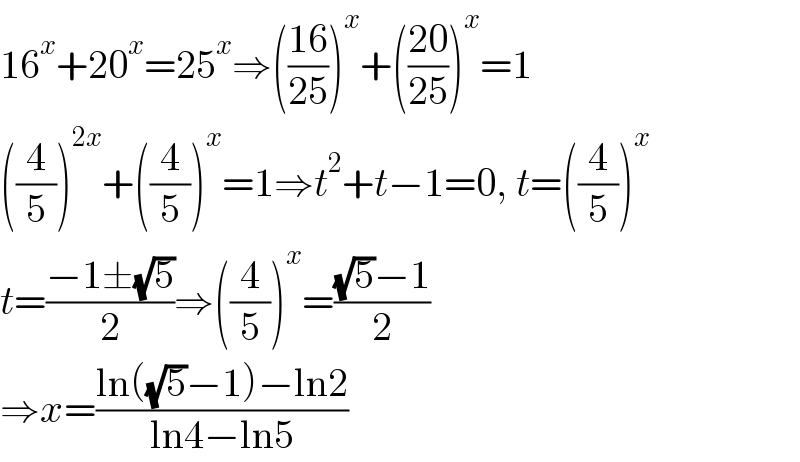
$$\mathrm{16}^{{x}} +\mathrm{20}^{{x}} =\mathrm{25}^{{x}} \Rightarrow\left(\frac{\mathrm{16}}{\mathrm{25}}\right)^{{x}} +\left(\frac{\mathrm{20}}{\mathrm{25}}\right)^{{x}} =\mathrm{1} \\ $$$$\left(\frac{\mathrm{4}}{\mathrm{5}}\right)^{\mathrm{2}{x}} +\left(\frac{\mathrm{4}}{\mathrm{5}}\right)^{{x}} =\mathrm{1}\Rightarrow{t}^{\mathrm{2}} +{t}−\mathrm{1}=\mathrm{0},\:{t}=\left(\frac{\mathrm{4}}{\mathrm{5}}\right)^{{x}} \\ $$$${t}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}\Rightarrow\left(\frac{\mathrm{4}}{\mathrm{5}}\right)^{{x}} =\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{ln}\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)−\mathrm{ln2}}{\mathrm{ln4}−\mathrm{ln5}} \\ $$
Commented by peter frank last updated on 31/Aug/22

$$\mathrm{thanks} \\ $$
