Question Number 50698 by Cheyboy last updated on 19/Dec/18
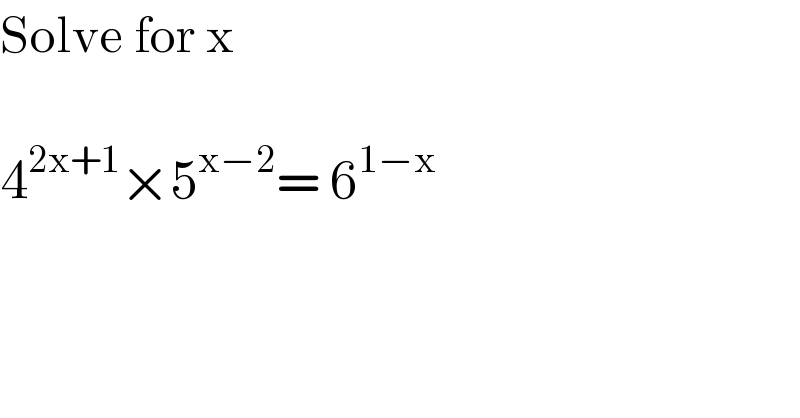
$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{x} \\ $$$$ \\ $$$$\mathrm{4}^{\mathrm{2x}+\mathrm{1}} ×\mathrm{5}^{\mathrm{x}−\mathrm{2}} =\:\mathrm{6}^{\mathrm{1}−\mathrm{x}} \\ $$
Answered by MJS last updated on 19/Dec/18
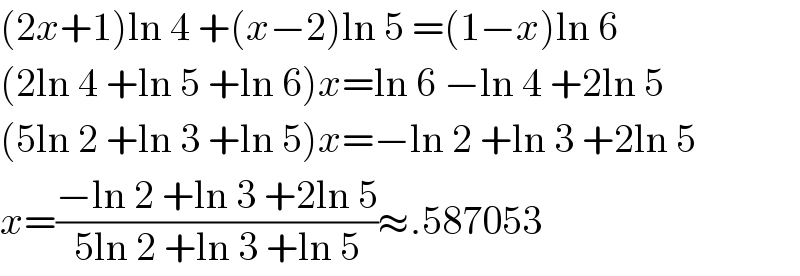
$$\left(\mathrm{2}{x}+\mathrm{1}\right)\mathrm{ln}\:\mathrm{4}\:+\left({x}−\mathrm{2}\right)\mathrm{ln}\:\mathrm{5}\:=\left(\mathrm{1}−{x}\right)\mathrm{ln}\:\mathrm{6} \\ $$$$\left(\mathrm{2ln}\:\mathrm{4}\:+\mathrm{ln}\:\mathrm{5}\:+\mathrm{ln}\:\mathrm{6}\right){x}=\mathrm{ln}\:\mathrm{6}\:−\mathrm{ln}\:\mathrm{4}\:+\mathrm{2ln}\:\mathrm{5} \\ $$$$\left(\mathrm{5ln}\:\mathrm{2}\:+\mathrm{ln}\:\mathrm{3}\:+\mathrm{ln}\:\mathrm{5}\right){x}=−\mathrm{ln}\:\mathrm{2}\:+\mathrm{ln}\:\mathrm{3}\:+\mathrm{2ln}\:\mathrm{5} \\ $$$${x}=\frac{−\mathrm{ln}\:\mathrm{2}\:+\mathrm{ln}\:\mathrm{3}\:+\mathrm{2ln}\:\mathrm{5}}{\mathrm{5ln}\:\mathrm{2}\:+\mathrm{ln}\:\mathrm{3}\:+\mathrm{ln}\:\mathrm{5}}\approx.\mathrm{587053} \\ $$
Commented by Cheyboy last updated on 19/Dec/18

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir}\:\mathrm{Godblesd}\:\mathrm{you} \\ $$$$ \\ $$
