Question Number 62998 by mr W last updated on 27/Jun/19
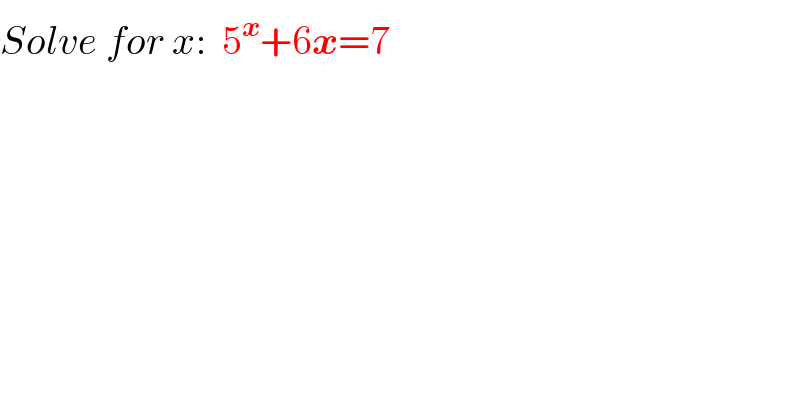
$${Solve}\:{for}\:{x}:\:\:\mathrm{5}^{\boldsymbol{{x}}} +\mathrm{6}\boldsymbol{{x}}=\mathrm{7} \\ $$
Commented by mr W last updated on 27/Jun/19

$${Equation}\:{like}\:{this}\:{can}\:{be}\:{solved}\:{using} \\ $$$${Lambert}\:{W}\:{function}\:{as}\:{following}: \\ $$
Commented by mr W last updated on 27/Jun/19
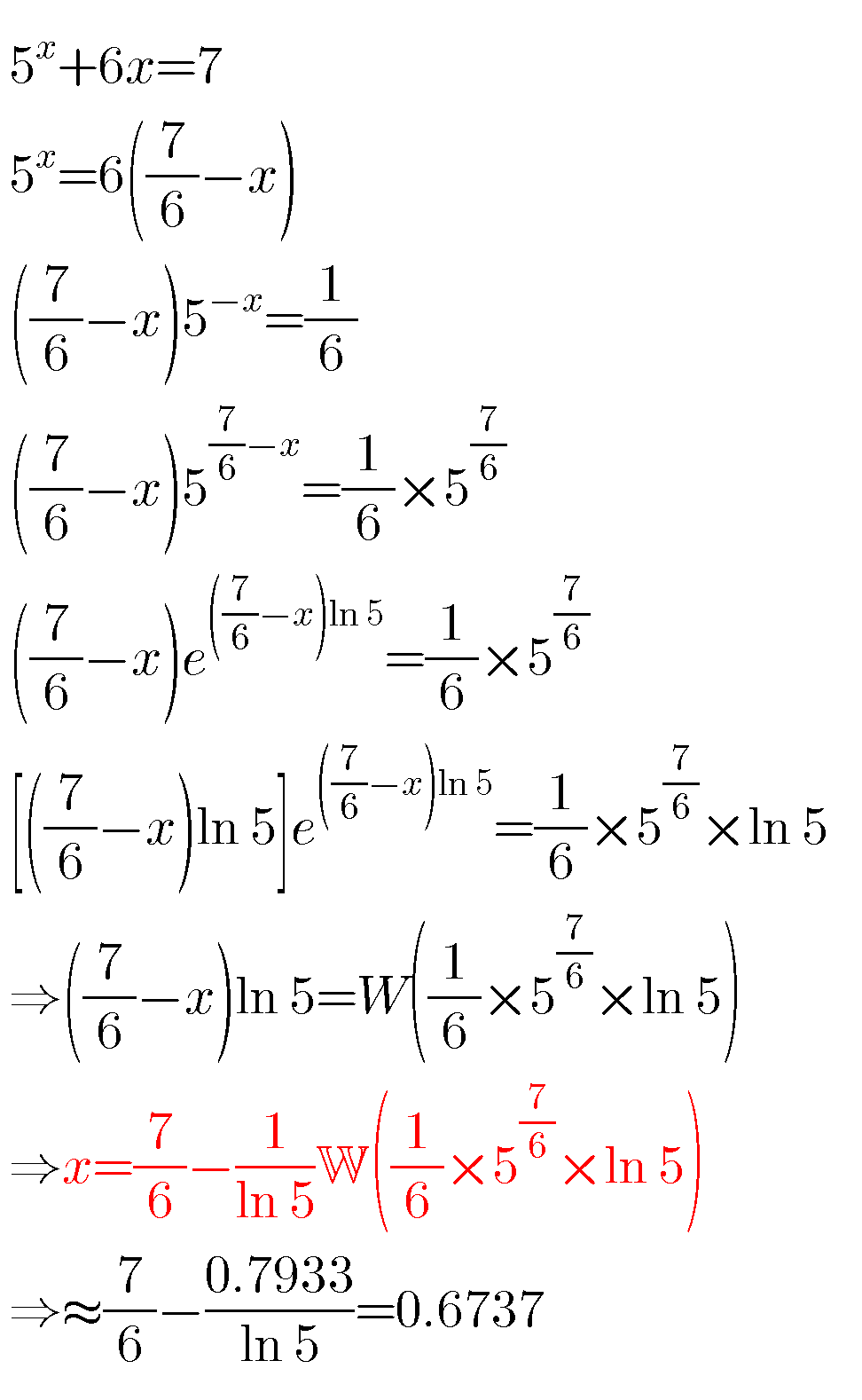
Commented by Tawa1 last updated on 27/Jun/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by Tawa1 last updated on 28/Jun/19
![(1) Can we evaluate something like this sir: W[− ln(2)] (2) And is there anything like W_n (ln 2), n ∈ Z. Does that mean we can evaluate something like this: W_2 (ln 2)](https://www.tinkutara.com/question/Q63028.png)
$$\left(\mathrm{1}\right)\:\mathrm{Can}\:\mathrm{we}\:\mathrm{evaluate}\:\mathrm{something}\:\mathrm{like}\:\mathrm{this}\:\mathrm{sir}:\:\:\:\:\:\mathrm{W}\left[−\:\mathrm{ln}\left(\mathrm{2}\right)\right] \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\:\mathrm{And}\:\mathrm{is}\:\mathrm{there}\:\mathrm{anything}\:\mathrm{like}\:\:\:\:\:\mathrm{W}_{\mathrm{n}} \left(\mathrm{ln}\:\mathrm{2}\right),\:\:\mathrm{n}\:\in\:\mathbb{Z}. \\ $$$$\mathrm{Does}\:\mathrm{that}\:\mathrm{mean}\:\mathrm{we}\:\mathrm{can}\:\mathrm{evaluate}\:\mathrm{something}\:\mathrm{like}\:\mathrm{this}:\:\:\mathrm{W}_{\mathrm{2}} \left(\mathrm{ln}\:\mathrm{2}\right) \\ $$
Commented by Cheyboy last updated on 28/Jun/19

$${I}\:{don}'{t}\:{so}\:{sir}\:{you}\:{need}\:{an}\:{online}\:{calculator} \\ $$$${for}\:{that} \\ $$
Commented by Cheyboy last updated on 28/Jun/19

$${Welldon}\:{Mr}\:{W}\:\:{Nice}\:{working} \\ $$
Commented by mr W last updated on 28/Jun/19

$${To}\:{Tawa}\:\mathrm{1}\:{sir}: \\ $$$${some}\:{special}\:{values}\:{exist},\:{see}\:{picture}. \\ $$$${other}\:{values}\:{must}\:{be}\:{calculated}. \\ $$$${W}\left(−\sqrt{\mathrm{2}}\right)\:{is}\:{no}\:{real}\:{value}. \\ $$$${i}\:{don}'{t}\:{know}\:{what}\:{you}\:{mean}\:{with}\:{W}_{{n}} . \\ $$
Commented by mr W last updated on 28/Jun/19
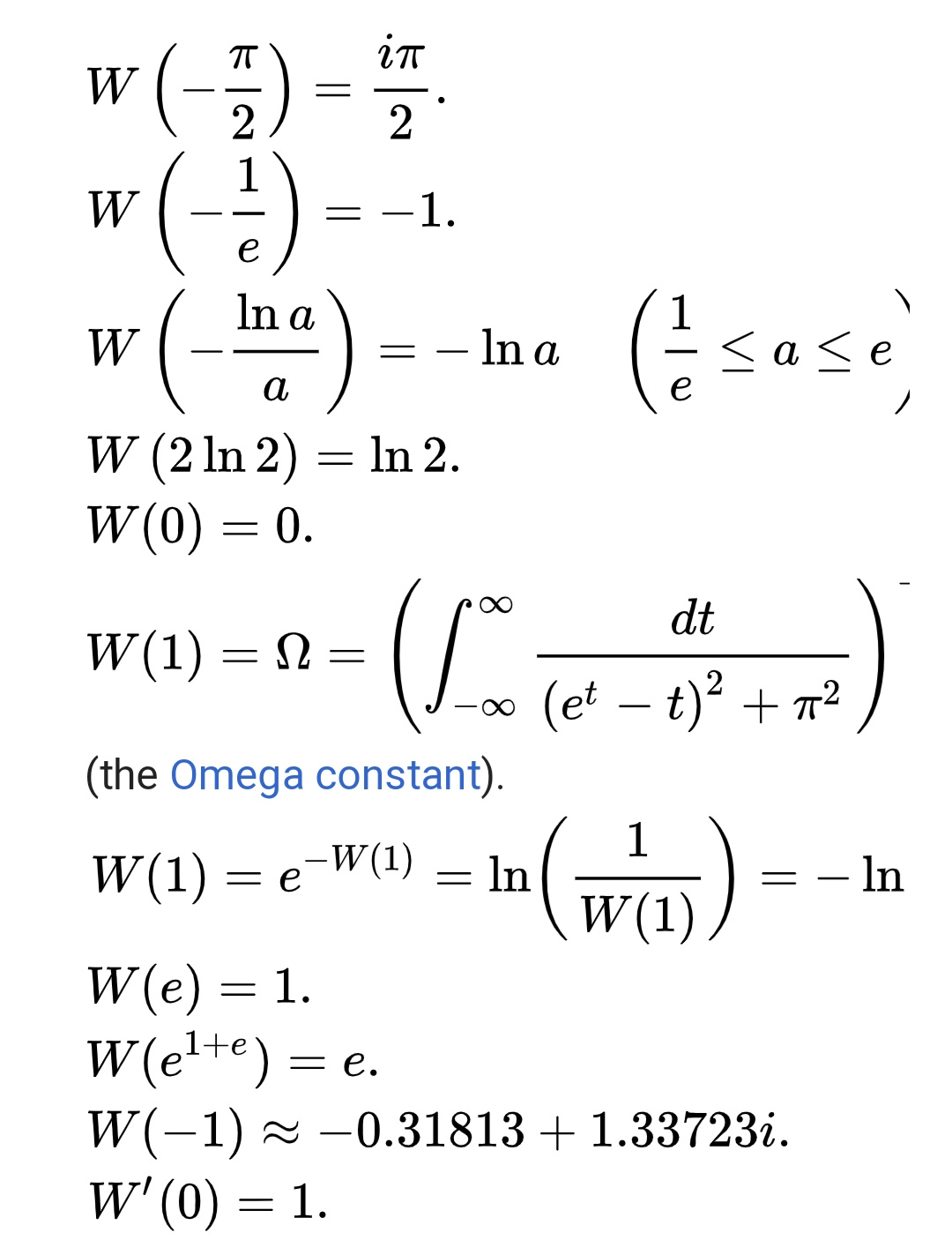
Commented by Tawa1 last updated on 28/Jun/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by Tawa1 last updated on 30/Jun/19
$$\mathrm{Sir},\:\:\mathrm{help}\:\mathrm{me}\:\mathrm{see}\:\mathrm{this}.\:\:\:\:\:\:\: \\ $$
Commented by Tawa1 last updated on 30/Jun/19

$$\mathrm{Sir},\:\:\mathrm{help}\:\mathrm{me}\:\mathrm{see}\:\mathrm{this}.\:\:\:\:\:\:\:\mathrm{x}^{\mathrm{x}^{\mathrm{x}} } \:\:=\:\:\mathrm{16} \\ $$
Commented by Tawa1 last updated on 30/Jun/19

$$\mathrm{Am}\:\mathrm{sorry}\:\mathrm{for}\:\mathrm{taking}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir} \\ $$
