Question Number 14559 by tawa tawa last updated on 02/Jun/17
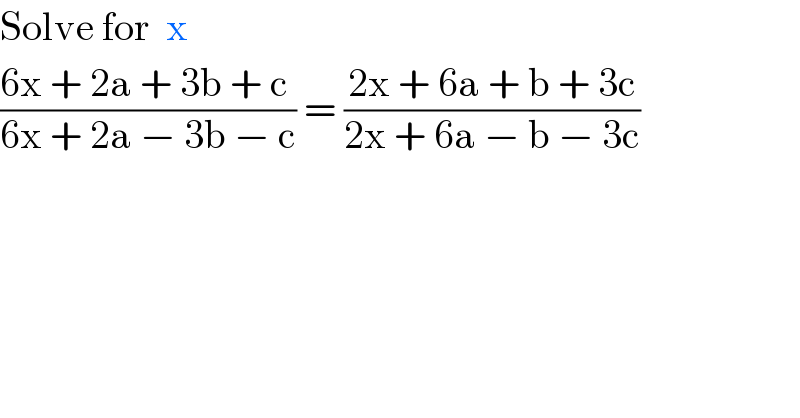
$$\mathrm{Solve}\:\mathrm{for}\:\:\mathrm{x} \\ $$$$\frac{\mathrm{6x}\:+\:\mathrm{2a}\:+\:\mathrm{3b}\:+\:\mathrm{c}\:}{\mathrm{6x}\:+\:\mathrm{2a}\:−\:\mathrm{3b}\:−\:\mathrm{c}}\:=\:\frac{\mathrm{2x}\:+\:\mathrm{6a}\:+\:\mathrm{b}\:+\:\mathrm{3c}}{\mathrm{2x}\:+\:\mathrm{6a}\:−\:\mathrm{b}\:−\:\mathrm{3c}} \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 02/Jun/17
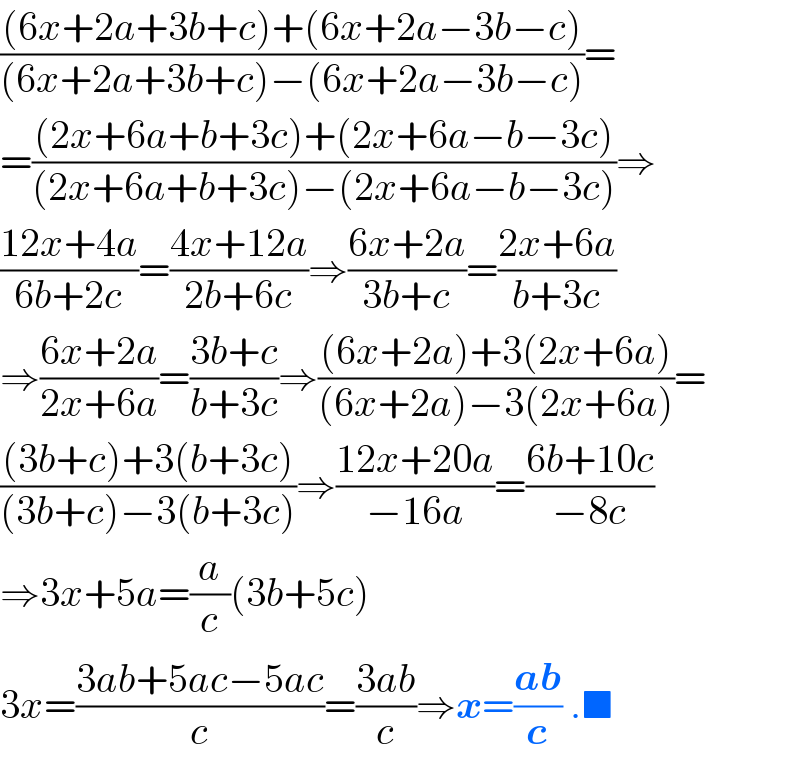
$$\frac{\left(\mathrm{6}{x}+\mathrm{2}{a}+\mathrm{3}{b}+{c}\right)+\left(\mathrm{6}{x}+\mathrm{2}{a}−\mathrm{3}{b}−{c}\right)}{\left(\mathrm{6}{x}+\mathrm{2}{a}+\mathrm{3}{b}+{c}\right)−\left(\mathrm{6}{x}+\mathrm{2}{a}−\mathrm{3}{b}−{c}\right)}= \\ $$$$=\frac{\left(\mathrm{2}{x}+\mathrm{6}{a}+{b}+\mathrm{3}{c}\right)+\left(\mathrm{2}{x}+\mathrm{6}{a}−{b}−\mathrm{3}{c}\right)}{\left(\mathrm{2}{x}+\mathrm{6}{a}+{b}+\mathrm{3}{c}\right)−\left(\mathrm{2}{x}+\mathrm{6}{a}−{b}−\mathrm{3}{c}\right)}\Rightarrow \\ $$$$\frac{\mathrm{12}{x}+\mathrm{4}{a}}{\mathrm{6}{b}+\mathrm{2}{c}}=\frac{\mathrm{4}{x}+\mathrm{12}{a}}{\mathrm{2}{b}+\mathrm{6}{c}}\Rightarrow\frac{\mathrm{6}{x}+\mathrm{2}{a}}{\mathrm{3}{b}+{c}}=\frac{\mathrm{2}{x}+\mathrm{6}{a}}{{b}+\mathrm{3}{c}} \\ $$$$\Rightarrow\frac{\mathrm{6}{x}+\mathrm{2}{a}}{\mathrm{2}{x}+\mathrm{6}{a}}=\frac{\mathrm{3}{b}+{c}}{{b}+\mathrm{3}{c}}\Rightarrow\frac{\left(\mathrm{6}{x}+\mathrm{2}{a}\right)+\mathrm{3}\left(\mathrm{2}{x}+\mathrm{6}{a}\right)}{\left(\mathrm{6}{x}+\mathrm{2}{a}\right)−\mathrm{3}\left(\mathrm{2}{x}+\mathrm{6}{a}\right)}= \\ $$$$\frac{\left(\mathrm{3}{b}+{c}\right)+\mathrm{3}\left({b}+\mathrm{3}{c}\right)}{\left(\mathrm{3}{b}+{c}\right)−\mathrm{3}\left({b}+\mathrm{3}{c}\right)}\Rightarrow\frac{\mathrm{12}{x}+\mathrm{20}{a}}{−\mathrm{16}{a}}=\frac{\mathrm{6}{b}+\mathrm{10}{c}}{−\mathrm{8}{c}} \\ $$$$\Rightarrow\mathrm{3}{x}+\mathrm{5}{a}=\frac{{a}}{{c}}\left(\mathrm{3}{b}+\mathrm{5}{c}\right) \\ $$$$\mathrm{3}{x}=\frac{\mathrm{3}{ab}+\mathrm{5}{ac}−\mathrm{5}{ac}}{{c}}=\frac{\mathrm{3}{ab}}{{c}}\Rightarrow\boldsymbol{{x}}=\frac{\boldsymbol{{ab}}}{\boldsymbol{{c}}}\:.\blacksquare \\ $$
Commented by Tinkutara last updated on 02/Jun/17
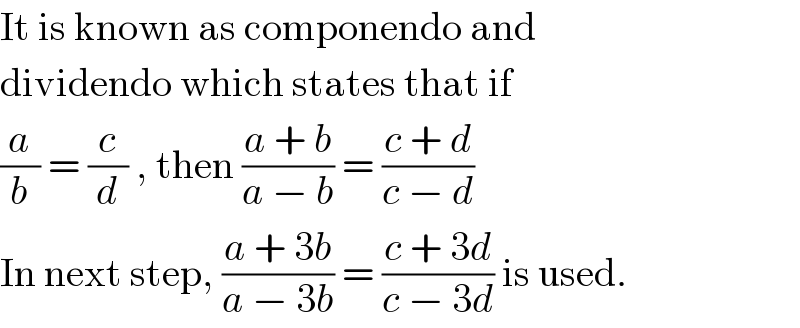
$$\mathrm{It}\:\mathrm{is}\:\mathrm{known}\:\mathrm{as}\:\mathrm{componendo}\:\mathrm{and} \\ $$$$\mathrm{dividendo}\:\mathrm{which}\:\mathrm{states}\:\mathrm{that}\:\mathrm{if} \\ $$$$\frac{{a}}{{b}}\:=\:\frac{{c}}{{d}}\:,\:\mathrm{then}\:\frac{{a}\:+\:{b}}{{a}\:−\:{b}}\:=\:\frac{{c}\:+\:{d}}{{c}\:−\:{d}} \\ $$$$\mathrm{In}\:\mathrm{next}\:\mathrm{step},\:\frac{{a}\:+\:\mathrm{3}{b}}{{a}\:−\:\mathrm{3}{b}}\:=\:\frac{{c}\:+\:\mathrm{3}{d}}{{c}\:−\:\mathrm{3}{d}}\:\mathrm{is}\:\mathrm{used}. \\ $$
Commented by tawa tawa last updated on 02/Jun/17

$$\mathrm{Wow},\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$
Commented by tawa tawa last updated on 02/Jun/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by tawa tawa last updated on 02/Jun/17

$$\mathrm{Sir},\:\mathrm{i}\:\mathrm{don}'\mathrm{t}\:\mathrm{really}\:\mathrm{understand}\:\mathrm{the}\:\mathrm{first}\:\mathrm{step}.\:\mathrm{please}\:\mathrm{what}\:\mathrm{did}\:\mathrm{you}\:\mathrm{do}\:\mathrm{sir}. \\ $$
Commented by mrW1 last updated on 02/Jun/17
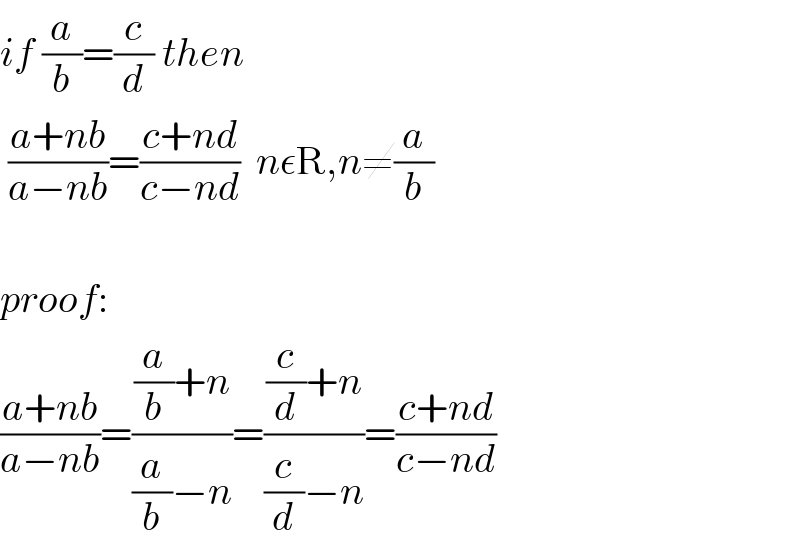
$${if}\:\frac{{a}}{{b}}=\frac{{c}}{{d}}\:{then} \\ $$$$\:\frac{{a}+{nb}}{{a}−{nb}}=\frac{{c}+{nd}}{{c}−{nd}}\:\:{n}\epsilon\mathrm{R},{n}\neq\frac{{a}}{{b}} \\ $$$$ \\ $$$${proof}: \\ $$$$\frac{{a}+{nb}}{{a}−{nb}}=\frac{\frac{{a}}{{b}}+{n}}{\frac{{a}}{{b}}−{n}}=\frac{\frac{{c}}{{d}}+{n}}{\frac{{c}}{{d}}−{n}}=\frac{{c}+{nd}}{{c}−{nd}} \\ $$
