Question Number 168247 by Mastermind last updated on 07/Apr/22

$${Solve}\:{for}\:{x} \\ $$$$\frac{\mathrm{8}^{{x}} +\mathrm{27}^{{x}} }{\mathrm{12}^{{x}} +\mathrm{18}^{{x}} }=\frac{\mathrm{7}}{\mathrm{6}} \\ $$$$ \\ $$$${Mastermind} \\ $$
Answered by MJS_new last updated on 07/Apr/22
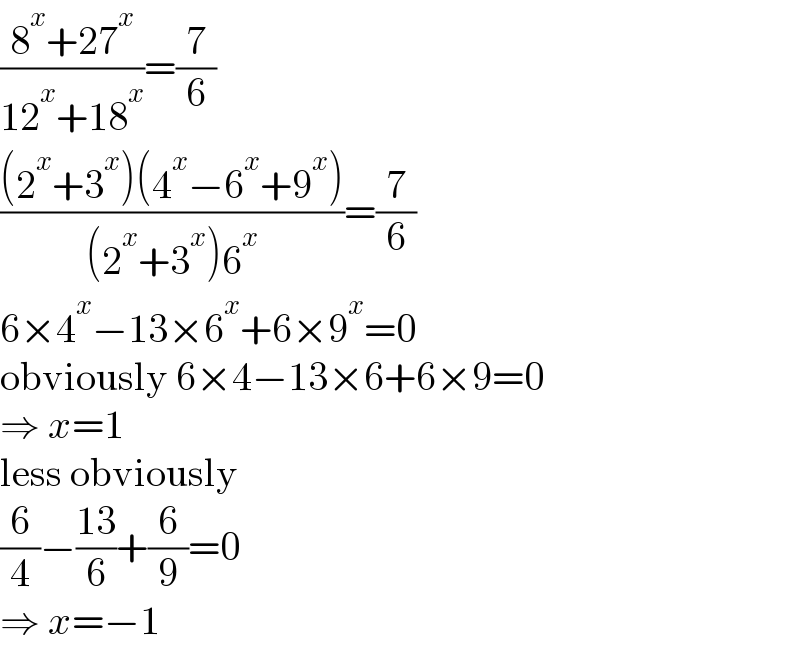
$$\frac{\mathrm{8}^{{x}} +\mathrm{27}^{{x}} }{\mathrm{12}^{{x}} +\mathrm{18}^{{x}} }=\frac{\mathrm{7}}{\mathrm{6}} \\ $$$$\frac{\left(\mathrm{2}^{{x}} +\mathrm{3}^{{x}} \right)\left(\mathrm{4}^{{x}} −\mathrm{6}^{{x}} +\mathrm{9}^{{x}} \right)}{\left(\mathrm{2}^{{x}} +\mathrm{3}^{{x}} \right)\mathrm{6}^{{x}} }=\frac{\mathrm{7}}{\mathrm{6}} \\ $$$$\mathrm{6}×\mathrm{4}^{{x}} −\mathrm{13}×\mathrm{6}^{{x}} +\mathrm{6}×\mathrm{9}^{{x}} =\mathrm{0} \\ $$$$\mathrm{obviously}\:\mathrm{6}×\mathrm{4}−\mathrm{13}×\mathrm{6}+\mathrm{6}×\mathrm{9}=\mathrm{0} \\ $$$$\Rightarrow\:{x}=\mathrm{1} \\ $$$$\mathrm{less}\:\mathrm{obviously} \\ $$$$\frac{\mathrm{6}}{\mathrm{4}}−\frac{\mathrm{13}}{\mathrm{6}}+\frac{\mathrm{6}}{\mathrm{9}}=\mathrm{0} \\ $$$$\Rightarrow\:{x}=−\mathrm{1} \\ $$
Commented by Mastermind last updated on 07/Apr/22
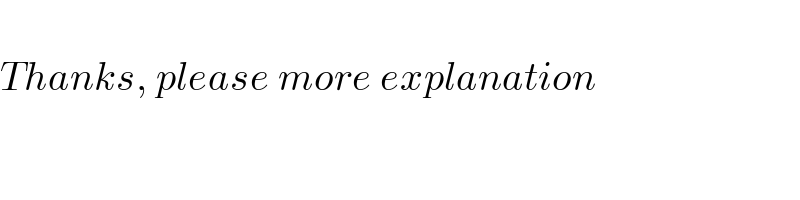
$$ \\ $$$${Thanks},\:{please}\:{more}\:{explanation} \\ $$
Commented by MJS_new last updated on 07/Apr/22
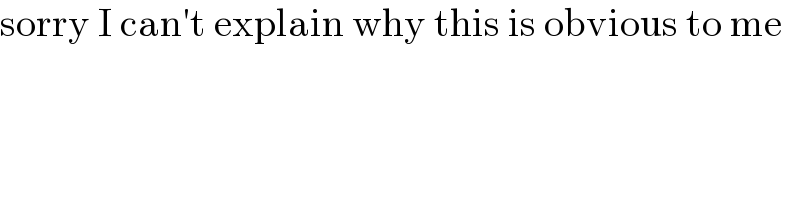
$$\mathrm{sorry}\:\mathrm{I}\:\mathrm{can}'\mathrm{t}\:\mathrm{explain}\:\mathrm{why}\:\mathrm{this}\:\mathrm{is}\:\mathrm{obvious}\:\mathrm{to}\:\mathrm{me} \\ $$
Commented by Mastermind last updated on 07/Apr/22
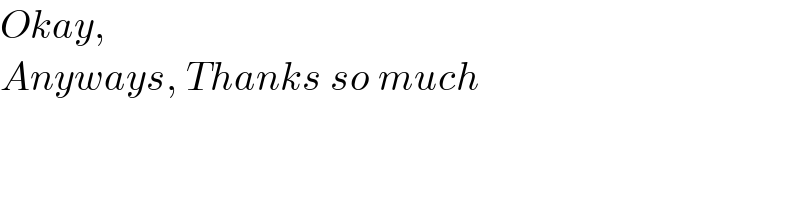
$${Okay}, \\ $$$${Anyways},\:{Thanks}\:{so}\:{much} \\ $$
Answered by cortano1 last updated on 07/Apr/22

$$\:\:\frac{\mathrm{8}^{{x}} +\mathrm{27}^{{x}} }{\mathrm{12}^{{x}} +\mathrm{18}^{{x}} }\:=\:\frac{\mathrm{7}}{\mathrm{6}} \\ $$$$\:\Rightarrow\frac{\left(\mathrm{2}^{{x}} \right)^{\mathrm{3}} +\left(\mathrm{3}^{{x}} \right)^{\mathrm{3}} }{\left(\mathrm{2}^{{x}} \right)^{\mathrm{2}} \left(\mathrm{3}^{{x}} \right)+\left(\mathrm{3}^{{x}} \right)^{\mathrm{2}} \left(\mathrm{2}^{{x}} \right)}\:=\:\frac{\mathrm{7}}{\mathrm{6}} \\ $$$$\Rightarrow\:\frac{\left(\frac{\mathrm{2}^{{x}} }{\mathrm{3}^{{x}} }\right)^{\mathrm{3}} +\mathrm{1}}{\left(\frac{\mathrm{2}^{{x}} }{\mathrm{3}^{{x}} }\right)^{\mathrm{2}} +\left(\frac{\mathrm{2}^{{x}} }{\mathrm{3}^{{x}} }\right)}\:=\:\frac{\mathrm{7}}{\mathrm{6}} \\ $$$$\:{let}\:\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{x}} \:=\:{d}\:;\:{d}>\mathrm{0} \\ $$$$\Rightarrow\:\frac{{d}^{\mathrm{3}} +\mathrm{1}}{{d}^{\mathrm{2}} +{d}}\:=\:\frac{\mathrm{7}}{\mathrm{6}} \\ $$$$\Rightarrow\frac{\left({d}+\mathrm{1}\right)\left({d}^{\mathrm{2}} −{d}+\mathrm{1}\right)}{{d}\left({d}+\mathrm{1}\right)}\:=\:\frac{\mathrm{7}}{\mathrm{6}} \\ $$$$\Rightarrow\mathrm{6}{d}^{\mathrm{2}} −\mathrm{6}{d}+\mathrm{6}=\:\mathrm{7}{d} \\ $$$$\Rightarrow\mathrm{6}{d}^{\mathrm{2}} −\mathrm{13}{d}+\mathrm{6}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{2}{d}−\mathrm{3}\right)\left(\mathrm{3}{d}−\mathrm{2}\right)=\mathrm{0} \\ $$$$\Rightarrow\begin{cases}{{d}=\frac{\mathrm{3}}{\mathrm{2}}\Rightarrow\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{x}} =\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{−\mathrm{1}} ;\:{x}=−\mathrm{1}}\\{{d}=\frac{\mathrm{2}}{\mathrm{3}}\Rightarrow\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{x}} =\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{1}} ;\:{x}=\mathrm{1}}\end{cases} \\ $$$$\:{check}\::\:{x}=\mathrm{1}\Rightarrow\frac{\mathrm{8}+\mathrm{27}}{\mathrm{12}+\mathrm{18}}=\frac{\mathrm{35}}{\mathrm{30}}=\frac{\mathrm{7}}{\mathrm{6}} \\ $$$$\:{x}=−\mathrm{1}\Rightarrow\frac{\frac{\mathrm{1}}{\mathrm{18}}+\frac{\mathrm{1}}{\mathrm{27}}}{\frac{\mathrm{1}}{\mathrm{12}}+\frac{\mathrm{1}}{\mathrm{18}}}\:=\:\frac{\mathrm{7}}{\mathrm{6}} \\ $$
Commented by peter frank last updated on 07/Apr/22

$$\mathrm{good} \\ $$
Commented by Mastermind last updated on 07/Apr/22
$$ \\ $$$${you}\:{did}\:{a}\:{great}\:{Job} \\ $$
