Menu Close

Solve-for-x-and-y-1-x-1-y-4-i-x-2-y-y-2-x-9-ii-

Tinku Tara 0 Comments
Pin




Question Number 58529 by Tawa1 last updated on 24/Apr/19
Solve for x and y (1/x) + (1/y) = 4 ....... (i) (x^2 /y) + (y^2 /x) = 9 ....... (ii)
$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{x}\:\mathrm{and}\:\mathrm{y} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{x}}\:+\:\frac{\mathrm{1}}{\mathrm{y}}\:=\:\mathrm{4}\:\:\:\:\:\:\:…….\:\left(\mathrm{i}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{y}}\:+\:\frac{\mathrm{y}^{\mathrm{2}} }{\mathrm{x}}\:\:=\:\:\mathrm{9}\:\:\:\:\:\:…….\:\left(\mathrm{ii}\right) \\ $$
Commented by MJS last updated on 24/Apr/19
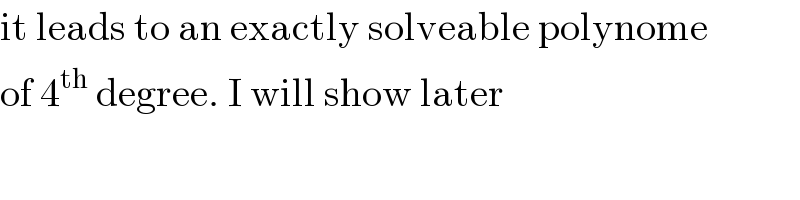
it leads to an exactly solveable polynome of 4^(th) degree. I will show later
$$\mathrm{it}\:\mathrm{leads}\:\mathrm{to}\:\mathrm{an}\:\mathrm{exactly}\:\mathrm{solveable}\:\mathrm{polynome} \\ $$$$\mathrm{of}\:\mathrm{4}^{\mathrm{th}} \:\mathrm{degree}.\:\mathrm{I}\:\mathrm{will}\:\mathrm{show}\:\mathrm{later} \\ $$
Commented by Tawa1 last updated on 24/Apr/19
Waiting sir. God bless you
$$\mathrm{Waiting}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you} \\ $$
Commented by behi83417@gmail.com last updated on 25/Apr/19
x+y=4xy x^3 +y^3 =9xy⇒[x+y=p,xy=q]⇒p^3 −3pq=9q ⇒ { ((p=4q)),((p^3 −3pq=9q⇒(4q)^3 −3(4q)q=9q)) :} ⇒64q^3 −12q^2 −9q=0⇒q(64q^2 −12q−9)=0 ⇒1)q=0⇒(x=0∨y=0,not ok for original question) ⇒2) 64q^2 −12q−9=0⇒q=((6±(√(36+9×64)))/(64)) ⇒[q=xy=3×((1±(√(17)))/(32))⇒p=x+y=3×((1±(√(17)))/8)] z^2 −(3/8)(1±(√(17)))z+(3/(32))(1±(√(17)))=0 z_(1,2) =(3/(16))[(1+(√(17)))±(√((1+(√(17)))^2 −(1+(√(17)))))] =(3/(16))[(1+(√(17)))±(√(17+(√(17))))] z_(3,4) =(3/(16))[(1−(√(17)))±(√((1−(√(17)))^2 −(1−(√(17)))))] =(3/(16))[(1−(√(17)))±(√(17−(√(17))))] z_(5,6) =(3/(16))[(1+(√(17)))±(√((1+(√(17)))^2 −(1−(√(17)))))] =(3/(16))[(1+(√(17)))±(√(17+3(√(17))))] z_(7,8) =(3/(16))[(1−(√(17)))±(√((1−(√(17)))^2 −(1+(√(17)))))] =(3/(16))[(1−(√(17)))±(√(17−3(√(17))))]
$${x}+{y}=\mathrm{4}{xy} \\ $$$${x}^{\mathrm{3}} +{y}^{\mathrm{3}} =\mathrm{9}{xy}\Rightarrow\left[{x}+{y}={p},{xy}={q}\right]\Rightarrow{p}^{\mathrm{3}} −\mathrm{3}{pq}=\mathrm{9}{q} \\ $$$$\Rightarrow\begin{cases}{{p}=\mathrm{4}{q}}\\{{p}^{\mathrm{3}} −\mathrm{3}{pq}=\mathrm{9}{q}\Rightarrow\left(\mathrm{4}{q}\right)^{\mathrm{3}} −\mathrm{3}\left(\mathrm{4}{q}\right){q}=\mathrm{9}{q}}\end{cases} \\ $$$$\Rightarrow\mathrm{64}{q}^{\mathrm{3}} −\mathrm{12}{q}^{\mathrm{2}} −\mathrm{9}{q}=\mathrm{0}\Rightarrow{q}\left(\mathrm{64}{q}^{\mathrm{2}} −\mathrm{12}{q}−\mathrm{9}\right)=\mathrm{0} \\ $$$$\left.\Rightarrow\mathrm{1}\right){q}=\mathrm{0}\Rightarrow\left({x}=\mathrm{0}\vee{y}=\mathrm{0},{not}\:{ok}\:{for}\:{original}\right. \\ $$$$\left.{question}\right) \\ $$$$\left.\Rightarrow\mathrm{2}\right)\:\mathrm{64}{q}^{\mathrm{2}} −\mathrm{12}{q}−\mathrm{9}=\mathrm{0}\Rightarrow{q}=\frac{\mathrm{6}\pm\sqrt{\mathrm{36}+\mathrm{9}×\mathrm{64}}}{\mathrm{64}} \\ $$$$\Rightarrow\left[{q}=\boldsymbol{\mathrm{xy}}=\mathrm{3}×\frac{\mathrm{1}\pm\sqrt{\mathrm{17}}}{\mathrm{32}}\Rightarrow{p}=\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}=\mathrm{3}×\frac{\mathrm{1}\pm\sqrt{\mathrm{17}}}{\mathrm{8}}\right] \\ $$$$\boldsymbol{\mathrm{z}}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{8}}\left(\mathrm{1}\pm\sqrt{\mathrm{17}}\right)\boldsymbol{\mathrm{z}}+\frac{\mathrm{3}}{\mathrm{32}}\left(\mathrm{1}\pm\sqrt{\mathrm{17}}\right)=\mathrm{0} \\ $$$$\boldsymbol{\mathrm{z}}_{\mathrm{1},\mathrm{2}} =\frac{\mathrm{3}}{\mathrm{16}}\left[\left(\mathrm{1}+\sqrt{\mathrm{17}}\right)\pm\sqrt{\left(\mathrm{1}+\sqrt{\mathrm{17}}\right)^{\mathrm{2}} −\left(\mathrm{1}+\sqrt{\mathrm{17}}\right)}\right] \\ $$$$=\frac{\mathrm{3}}{\mathrm{16}}\left[\left(\mathrm{1}+\sqrt{\mathrm{17}}\right)\pm\sqrt{\mathrm{17}+\sqrt{\mathrm{17}}}\right] \\ $$$$\boldsymbol{\mathrm{z}}_{\mathrm{3},\mathrm{4}} =\frac{\mathrm{3}}{\mathrm{16}}\left[\left(\mathrm{1}−\sqrt{\mathrm{17}}\right)\pm\sqrt{\left(\mathrm{1}−\sqrt{\mathrm{17}}\right)^{\mathrm{2}} −\left(\mathrm{1}−\sqrt{\mathrm{17}}\right)}\right] \\ $$$$=\frac{\mathrm{3}}{\mathrm{16}}\left[\left(\mathrm{1}−\sqrt{\mathrm{17}}\right)\pm\sqrt{\mathrm{17}−\sqrt{\mathrm{17}}}\right] \\ $$$$\boldsymbol{\mathrm{z}}_{\mathrm{5},\mathrm{6}} =\frac{\mathrm{3}}{\mathrm{16}}\left[\left(\mathrm{1}+\sqrt{\mathrm{17}}\right)\pm\sqrt{\left(\mathrm{1}+\sqrt{\mathrm{17}}\right)^{\mathrm{2}} −\left(\mathrm{1}−\sqrt{\mathrm{17}}\right)}\right] \\ $$$$=\frac{\mathrm{3}}{\mathrm{16}}\left[\left(\mathrm{1}+\sqrt{\mathrm{17}}\right)\pm\sqrt{\mathrm{17}+\mathrm{3}\sqrt{\mathrm{17}}}\right] \\ $$$$\boldsymbol{\mathrm{z}}_{\mathrm{7},\mathrm{8}} =\frac{\mathrm{3}}{\mathrm{16}}\left[\left(\mathrm{1}−\sqrt{\mathrm{17}}\right)\pm\sqrt{\left(\mathrm{1}−\sqrt{\mathrm{17}}\right)^{\mathrm{2}} −\left(\mathrm{1}+\sqrt{\mathrm{17}}\right)}\right] \\ $$$$=\frac{\mathrm{3}}{\mathrm{16}}\left[\left(\mathrm{1}−\sqrt{\mathrm{17}}\right)\pm\sqrt{\mathrm{17}−\mathrm{3}\sqrt{\mathrm{17}}}\right] \\ $$
Commented by Tawa1 last updated on 25/Apr/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by MJS last updated on 25/Apr/19
(i) ⇒ y=(x/(4x−1)) ⇒ ⇒ (ii) x^4 −(3/4)x^3 −((33)/(16))x^2 +(9/8)x−(9/(64))=0 put x_(1, 2) =α±(√β); x_(3, 4) =γ±(√δ) (x−x_1 )(x−x_2 )(x−x_3 )(x−x_4 )=0 x^4 −2(α+γ)x^3 +(α^2 +4αγ−β+γ^2 +δ)x^2 −2(αγ(α+γ)+αδ−βγ)x+(α^2 −β)(γ^2 +δ)=0 now compare factors: (1) −2(α+γ)=−(3/4) (2) α^2 +4αγ−β+γ^2 +δ=−((33)/(16)) (3) −2(αγ(α+γ)+αδ−βγ)=(9/8) (4) (α^2 −β)(γ^2 +δ)=−(9/(64)) now solve (1) for α, (2) for β, (3) for γ α=(3/8)−γ β=−2γ^2 +(3/4)γ+δ+((141)/(64)) δ=((32γ^3 −18γ^2 −33γ+9)/(2(16γ−3))) ⇒ (4) γ^6 −(9/8)γ^5 −((39)/(64))γ^4 +((369)/(512))γ^3 +((423)/(4096))γ^2 −((3051)/(32768))γ+((567)/(65536))=0 γ=r+(3/(16)) r^6 −((291)/(256))r^4 +((21267)/(65536))r^2 −((23409)/(16777216))=0 r=(√s) s^3 −((291)/(256))s^2 +((21267)/(65536))s−((23409)/(16777216))=0 s=t+((97)/(256)) t^3 −((435)/(4096))t+((1673)/(131072))=0 trying factors of ((1673)/(131072)) ⇒ t_1 =(7/(32)) (we don′t need t_(2, 3) =−(7/(64))±((12(√2))/(64))) t=(7/(32)) ⇒ s=((153)/(256)) ⇒ r=((3(√(17)))/(16)) ⇒ γ=(3/(16))+((3(√(17)))/(16)) now α=(3/(16))−((3(√(17)))/(16)) β=((69)/(128))+((3(√(17)))/(128)) γ=(3/(16))+((3(√(17)))/(16)) δ=−((69)/(128))+((3(√(17)))/(16)) ⇒ x_1 =(3/(16))−((3(√(17)))/(16))−((√(6(23+(√(17)))))/(16)) x_2 =(3/(16))−((3(√(17)))/(16))+((√(6(23+(√(17)))))/(16)) x_(3, 4) ∉R y_1 =x_2 y_2 =x_1
$$\left(\mathrm{i}\right)\:\Rightarrow\:{y}=\frac{{x}}{\mathrm{4}{x}−\mathrm{1}}\:\Rightarrow \\ $$$$\Rightarrow\:\left(\mathrm{ii}\right)\:{x}^{\mathrm{4}} −\frac{\mathrm{3}}{\mathrm{4}}{x}^{\mathrm{3}} −\frac{\mathrm{33}}{\mathrm{16}}{x}^{\mathrm{2}} +\frac{\mathrm{9}}{\mathrm{8}}{x}−\frac{\mathrm{9}}{\mathrm{64}}=\mathrm{0} \\ $$$$\mathrm{put}\:{x}_{\mathrm{1},\:\mathrm{2}} =\alpha\pm\sqrt{\beta};\:{x}_{\mathrm{3},\:\mathrm{4}} =\gamma\pm\sqrt{\delta} \\ $$$$\left({x}−{x}_{\mathrm{1}} \right)\left({x}−{x}_{\mathrm{2}} \right)\left({x}−{x}_{\mathrm{3}} \right)\left({x}−{x}_{\mathrm{4}} \right)=\mathrm{0} \\ $$$${x}^{\mathrm{4}} −\mathrm{2}\left(\alpha+\gamma\right){x}^{\mathrm{3}} +\left(\alpha^{\mathrm{2}} +\mathrm{4}\alpha\gamma−\beta+\gamma^{\mathrm{2}} +\delta\right){x}^{\mathrm{2}} −\mathrm{2}\left(\alpha\gamma\left(\alpha+\gamma\right)+\alpha\delta−\beta\gamma\right){x}+\left(\alpha^{\mathrm{2}} −\beta\right)\left(\gamma^{\mathrm{2}} +\delta\right)=\mathrm{0} \\ $$$$\mathrm{now}\:\mathrm{compare}\:\mathrm{factors}: \\ $$$$\left(\mathrm{1}\right)\:\:−\mathrm{2}\left(\alpha+\gamma\right)=−\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\left(\mathrm{2}\right)\:\:\alpha^{\mathrm{2}} +\mathrm{4}\alpha\gamma−\beta+\gamma^{\mathrm{2}} +\delta=−\frac{\mathrm{33}}{\mathrm{16}} \\ $$$$\left(\mathrm{3}\right)\:\:−\mathrm{2}\left(\alpha\gamma\left(\alpha+\gamma\right)+\alpha\delta−\beta\gamma\right)=\frac{\mathrm{9}}{\mathrm{8}} \\ $$$$\left(\mathrm{4}\right)\:\:\left(\alpha^{\mathrm{2}} −\beta\right)\left(\gamma^{\mathrm{2}} +\delta\right)=−\frac{\mathrm{9}}{\mathrm{64}} \\ $$$$\mathrm{now}\:\mathrm{solve}\:\left(\mathrm{1}\right)\:\mathrm{for}\:\alpha,\:\left(\mathrm{2}\right)\:\mathrm{for}\:\beta,\:\left(\mathrm{3}\right)\:\mathrm{for}\:\gamma \\ $$$$\alpha=\frac{\mathrm{3}}{\mathrm{8}}−\gamma \\ $$$$\beta=−\mathrm{2}\gamma^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}\gamma+\delta+\frac{\mathrm{141}}{\mathrm{64}} \\ $$$$\delta=\frac{\mathrm{32}\gamma^{\mathrm{3}} −\mathrm{18}\gamma^{\mathrm{2}} −\mathrm{33}\gamma+\mathrm{9}}{\mathrm{2}\left(\mathrm{16}\gamma−\mathrm{3}\right)} \\ $$$$\Rightarrow\:\left(\mathrm{4}\right) \\ $$$$\gamma^{\mathrm{6}} −\frac{\mathrm{9}}{\mathrm{8}}\gamma^{\mathrm{5}} −\frac{\mathrm{39}}{\mathrm{64}}\gamma^{\mathrm{4}} +\frac{\mathrm{369}}{\mathrm{512}}\gamma^{\mathrm{3}} +\frac{\mathrm{423}}{\mathrm{4096}}\gamma^{\mathrm{2}} −\frac{\mathrm{3051}}{\mathrm{32768}}\gamma+\frac{\mathrm{567}}{\mathrm{65536}}=\mathrm{0} \\ $$$$\gamma={r}+\frac{\mathrm{3}}{\mathrm{16}} \\ $$$${r}^{\mathrm{6}} −\frac{\mathrm{291}}{\mathrm{256}}{r}^{\mathrm{4}} +\frac{\mathrm{21267}}{\mathrm{65536}}{r}^{\mathrm{2}} −\frac{\mathrm{23409}}{\mathrm{16777216}}=\mathrm{0} \\ $$$${r}=\sqrt{{s}} \\ $$$${s}^{\mathrm{3}} −\frac{\mathrm{291}}{\mathrm{256}}{s}^{\mathrm{2}} +\frac{\mathrm{21267}}{\mathrm{65536}}{s}−\frac{\mathrm{23409}}{\mathrm{16777216}}=\mathrm{0} \\ $$$${s}={t}+\frac{\mathrm{97}}{\mathrm{256}} \\ $$$${t}^{\mathrm{3}} −\frac{\mathrm{435}}{\mathrm{4096}}{t}+\frac{\mathrm{1673}}{\mathrm{131072}}=\mathrm{0} \\ $$$$\mathrm{trying}\:\mathrm{factors}\:\mathrm{of}\:\frac{\mathrm{1673}}{\mathrm{131072}}\:\Rightarrow\:{t}_{\mathrm{1}} =\frac{\mathrm{7}}{\mathrm{32}} \\ $$$$\left(\mathrm{we}\:\mathrm{don}'\mathrm{t}\:\mathrm{need}\:{t}_{\mathrm{2},\:\mathrm{3}} =−\frac{\mathrm{7}}{\mathrm{64}}\pm\frac{\mathrm{12}\sqrt{\mathrm{2}}}{\mathrm{64}}\right) \\ $$$${t}=\frac{\mathrm{7}}{\mathrm{32}}\:\Rightarrow\:{s}=\frac{\mathrm{153}}{\mathrm{256}}\:\Rightarrow\:{r}=\frac{\mathrm{3}\sqrt{\mathrm{17}}}{\mathrm{16}}\:\Rightarrow\:\gamma=\frac{\mathrm{3}}{\mathrm{16}}+\frac{\mathrm{3}\sqrt{\mathrm{17}}}{\mathrm{16}} \\ $$$$\mathrm{now} \\ $$$$\alpha=\frac{\mathrm{3}}{\mathrm{16}}−\frac{\mathrm{3}\sqrt{\mathrm{17}}}{\mathrm{16}} \\ $$$$\beta=\frac{\mathrm{69}}{\mathrm{128}}+\frac{\mathrm{3}\sqrt{\mathrm{17}}}{\mathrm{128}} \\ $$$$\gamma=\frac{\mathrm{3}}{\mathrm{16}}+\frac{\mathrm{3}\sqrt{\mathrm{17}}}{\mathrm{16}} \\ $$$$\delta=−\frac{\mathrm{69}}{\mathrm{128}}+\frac{\mathrm{3}\sqrt{\mathrm{17}}}{\mathrm{16}} \\ $$$$\Rightarrow \\ $$$${x}_{\mathrm{1}} =\frac{\mathrm{3}}{\mathrm{16}}−\frac{\mathrm{3}\sqrt{\mathrm{17}}}{\mathrm{16}}−\frac{\sqrt{\mathrm{6}\left(\mathrm{23}+\sqrt{\mathrm{17}}\right)}}{\mathrm{16}} \\ $$$${x}_{\mathrm{2}} =\frac{\mathrm{3}}{\mathrm{16}}−\frac{\mathrm{3}\sqrt{\mathrm{17}}}{\mathrm{16}}+\frac{\sqrt{\mathrm{6}\left(\mathrm{23}+\sqrt{\mathrm{17}}\right)}}{\mathrm{16}} \\ $$$${x}_{\mathrm{3},\:\mathrm{4}} \notin\mathbb{R} \\ $$$${y}_{\mathrm{1}} ={x}_{\mathrm{2}} \\ $$$${y}_{\mathrm{2}} ={x}_{\mathrm{1}} \\ $$
Commented by MJS last updated on 25/Apr/19
I prepared these formulas, the rest is just putting in the constants x^4 +ax^3 +bx^2 +cx+d=0 (x−α−(√β))(x−α+(√β))(x−γ−(√δ))(x−γ+(√δ))=0 (1) −2(α+γ)=a (2) α^2 +4αγ−β+γ^2 −δ=b (3) −2(αγ(α+γ)−αδ−βγ)=c (4) (α^2 −β)(γ^2 −δ)=d ⇒ (1) α=−γ−(a/2) (2) β=−2γ^2 −aγ−δ+(a^2 /4)−b (3) δ=−γ^2 −(a/2)γ+(((a^2 −4b)γ−2c)/(2(4γ+a))) ⇒ β=−γ^2 −(a/2)γ+((2(a^2 −4b)γ+a^3 −4ab+4c)/(4(4γ+a))) (4) γ^6 +((3a)/2)γ^5 +((3a^2 +2b)/4)γ^4 +((a(a^2 +4b))/8)γ^3 +((2a^2 b+ac+b^2 −4d)/(16))γ^2 +((a(ac+b^2 −4d))/(32))γ−((a^2 d−abc+c^2 )/(64))=0 γ=r−(a/4) r^6 −((3a^2 −8b)/(16))r^4 +((3a^4 −16(a^2 b−ac−b^2 +4d))/(256))r^2 −(((a^3 −4ab+8c)^2 )/(4096))=0 r=(√s) s^3 −((3a^2 −8b)/(16))s^2 +((3a^4 −16(a^2 b−ac−b^2 +4d))/(256))s−(((a^3 −4ab+8c)^2 )/(4096))=0 s=t+((3a^2 −8b)/(48)) t^3 +((3ac−b^2 −12d)/(48))t−((2b^3 +9(3a^2 d−abc−8bd+3c^2 ))/(1728))=0 p=((3ac−b^2 −12d)/(48)) q=−((2b^3 +9(3a^2 d−abc−8bd+3c^2 ))/(1728)) now we have to 1. try factors of q ⇒ solved 2. calculate D=(p^3 /(27))+(q^2 /4) and decide which method to use D<0 ⇒ trigonometric solution D≥0 ⇒ Cardano′s solution in most cases we won′t get useable solutions but we always get exact solutions γ=(√(t+((3a^2 −8b)/(48))))−(a/4) if t isn′t a “nice” number we cannot handle α, β, γ, δ nor x= { ((α±(√β))),((γ±(√δ))) :}
$$\mathrm{I}\:\mathrm{prepared}\:\mathrm{these}\:\mathrm{formulas},\:\mathrm{the}\:\mathrm{rest}\:\mathrm{is}\:\mathrm{just} \\ $$$$\mathrm{putting}\:\mathrm{in}\:\mathrm{the}\:\mathrm{constants} \\ $$$${x}^{\mathrm{4}} +{ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d}=\mathrm{0} \\ $$$$\left({x}−\alpha−\sqrt{\beta}\right)\left({x}−\alpha+\sqrt{\beta}\right)\left({x}−\gamma−\sqrt{\delta}\right)\left({x}−\gamma+\sqrt{\delta}\right)=\mathrm{0} \\ $$$$\left(\mathrm{1}\right)\:\:−\mathrm{2}\left(\alpha+\gamma\right)={a} \\ $$$$\left(\mathrm{2}\right)\:\:\alpha^{\mathrm{2}} +\mathrm{4}\alpha\gamma−\beta+\gamma^{\mathrm{2}} −\delta={b} \\ $$$$\left(\mathrm{3}\right)\:\:−\mathrm{2}\left(\alpha\gamma\left(\alpha+\gamma\right)−\alpha\delta−\beta\gamma\right)={c} \\ $$$$\left(\mathrm{4}\right)\:\:\left(\alpha^{\mathrm{2}} −\beta\right)\left(\gamma^{\mathrm{2}} −\delta\right)={d} \\ $$$$\Rightarrow \\ $$$$\left(\mathrm{1}\right)\:\:\alpha=−\gamma−\frac{{a}}{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\:\:\beta=−\mathrm{2}\gamma^{\mathrm{2}} −{a}\gamma−\delta+\frac{{a}^{\mathrm{2}} }{\mathrm{4}}−{b} \\ $$$$\left(\mathrm{3}\right)\:\:\delta=−\gamma^{\mathrm{2}} −\frac{{a}}{\mathrm{2}}\gamma+\frac{\left({a}^{\mathrm{2}} −\mathrm{4}{b}\right)\gamma−\mathrm{2}{c}}{\mathrm{2}\left(\mathrm{4}\gamma+{a}\right)} \\ $$$$\Rightarrow\:\beta=−\gamma^{\mathrm{2}} −\frac{{a}}{\mathrm{2}}\gamma+\frac{\mathrm{2}\left({a}^{\mathrm{2}} −\mathrm{4}{b}\right)\gamma+{a}^{\mathrm{3}} −\mathrm{4}{ab}+\mathrm{4}{c}}{\mathrm{4}\left(\mathrm{4}\gamma+{a}\right)} \\ $$$$\left(\mathrm{4}\right) \\ $$$$\gamma^{\mathrm{6}} +\frac{\mathrm{3}{a}}{\mathrm{2}}\gamma^{\mathrm{5}} +\frac{\mathrm{3}{a}^{\mathrm{2}} +\mathrm{2}{b}}{\mathrm{4}}\gamma^{\mathrm{4}} +\frac{{a}\left({a}^{\mathrm{2}} +\mathrm{4}{b}\right)}{\mathrm{8}}\gamma^{\mathrm{3}} +\frac{\mathrm{2}{a}^{\mathrm{2}} {b}+{ac}+{b}^{\mathrm{2}} −\mathrm{4}{d}}{\mathrm{16}}\gamma^{\mathrm{2}} +\frac{{a}\left({ac}+{b}^{\mathrm{2}} −\mathrm{4}{d}\right)}{\mathrm{32}}\gamma−\frac{{a}^{\mathrm{2}} {d}−{abc}+{c}^{\mathrm{2}} }{\mathrm{64}}=\mathrm{0} \\ $$$$\gamma={r}−\frac{{a}}{\mathrm{4}} \\ $$$${r}^{\mathrm{6}} −\frac{\mathrm{3}{a}^{\mathrm{2}} −\mathrm{8}{b}}{\mathrm{16}}{r}^{\mathrm{4}} +\frac{\mathrm{3}{a}^{\mathrm{4}} −\mathrm{16}\left({a}^{\mathrm{2}} {b}−{ac}−{b}^{\mathrm{2}} +\mathrm{4}{d}\right)}{\mathrm{256}}{r}^{\mathrm{2}} −\frac{\left({a}^{\mathrm{3}} −\mathrm{4}{ab}+\mathrm{8}{c}\right)^{\mathrm{2}} }{\mathrm{4096}}=\mathrm{0} \\ $$$${r}=\sqrt{{s}} \\ $$$${s}^{\mathrm{3}} −\frac{\mathrm{3}{a}^{\mathrm{2}} −\mathrm{8}{b}}{\mathrm{16}}{s}^{\mathrm{2}} +\frac{\mathrm{3}{a}^{\mathrm{4}} −\mathrm{16}\left({a}^{\mathrm{2}} {b}−{ac}−{b}^{\mathrm{2}} +\mathrm{4}{d}\right)}{\mathrm{256}}{s}−\frac{\left({a}^{\mathrm{3}} −\mathrm{4}{ab}+\mathrm{8}{c}\right)^{\mathrm{2}} }{\mathrm{4096}}=\mathrm{0} \\ $$$${s}={t}+\frac{\mathrm{3}{a}^{\mathrm{2}} −\mathrm{8}{b}}{\mathrm{48}} \\ $$$${t}^{\mathrm{3}} +\frac{\mathrm{3}{ac}−{b}^{\mathrm{2}} −\mathrm{12}{d}}{\mathrm{48}}{t}−\frac{\mathrm{2}{b}^{\mathrm{3}} +\mathrm{9}\left(\mathrm{3}{a}^{\mathrm{2}} {d}−{abc}−\mathrm{8}{bd}+\mathrm{3}{c}^{\mathrm{2}} \right)}{\mathrm{1728}}=\mathrm{0} \\ $$$${p}=\frac{\mathrm{3}{ac}−{b}^{\mathrm{2}} −\mathrm{12}{d}}{\mathrm{48}} \\ $$$${q}=−\frac{\mathrm{2}{b}^{\mathrm{3}} +\mathrm{9}\left(\mathrm{3}{a}^{\mathrm{2}} {d}−{abc}−\mathrm{8}{bd}+\mathrm{3}{c}^{\mathrm{2}} \right)}{\mathrm{1728}} \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{have}\:\mathrm{to} \\ $$$$\mathrm{1}.\:\mathrm{try}\:\mathrm{factors}\:\mathrm{of}\:{q}\:\Rightarrow\:\mathrm{solved} \\ $$$$\mathrm{2}.\:\mathrm{calculate} \\ $$$${D}=\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}}\:\mathrm{and}\:\mathrm{decide}\:\mathrm{which}\:\mathrm{method}\:\mathrm{to}\:\mathrm{use} \\ $$$${D}<\mathrm{0}\:\Rightarrow\:\mathrm{trigonometric}\:\mathrm{solution} \\ $$$${D}\geqslant\mathrm{0}\:\Rightarrow\:\mathrm{Cardano}'\mathrm{s}\:\mathrm{solution} \\ $$$$\mathrm{in}\:\mathrm{most}\:\mathrm{cases}\:\mathrm{we}\:\mathrm{won}'\mathrm{t}\:\mathrm{get}\:\mathrm{useable}\:\mathrm{solutions} \\ $$$$\mathrm{but}\:\mathrm{we}\:\mathrm{always}\:\mathrm{get}\:\mathrm{exact}\:\mathrm{solutions} \\ $$$$\gamma=\sqrt{{t}+\frac{\mathrm{3}{a}^{\mathrm{2}} −\mathrm{8}{b}}{\mathrm{48}}}−\frac{{a}}{\mathrm{4}} \\ $$$$\mathrm{if}\:{t}\:\mathrm{isn}'\mathrm{t}\:\mathrm{a}\:“\mathrm{nice}''\:\mathrm{number}\:\mathrm{we}\:\mathrm{cannot}\:\mathrm{handle} \\ $$$$\alpha,\:\beta,\:\gamma,\:\delta\:\mathrm{nor}\:{x}=\begin{cases}{\alpha\pm\sqrt{\beta}}\\{\gamma\pm\sqrt{\delta}}\end{cases} \\ $$
Commented by Tawa1 last updated on 24/Apr/19
God bless you sir, i appreciate your time sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir} \\ $$
Commented by tanmay last updated on 25/Apr/19
without using calculator how to solve this problem? is it feasible to caculate such big number 65536,16777216,33768 etc to calculate by simple +,−,×,/ etc
$${without}\:{using}\:{calculator}\:{how}\:{to}\:{solve}\:{this}\:{problem}? \\ $$$${is}\:{it}\:{feasible}\:{to}\:{caculate}\:{such}\:{big}\:{number} \\ $$$$\mathrm{65536},\mathrm{16777216},\mathrm{33768}\:{etc}\:{to}\:{calculate}\:{by}\:{simple} \\ $$$$+,−,×,/\:{etc} \\ $$$$ \\ $$
Commented by tanmay last updated on 25/Apr/19
ok sir
$${ok}\:{sir} \\ $$
Answered by tanmay last updated on 24/Apr/19
x+y=4xy x^3 +y^3 =9xy (x+y)^3 −3xy(x+y)=9xy 64x^3 y^3 −12x^2 y^2 −9xy=0 xy≠0 64x^2 y^2 −12xy−9=0 xy=((12±(√(144+64×36)))/(2×64))=a x+y=4a xy=a x(4a−x)=a −x^2 +4ax−a=0 x^2 −4ax+a=0 x=((4a±(√(16a^2 −4a)))/2) y=4a−(((4a±(√(16a^2 −4a)))/2)) pls calculate value of a ...i have apathy to caculate
$${x}+{y}=\mathrm{4}{xy} \\ $$$${x}^{\mathrm{3}} +{y}^{\mathrm{3}} =\mathrm{9}{xy} \\ $$$$\left({x}+{y}\right)^{\mathrm{3}} −\mathrm{3}{xy}\left({x}+{y}\right)=\mathrm{9}{xy} \\ $$$$\mathrm{64}{x}^{\mathrm{3}} {y}^{\mathrm{3}} −\mathrm{12}{x}^{\mathrm{2}} {y}^{\mathrm{2}} −\mathrm{9}{xy}=\mathrm{0} \\ $$$${xy}\neq\mathrm{0} \\ $$$$\mathrm{64}{x}^{\mathrm{2}} {y}^{\mathrm{2}} −\mathrm{12}{xy}−\mathrm{9}=\mathrm{0} \\ $$$${xy}=\frac{\mathrm{12}\pm\sqrt{\mathrm{144}+\mathrm{64}×\mathrm{36}}}{\mathrm{2}×\mathrm{64}}={a} \\ $$$$ \\ $$$${x}+{y}=\mathrm{4}{a} \\ $$$${xy}={a} \\ $$$${x}\left(\mathrm{4}{a}−{x}\right)={a} \\ $$$$−{x}^{\mathrm{2}} +\mathrm{4}{ax}−{a}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\mathrm{4}{ax}+{a}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{4}{a}\pm\sqrt{\mathrm{16}{a}^{\mathrm{2}} −\mathrm{4}{a}}}{\mathrm{2}} \\ $$$${y}=\mathrm{4}{a}−\left(\frac{\mathrm{4}{a}\pm\sqrt{\mathrm{16}{a}^{\mathrm{2}} −\mathrm{4}{a}}}{\mathrm{2}}\right) \\ $$$${pls}\:{calculate}\:{value}\:{of}\:{a}\:…{i}\:{have}\:{apathy}\:{to}\:{caculate} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Tawa1 last updated on 24/Apr/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by Rasheed.Sindhi last updated on 24/Apr/19
(i)⇒((x+y)/(xy))=4 .......(iii) (ii)⇒((x^3 +y^3 )/(xy))=9 ......(iv) (iv)÷(iii):((x^3 +y^3 )/(x+y))=(9/4) x^2 +y^2 −xy=(9/4) (x+y)^2 −3xy=(9/4) From (iii) xy=((x+y)/4) So (x+y)^2 −3(((x+y)/4))−(9/4)=0 4(x+y)^2 −3(x+y)−9=0 x+y=((3±(√(9−4(4)(−9))))/(2(4))) =((3±3(√(17)))/8) Continue
$$\left(\mathrm{i}\right)\Rightarrow\frac{\mathrm{x}+\mathrm{y}}{\mathrm{xy}}=\mathrm{4}\:…….\left(\mathrm{iii}\right) \\ $$$$\left(\mathrm{ii}\right)\Rightarrow\frac{\mathrm{x}^{\mathrm{3}} +\mathrm{y}^{\mathrm{3}} }{\mathrm{xy}}=\mathrm{9}\:……\left(\mathrm{iv}\right) \\ $$$$\left(\mathrm{iv}\right)\boldsymbol{\div}\left(\mathrm{iii}\right):\frac{\mathrm{x}^{\mathrm{3}} +\mathrm{y}^{\mathrm{3}} }{\mathrm{x}+\mathrm{y}}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{xy}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} −\mathrm{3xy}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\mathrm{From}\:\left(\mathrm{iii}\right)\:\mathrm{xy}=\frac{\mathrm{x}+\mathrm{y}}{\mathrm{4}} \\ $$$$\mathrm{So}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} −\mathrm{3}\left(\frac{\mathrm{x}+\mathrm{y}}{\mathrm{4}}\right)−\frac{\mathrm{9}}{\mathrm{4}}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{4}\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} −\mathrm{3}\left(\mathrm{x}+\mathrm{y}\right)−\mathrm{9}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}+\mathrm{y}=\frac{\mathrm{3}\pm\sqrt{\mathrm{9}−\mathrm{4}\left(\mathrm{4}\right)\left(−\mathrm{9}\right)}}{\mathrm{2}\left(\mathrm{4}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{3}\pm\mathrm{3}\sqrt{\mathrm{17}}}{\mathrm{8}} \\ $$$${Continue} \\ $$
Commented by Tawa1 last updated on 24/Apr/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *