Question Number 79423 by Rio Michael last updated on 25/Jan/20
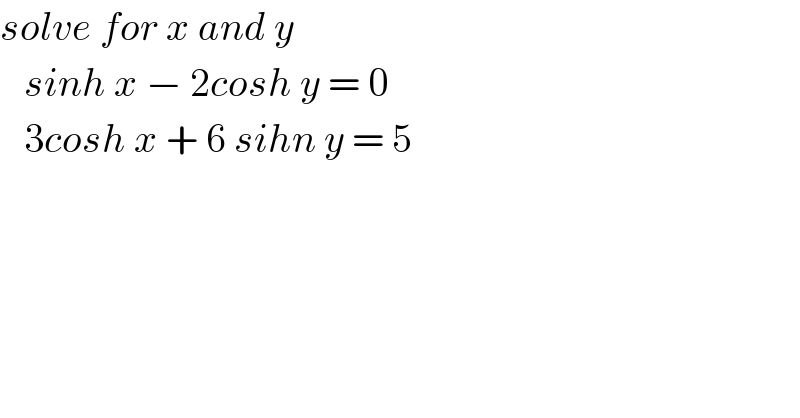
$${solve}\:{for}\:{x}\:{and}\:{y}\: \\ $$$$\:\:\:{sinh}\:{x}\:−\:\mathrm{2}{cosh}\:{y}\:=\:\mathrm{0} \\ $$$$\:\:\:\mathrm{3}{cosh}\:{x}\:+\:\mathrm{6}\:{sihn}\:{y}\:=\:\mathrm{5} \\ $$
Answered by mr W last updated on 25/Jan/20
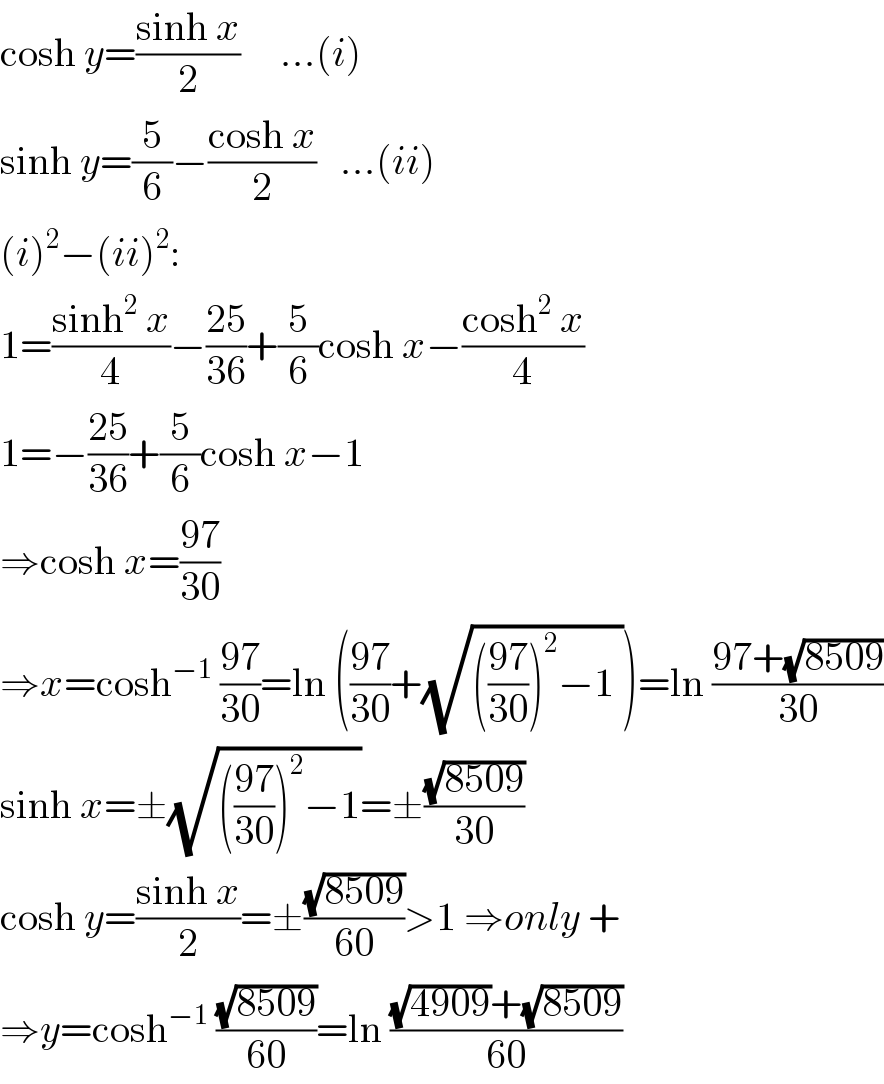
$$\mathrm{cosh}\:{y}=\frac{\mathrm{sinh}\:{x}}{\mathrm{2}}\:\:\:\:\:…\left({i}\right) \\ $$$$\mathrm{sinh}\:{y}=\frac{\mathrm{5}}{\mathrm{6}}−\frac{\mathrm{cosh}\:{x}}{\mathrm{2}}\:\:\:…\left({ii}\right) \\ $$$$\left({i}\right)^{\mathrm{2}} −\left({ii}\right)^{\mathrm{2}} : \\ $$$$\mathrm{1}=\frac{\mathrm{sinh}^{\mathrm{2}} \:{x}}{\mathrm{4}}−\frac{\mathrm{25}}{\mathrm{36}}+\frac{\mathrm{5}}{\mathrm{6}}\mathrm{cosh}\:{x}−\frac{\mathrm{cosh}^{\mathrm{2}} \:{x}}{\mathrm{4}} \\ $$$$\mathrm{1}=−\frac{\mathrm{25}}{\mathrm{36}}+\frac{\mathrm{5}}{\mathrm{6}}\mathrm{cosh}\:{x}−\mathrm{1} \\ $$$$\Rightarrow\mathrm{cosh}\:{x}=\frac{\mathrm{97}}{\mathrm{30}} \\ $$$$\Rightarrow{x}=\mathrm{cosh}^{−\mathrm{1}} \:\frac{\mathrm{97}}{\mathrm{30}}=\mathrm{ln}\:\left(\frac{\mathrm{97}}{\mathrm{30}}+\sqrt{\left(\frac{\mathrm{97}}{\mathrm{30}}\right)^{\mathrm{2}} −\mathrm{1}\:}\right)=\mathrm{ln}\:\frac{\mathrm{97}+\sqrt{\mathrm{8509}}}{\mathrm{30}} \\ $$$$\mathrm{sinh}\:{x}=\pm\sqrt{\left(\frac{\mathrm{97}}{\mathrm{30}}\right)^{\mathrm{2}} −\mathrm{1}}=\pm\frac{\sqrt{\mathrm{8509}}}{\mathrm{30}} \\ $$$$\mathrm{cosh}\:{y}=\frac{\mathrm{sinh}\:{x}}{\mathrm{2}}=\pm\frac{\sqrt{\mathrm{8509}}}{\mathrm{60}}>\mathrm{1}\:\Rightarrow{only}\:+ \\ $$$$\Rightarrow{y}=\mathrm{cosh}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{8509}}}{\mathrm{60}}=\mathrm{ln}\:\frac{\sqrt{\mathrm{4909}}+\sqrt{\mathrm{8509}}}{\mathrm{60}} \\ $$
Commented by Rio Michael last updated on 27/Jan/20

$${thanks}\:{sir},{seems}\:{like}\:{hyperbolic}\:{functions}\:{don}'{t} \\ $$$${suit}\:{simultaneous}\:{equations} \\ $$
