Question Number 90739 by ajfour last updated on 25/Apr/20
![solve for x and y tan^2 [π(x+y)]+cot^2 [π(x+y)] =1+(√((2x)/(x^2 +1)))](https://www.tinkutara.com/question/Q90739.png)
Commented by me2love2math last updated on 26/Apr/20
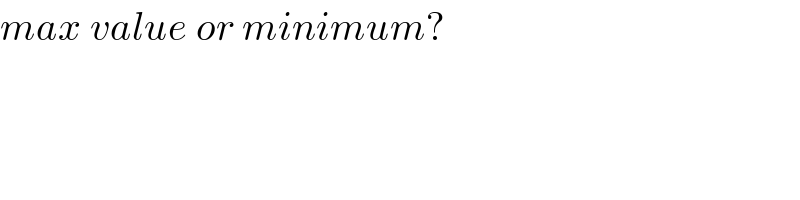
Commented by ajfour last updated on 26/Apr/20

Answered by mr W last updated on 26/Apr/20
![tan^2 [π(x+y)]+cot^2 [π(x+y)]=1+(√((2x)/(x^2 +1))) tan^2 [π(x+y)]+cot^2 [π(x+y)]−2=(√((2x)/(x^2 +1)))−1 {tan [π(x+y)]−cot [π(x+y)]}^2 =(√((2x)/(x^2 +1)))−1 LHS={...}^2 ≥0 RHS=(√((2x)/(x^2 +1)))−1≤0 ⇒LHS=RHS=0 (√((2x)/(x^2 +1)))−1=0 ⇒x=1 tan [π(x+y)]−cot [π(x+y)]=0 tan^2 [π(x+y)]=1 tan [π(x+y)]=±1 ⇒π(x+y)=kπ±(π/4) ⇒x+y=k±(1/4) ⇒y=k−1±(1/4) ⇒y=n±(1/4) with n=any integer or ⇒y=(n/2)+(1/4) with n=any integer](https://www.tinkutara.com/question/Q90798.png)
Commented by mr W last updated on 26/Apr/20

Commented by ajfour last updated on 26/Apr/20
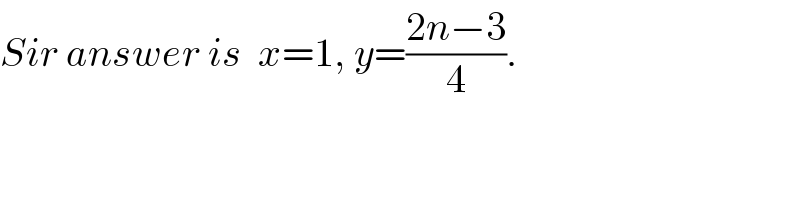
Commented by mr W last updated on 26/Apr/20
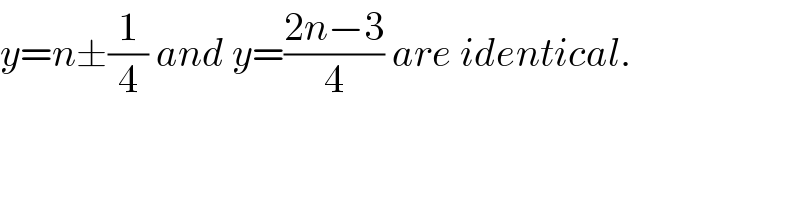
Commented by ajfour last updated on 26/Apr/20

