Menu Close

Solve-for-x-and-y-x-x-y-y-182-i-x-y-y-x-183-ii-

Tinku Tara 0 Comments
Pin




Question Number 56321 by Tawa1 last updated on 14/Mar/19
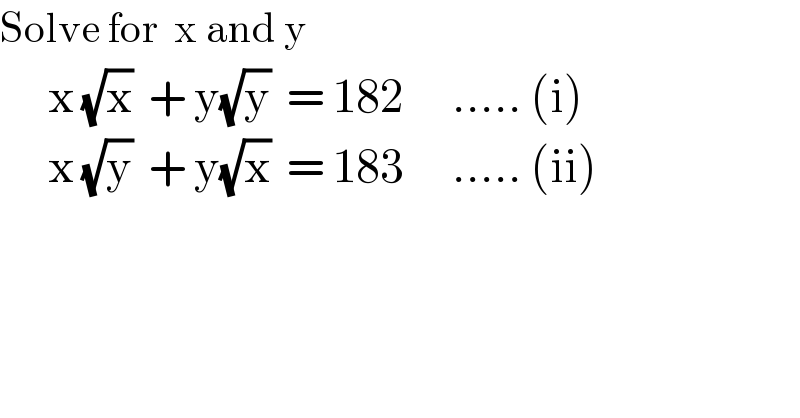
Solve for x and y x (√x) + y(√y) = 182 ..... (i) x (√y) + y(√x) = 183 ..... (ii)
$$\mathrm{Solve}\:\mathrm{for}\:\:\mathrm{x}\:\mathrm{and}\:\mathrm{y} \\ $$$$\:\:\:\:\:\:\mathrm{x}\:\sqrt{\mathrm{x}}\:\:+\:\mathrm{y}\sqrt{\mathrm{y}}\:\:=\:\mathrm{182}\:\:\:\:\:\:…..\:\left(\mathrm{i}\right) \\ $$$$\:\:\:\:\:\:\mathrm{x}\:\sqrt{\mathrm{y}}\:\:+\:\mathrm{y}\sqrt{\mathrm{x}}\:\:=\:\mathrm{183}\:\:\:\:\:\:…..\:\left(\mathrm{ii}\right) \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 14/Mar/19
x=a^2 y=b^2 a^3 +b^3 =182 a^2 b+ab^2 =183 (a+b)^3 −3ab(a+b)=182 (a+b)^3 −3×183=182 (a+b)^3 =182+549=731 (a+b)=(731)^(1/3) ≈9.008→consider 9 a+b=9 ab(a+b)=183 ab=((183)/((731)^(1/3) ))=((183)/(9.008))=20.32 for calculation easy..a+b=9 ab=20 (9−b)b=20 9b−b^2 −20=0 b^2 −9b+20=0 (b−4)(b−5)=0 b=4 and 5 a=5 and 4 x=25 and 16 y=16 and 25
$${x}={a}^{\mathrm{2}} \:\:\:{y}={b}^{\mathrm{2}} \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} =\mathrm{182} \\ $$$${a}^{\mathrm{2}} {b}+{ab}^{\mathrm{2}} =\mathrm{183} \\ $$$$\left({a}+{b}\right)^{\mathrm{3}} −\mathrm{3}{ab}\left({a}+{b}\right)=\mathrm{182} \\ $$$$\left({a}+{b}\right)^{\mathrm{3}} −\mathrm{3}×\mathrm{183}=\mathrm{182} \\ $$$$\left({a}+{b}\right)^{\mathrm{3}} =\mathrm{182}+\mathrm{549}=\mathrm{731} \\ $$$$\left({a}+{b}\right)=\left(\mathrm{731}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \approx\mathrm{9}.\mathrm{008}\rightarrow{consider}\:\mathrm{9} \\ $$$${a}+{b}=\mathrm{9} \\ $$$${ab}\left({a}+{b}\right)=\mathrm{183} \\ $$$${ab}=\frac{\mathrm{183}}{\left(\mathrm{731}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }=\frac{\mathrm{183}}{\mathrm{9}.\mathrm{008}}=\mathrm{20}.\mathrm{32} \\ $$$${for}\:{calculation}\:{easy}..{a}+{b}=\mathrm{9} \\ $$$${ab}=\mathrm{20} \\ $$$$\left(\mathrm{9}−{b}\right){b}=\mathrm{20} \\ $$$$\mathrm{9}{b}−{b}^{\mathrm{2}} −\mathrm{20}=\mathrm{0} \\ $$$${b}^{\mathrm{2}} −\mathrm{9}{b}+\mathrm{20}=\mathrm{0} \\ $$$$\left({b}−\mathrm{4}\right)\left({b}−\mathrm{5}\right)=\mathrm{0} \\ $$$${b}=\mathrm{4}\:{and}\:\:\mathrm{5} \\ $$$${a}=\mathrm{5}\:{and}\:\mathrm{4} \\ $$$${x}=\mathrm{25}\:{and}\:\mathrm{16} \\ $$$${y}=\mathrm{16}\:{and}\:\mathrm{25} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 14/Mar/19
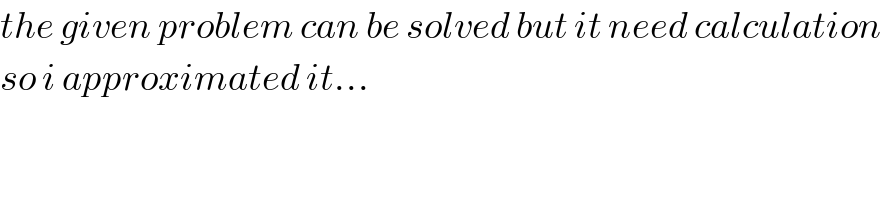
the given problem can be solved but it need calculation so i approximated it...
$${the}\:{given}\:{problem}\:{can}\:{be}\:{solved}\:{but}\:{it}\:{need}\:{calculation} \\ $$$${so}\:{i}\:{approximated}\:{it}… \\ $$
Commented by Tawa1 last updated on 14/Mar/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by behi83417@gmail.com last updated on 14/Mar/19
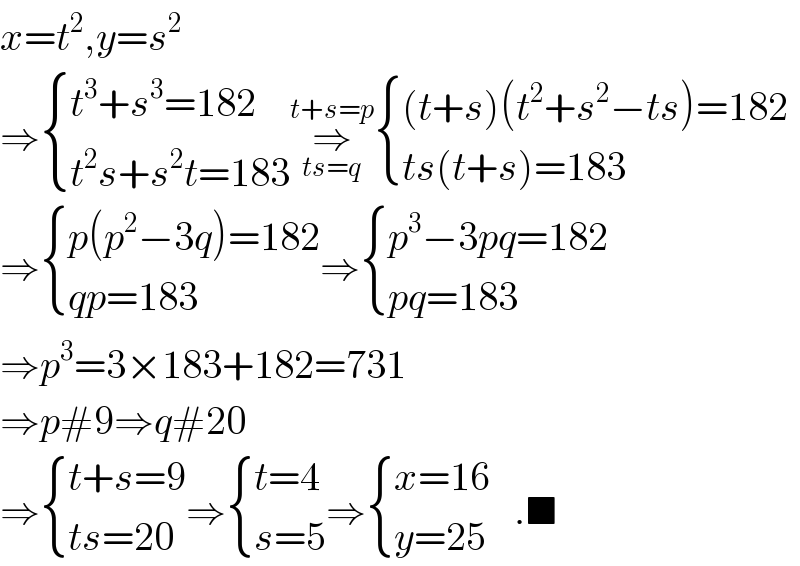
x=t^2 ,y=s^2 ⇒ { ((t^3 +s^3 =182)),((t^2 s+s^2 t=183)) :}⇒_(ts=q) ^(t+s=p) { (((t+s)(t^2 +s^2 −ts)=182)),((ts(t+s)=183)) :} ⇒ { ((p(p^2 −3q)=182)),((qp=183)) :}⇒ { ((p^3 −3pq=182)),((pq=183)) :} ⇒p^3 =3×183+182=731 ⇒p#9⇒q#20 ⇒ { ((t+s=9)),((ts=20)) :}⇒ { ((t=4)),((s=5)) :}⇒ { ((x=16)),((y=25)) :} .■
$${x}={t}^{\mathrm{2}} ,{y}={s}^{\mathrm{2}} \\ $$$$\Rightarrow\begin{cases}{{t}^{\mathrm{3}} +{s}^{\mathrm{3}} =\mathrm{182}}\\{{t}^{\mathrm{2}} {s}+{s}^{\mathrm{2}} {t}=\mathrm{183}}\end{cases}\underset{{ts}={q}} {\overset{{t}+{s}={p}} {\Rightarrow}}\begin{cases}{\left({t}+{s}\right)\left({t}^{\mathrm{2}} +{s}^{\mathrm{2}} −{ts}\right)=\mathrm{182}}\\{{ts}\left({t}+{s}\right)=\mathrm{183}}\end{cases} \\ $$$$\Rightarrow\begin{cases}{{p}\left({p}^{\mathrm{2}} −\mathrm{3}{q}\right)=\mathrm{182}}\\{{qp}=\mathrm{183}}\end{cases}\Rightarrow\begin{cases}{{p}^{\mathrm{3}} −\mathrm{3}{pq}=\mathrm{182}}\\{{pq}=\mathrm{183}}\end{cases} \\ $$$$\Rightarrow{p}^{\mathrm{3}} =\mathrm{3}×\mathrm{183}+\mathrm{182}=\mathrm{731} \\ $$$$\Rightarrow{p}#\mathrm{9}\Rightarrow{q}#\mathrm{20} \\ $$$$\Rightarrow\begin{cases}{{t}+{s}=\mathrm{9}}\\{{ts}=\mathrm{20}}\end{cases}\Rightarrow\begin{cases}{{t}=\mathrm{4}}\\{{s}=\mathrm{5}}\end{cases}\Rightarrow\begin{cases}{{x}=\mathrm{16}}\\{{y}=\mathrm{25}}\end{cases}\:\:\:.\blacksquare \\ $$
Commented by Tawa1 last updated on 14/Mar/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *