Question Number 15786 by tawa tawa last updated on 13/Jun/17
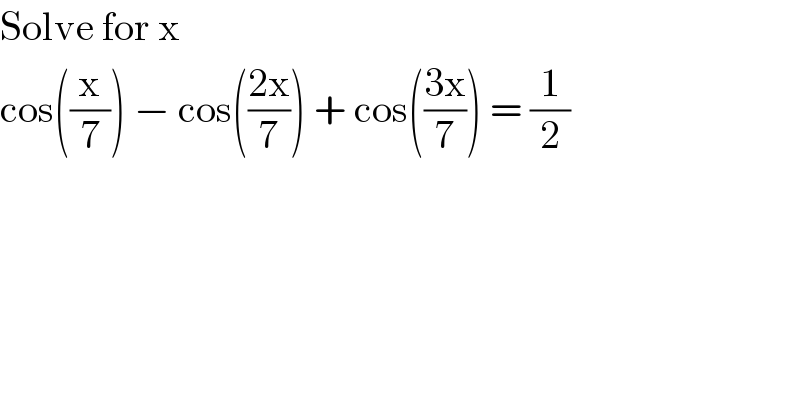
$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{x} \\ $$$$\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{7}}\right)\:−\:\mathrm{cos}\left(\frac{\mathrm{2x}}{\mathrm{7}}\right)\:+\:\mathrm{cos}\left(\frac{\mathrm{3x}}{\mathrm{7}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by tawa tawa last updated on 14/Jun/17
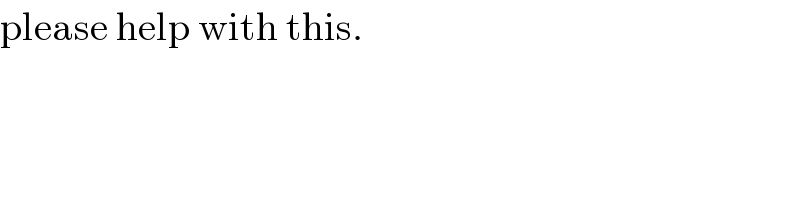
$$\mathrm{please}\:\mathrm{help}\:\mathrm{with}\:\mathrm{this}. \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 14/Jun/17
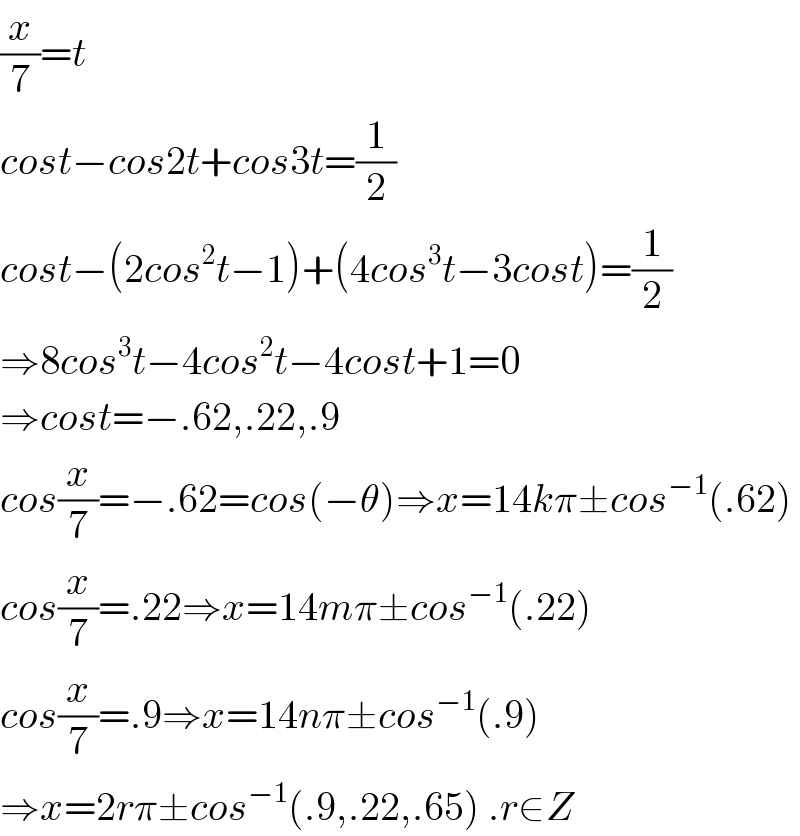
$$\frac{{x}}{\mathrm{7}}={t} \\ $$$${cost}−{cos}\mathrm{2}{t}+{cos}\mathrm{3}{t}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${cost}−\left(\mathrm{2}{cos}^{\mathrm{2}} {t}−\mathrm{1}\right)+\left(\mathrm{4}{cos}^{\mathrm{3}} {t}−\mathrm{3}{cost}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{8}{cos}^{\mathrm{3}} {t}−\mathrm{4}{cos}^{\mathrm{2}} {t}−\mathrm{4}{cost}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{cost}=−.\mathrm{62},.\mathrm{22},.\mathrm{9} \\ $$$${cos}\frac{{x}}{\mathrm{7}}=−.\mathrm{62}={cos}\left(−\theta\right)\Rightarrow{x}=\mathrm{14}{k}\pi\pm{cos}^{−\mathrm{1}} \left(.\mathrm{62}\right) \\ $$$${cos}\frac{{x}}{\mathrm{7}}=.\mathrm{22}\Rightarrow{x}=\mathrm{14}{m}\pi\pm{cos}^{−\mathrm{1}} \left(.\mathrm{22}\right) \\ $$$${cos}\frac{{x}}{\mathrm{7}}=.\mathrm{9}\Rightarrow{x}=\mathrm{14}{n}\pi\pm{cos}^{−\mathrm{1}} \left(.\mathrm{9}\right) \\ $$$$\Rightarrow{x}=\mathrm{2}{r}\pi\pm{cos}^{−\mathrm{1}} \left(.\mathrm{9},.\mathrm{22},.\mathrm{65}\right)\:.{r}\in{Z} \\ $$
Commented by tawa tawa last updated on 14/Jun/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{really}\:\mathrm{appreciate}. \\ $$
