Menu Close

solve-for-x-determinant-1-x-x-2-x-3-1-2-2-2-2-3-1-3-3-2-3-3-1-4-4-2-4-3-0-

Tinku Tara 0 Comments
Pin




Question Number 116578 by bobhans last updated on 05/Oct/20
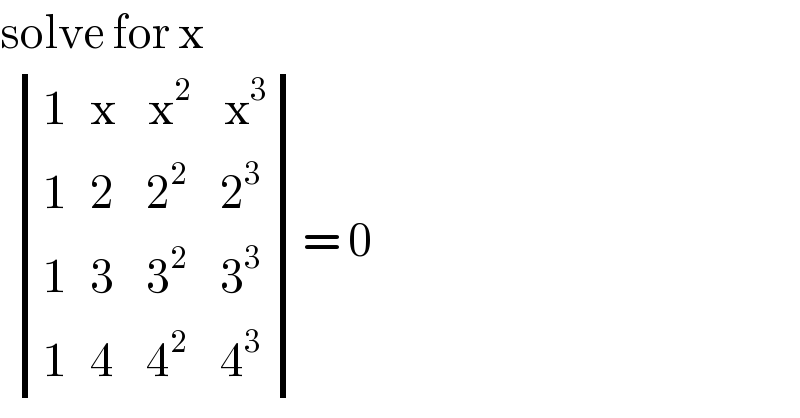
solve for x determinant (((1 x x^2 x^3 )),((1 2 2^2 2^3 )),((1 3 3^2 3^3 )),((1 4 4^2 4^3 )))= 0
$$\mathrm{solve}\:\mathrm{for}\:\mathrm{x}\: \\ $$$$\:\begin{vmatrix}{\mathrm{1}\:\:\:\mathrm{x}\:\:\:\:\mathrm{x}^{\mathrm{2}} \:\:\:\:\mathrm{x}^{\mathrm{3}} }\\{\mathrm{1}\:\:\:\mathrm{2}\:\:\:\:\mathrm{2}^{\mathrm{2}} \:\:\:\:\mathrm{2}^{\mathrm{3}} }\\{\mathrm{1}\:\:\:\mathrm{3}\:\:\:\:\mathrm{3}^{\mathrm{2}} \:\:\:\:\mathrm{3}^{\mathrm{3}} }\\{\mathrm{1}\:\:\:\mathrm{4}\:\:\:\:\mathrm{4}^{\mathrm{2}} \:\:\:\:\mathrm{4}^{\mathrm{3}} }\end{vmatrix}=\:\mathrm{0} \\ $$
Answered by bemath last updated on 05/Oct/20
determinant (((1 0 0 0)),((1 2−x 4−x^2 8−x^3 )),((1 3−x 9−x^2 27−x^3 )),((1 4−x 16−x^2 64−x^3 )))=0 determinant (((2−x 4−x^2 8−x^3 )),((3−x 9−x^2 27−x^3 )),((4−x 16−x^2 64−x^3 )))= 0 (2−x)(3−x)(4−x) determinant (((1 2+x 4+2x+x^2 )),((1 3+x 9+3x+x^2 )),((1 4+x 16+4x+x^2 )))= 0 (2−x)(3−x)(4−x){(12+7x)−(16+12x)+(6+5x)} = 0 2(2−x)(3−x)(4−x)=0 → { ((x=2)),((x=3)),((x=4)) :}
$$\:\begin{vmatrix}{\mathrm{1}\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{1}\:\:\mathrm{2}−\mathrm{x}\:\:\:\:\:\mathrm{4}−\mathrm{x}^{\mathrm{2}} \:\:\:\mathrm{8}−\mathrm{x}^{\mathrm{3}} }\\{\mathrm{1}\:\:\mathrm{3}−\mathrm{x}\:\:\:\:\:\mathrm{9}−\mathrm{x}^{\mathrm{2}} \:\:\:\mathrm{27}−\mathrm{x}^{\mathrm{3}} }\\{\mathrm{1}\:\:\mathrm{4}−\mathrm{x}\:\:\:\mathrm{16}−\mathrm{x}^{\mathrm{2}} \:\:\mathrm{64}−\mathrm{x}^{\mathrm{3}} }\end{vmatrix}=\mathrm{0} \\ $$$$\:\begin{vmatrix}{\mathrm{2}−\mathrm{x}\:\:\:\:\:\mathrm{4}−\mathrm{x}^{\mathrm{2}} \:\:\:\:\mathrm{8}−\mathrm{x}^{\mathrm{3}} }\\{\mathrm{3}−\mathrm{x}\:\:\:\:\mathrm{9}−\mathrm{x}^{\mathrm{2}} \:\:\:\:\mathrm{27}−\mathrm{x}^{\mathrm{3}} }\\{\mathrm{4}−\mathrm{x}\:\:\:\mathrm{16}−\mathrm{x}^{\mathrm{2}} \:\:\:\mathrm{64}−\mathrm{x}^{\mathrm{3}} }\end{vmatrix}=\:\mathrm{0} \\ $$$$\left(\mathrm{2}−\mathrm{x}\right)\left(\mathrm{3}−\mathrm{x}\right)\left(\mathrm{4}−\mathrm{x}\right)\:\begin{vmatrix}{\mathrm{1}\:\:\:\:\mathrm{2}+\mathrm{x}\:\:\:\mathrm{4}+\mathrm{2x}+\mathrm{x}^{\mathrm{2}} }\\{\mathrm{1}\:\:\:\mathrm{3}+\mathrm{x}\:\:\:\:\mathrm{9}+\mathrm{3x}+\mathrm{x}^{\mathrm{2}} }\\{\mathrm{1}\:\:\:\mathrm{4}+\mathrm{x}\:\:\:\mathrm{16}+\mathrm{4x}+\mathrm{x}^{\mathrm{2}} }\end{vmatrix}=\:\mathrm{0} \\ $$$$\left(\mathrm{2}−\mathrm{x}\right)\left(\mathrm{3}−\mathrm{x}\right)\left(\mathrm{4}−\mathrm{x}\right)\left\{\left(\mathrm{12}+\mathrm{7x}\right)−\left(\mathrm{16}+\mathrm{12x}\right)+\left(\mathrm{6}+\mathrm{5x}\right)\right\}\:=\:\mathrm{0} \\ $$$$\mathrm{2}\left(\mathrm{2}−\mathrm{x}\right)\left(\mathrm{3}−\mathrm{x}\right)\left(\mathrm{4}−\mathrm{x}\right)=\mathrm{0} \\ $$$$\rightarrow\begin{cases}{\mathrm{x}=\mathrm{2}}\\{\mathrm{x}=\mathrm{3}}\\{\mathrm{x}=\mathrm{4}}\end{cases} \\ $$
Answered by Olaf last updated on 05/Oct/20
det(A) = −2x^3 +18x^2 −52x+48 det(A) = −2(x−2)(x−3)(x−4) det(A) = 0 ⇔ x = 2 or 3 or 4
$$\mathrm{det}\left(\mathrm{A}\right)\:=\:−\mathrm{2}{x}^{\mathrm{3}} +\mathrm{18}{x}^{\mathrm{2}} −\mathrm{52}{x}+\mathrm{48} \\ $$$$\mathrm{det}\left(\mathrm{A}\right)\:=\:−\mathrm{2}\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right) \\ $$$$\mathrm{det}\left(\mathrm{A}\right)\:=\:\mathrm{0}\:\Leftrightarrow\:{x}\:=\:\mathrm{2}\:\mathrm{or}\:\mathrm{3}\:\mathrm{or}\:\mathrm{4} \\ $$
Answered by 1549442205PVT last updated on 05/Oct/20
A= determinant (((1 x x^2 x^3 )),((1 2 2^2 2^3 )),((1 3 3^2 3^3 )),((1 4 4^2 4^3 )))= 0 ⇔A= determinant ((2,4,8),(3,9,(27)),(4,(16),(64)))−x determinant ((1,4,8),(1,9,(27)),(1,(16),(64))) +x^2 determinant ((1,2,8),(1,3,(27)),(1,4,(64)))−x^3 determinant ((1,2,4),(1,3,9),(1,4,(16))) =48−52x+18x^2 −2x^3 =0 ⇔x^3 −9x^2 +26x−24=0 ⇔(x−2)(x−3)(x−4)=0 ⇔x∈{2,3,4}
$$\mathrm{A}=\:\begin{vmatrix}{\mathrm{1}\:\:\:\mathrm{x}\:\:\:\:\mathrm{x}^{\mathrm{2}} \:\:\:\:\mathrm{x}^{\mathrm{3}} }\\{\mathrm{1}\:\:\:\mathrm{2}\:\:\:\:\mathrm{2}^{\mathrm{2}} \:\:\:\:\mathrm{2}^{\mathrm{3}} }\\{\mathrm{1}\:\:\:\mathrm{3}\:\:\:\:\mathrm{3}^{\mathrm{2}} \:\:\:\:\mathrm{3}^{\mathrm{3}} }\\{\mathrm{1}\:\:\:\mathrm{4}\:\:\:\:\mathrm{4}^{\mathrm{2}} \:\:\:\:\mathrm{4}^{\mathrm{3}} }\end{vmatrix}=\:\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{A}=\begin{vmatrix}{\mathrm{2}}&{\mathrm{4}}&{\mathrm{8}}\\{\mathrm{3}}&{\mathrm{9}}&{\mathrm{27}}\\{\mathrm{4}}&{\mathrm{16}}&{\mathrm{64}}\end{vmatrix}−\mathrm{x}\begin{vmatrix}{\mathrm{1}}&{\mathrm{4}}&{\mathrm{8}}\\{\mathrm{1}}&{\mathrm{9}}&{\mathrm{27}}\\{\mathrm{1}}&{\mathrm{16}}&{\mathrm{64}}\end{vmatrix} \\ $$$$+\mathrm{x}^{\mathrm{2}} \begin{vmatrix}{\mathrm{1}}&{\mathrm{2}}&{\mathrm{8}}\\{\mathrm{1}}&{\mathrm{3}}&{\mathrm{27}}\\{\mathrm{1}}&{\mathrm{4}}&{\mathrm{64}}\end{vmatrix}−\mathrm{x}^{\mathrm{3}} \begin{vmatrix}{\mathrm{1}}&{\mathrm{2}}&{\mathrm{4}}\\{\mathrm{1}}&{\mathrm{3}}&{\mathrm{9}}\\{\mathrm{1}}&{\mathrm{4}}&{\mathrm{16}}\end{vmatrix} \\ $$$$=\mathrm{48}−\mathrm{52x}+\mathrm{18x}^{\mathrm{2}} −\mathrm{2x}^{\mathrm{3}} =\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{x}^{\mathrm{3}} −\mathrm{9x}^{\mathrm{2}} +\mathrm{26x}−\mathrm{24}=\mathrm{0} \\ $$$$\Leftrightarrow\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{x}−\mathrm{3}\right)\left(\mathrm{x}−\mathrm{4}\right)=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{x}\in\left\{\mathrm{2},\mathrm{3},\mathrm{4}\right\} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *