Question Number 181020 by mr W last updated on 20/Nov/22
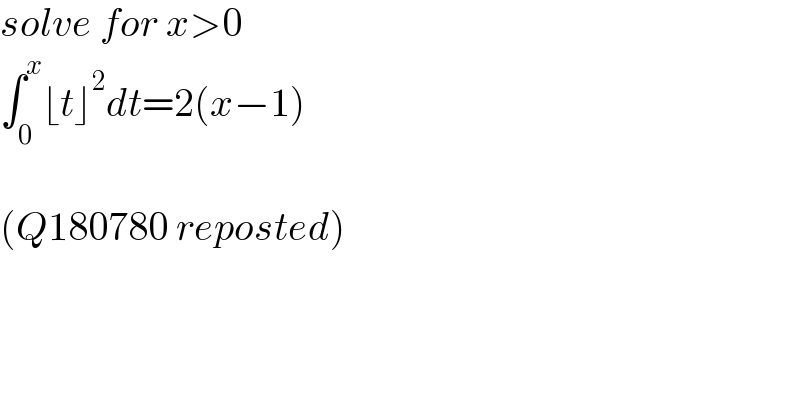
$${solve}\:{for}\:{x}>\mathrm{0} \\ $$$$\int_{\mathrm{0}} ^{{x}} \lfloor{t}\rfloor^{\mathrm{2}} {dt}=\mathrm{2}\left({x}−\mathrm{1}\right) \\ $$$$ \\ $$$$\left({Q}\mathrm{180780}\:{reposted}\right) \\ $$
Answered by mr W last updated on 20/Nov/22
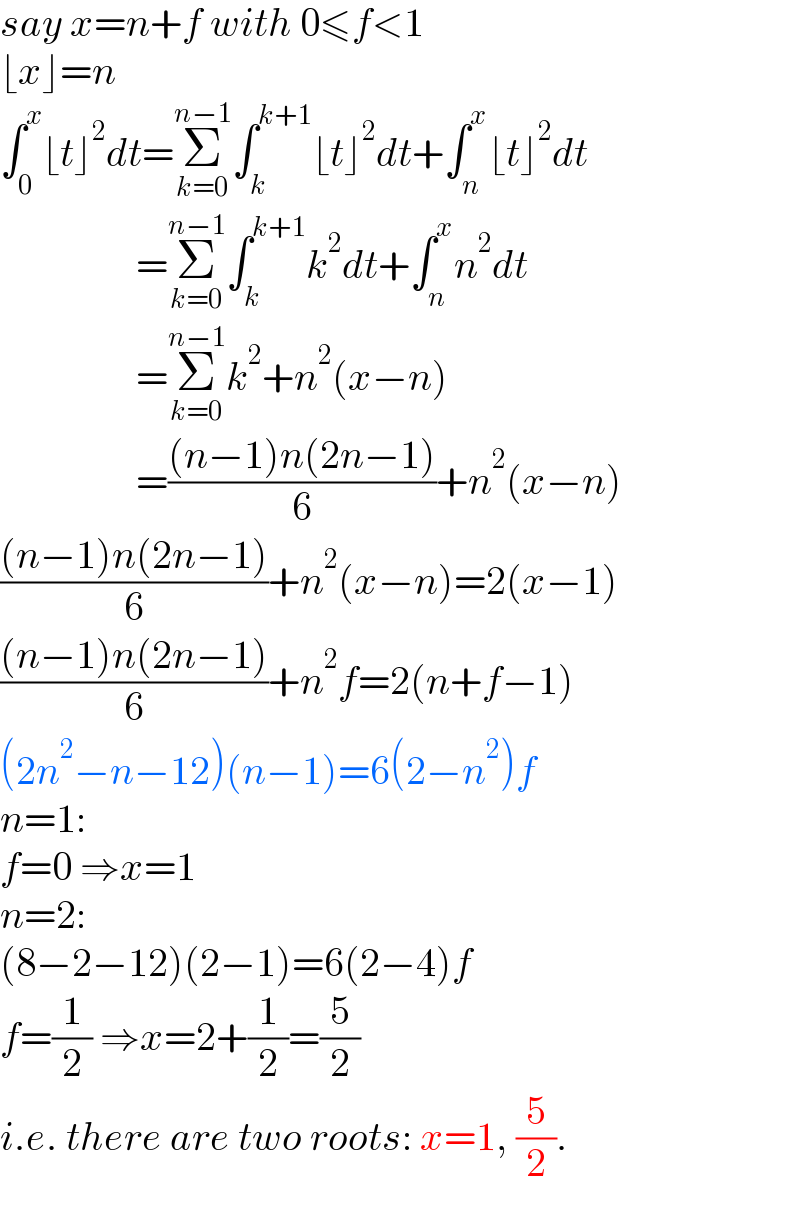
$${say}\:{x}={n}+{f}\:{with}\:\mathrm{0}\leqslant{f}<\mathrm{1} \\ $$$$\lfloor{x}\rfloor={n} \\ $$$$\int_{\mathrm{0}} ^{{x}} \lfloor{t}\rfloor^{\mathrm{2}} {dt}=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\int_{{k}} ^{{k}+\mathrm{1}} \lfloor{t}\rfloor^{\mathrm{2}} {dt}+\int_{{n}} ^{{x}} \lfloor{t}\rfloor^{\mathrm{2}} {dt} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\int_{{k}} ^{{k}+\mathrm{1}} {k}^{\mathrm{2}} {dt}+\int_{{n}} ^{{x}} {n}^{\mathrm{2}} {dt} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{k}^{\mathrm{2}} +{n}^{\mathrm{2}} \left({x}−{n}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\left({n}−\mathrm{1}\right){n}\left(\mathrm{2}{n}−\mathrm{1}\right)}{\mathrm{6}}+{n}^{\mathrm{2}} \left({x}−{n}\right) \\ $$$$\frac{\left({n}−\mathrm{1}\right){n}\left(\mathrm{2}{n}−\mathrm{1}\right)}{\mathrm{6}}+{n}^{\mathrm{2}} \left({x}−{n}\right)=\mathrm{2}\left({x}−\mathrm{1}\right) \\ $$$$\frac{\left({n}−\mathrm{1}\right){n}\left(\mathrm{2}{n}−\mathrm{1}\right)}{\mathrm{6}}+{n}^{\mathrm{2}} {f}=\mathrm{2}\left({n}+{f}−\mathrm{1}\right) \\ $$$$\left(\mathrm{2}{n}^{\mathrm{2}} −{n}−\mathrm{12}\right)\left({n}−\mathrm{1}\right)=\mathrm{6}\left(\mathrm{2}−{n}^{\mathrm{2}} \right){f} \\ $$$${n}=\mathrm{1}:\: \\ $$$${f}=\mathrm{0}\:\Rightarrow{x}=\mathrm{1} \\ $$$${n}=\mathrm{2}: \\ $$$$\left(\mathrm{8}−\mathrm{2}−\mathrm{12}\right)\left(\mathrm{2}−\mathrm{1}\right)=\mathrm{6}\left(\mathrm{2}−\mathrm{4}\right){f} \\ $$$${f}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{x}=\mathrm{2}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$${i}.{e}.\:{there}\:{are}\:{two}\:{roots}:\:{x}=\mathrm{1},\:\frac{\mathrm{5}}{\mathrm{2}}. \\ $$
