Question Number 94855 by mathocean1 last updated on 21/May/20
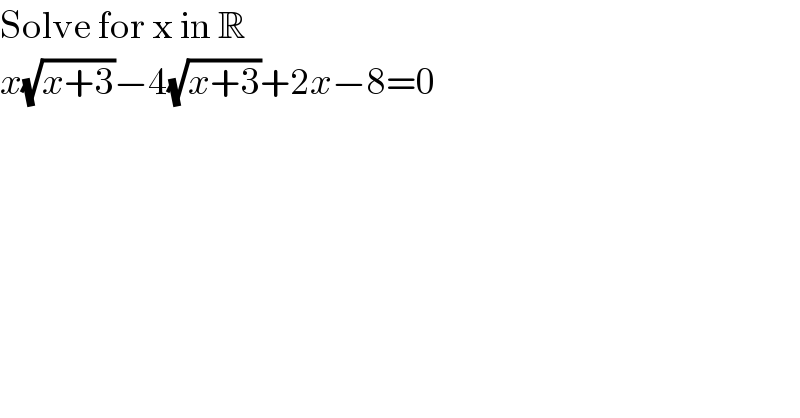
$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{x}\:\mathrm{in}\:\mathbb{R} \\ $$$${x}\sqrt{{x}+\mathrm{3}}−\mathrm{4}\sqrt{{x}+\mathrm{3}}+\mathrm{2}{x}−\mathrm{8}=\mathrm{0} \\ $$
Answered by ElOuafi last updated on 21/May/20
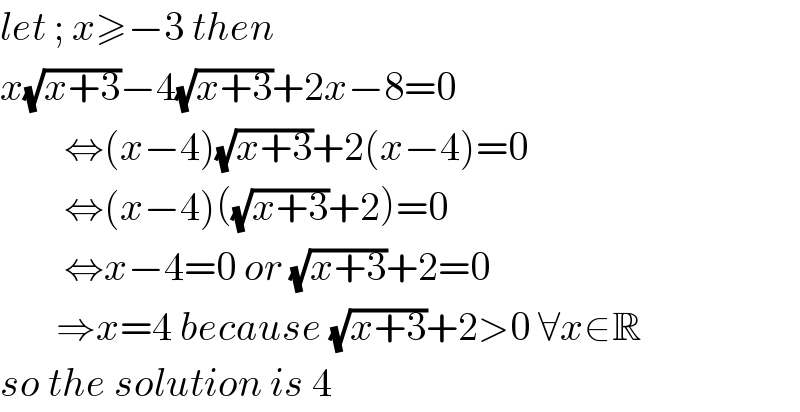
$${let}\:;\:{x}\geqslant−\mathrm{3}\:{then}\: \\ $$$${x}\sqrt{{x}+\mathrm{3}}−\mathrm{4}\sqrt{{x}+\mathrm{3}}+\mathrm{2}{x}−\mathrm{8}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\Leftrightarrow\left({x}−\mathrm{4}\right)\sqrt{{x}+\mathrm{3}}+\mathrm{2}\left({x}−\mathrm{4}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\Leftrightarrow\left({x}−\mathrm{4}\right)\left(\sqrt{{x}+\mathrm{3}}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\Leftrightarrow{x}−\mathrm{4}=\mathrm{0}\:{or}\:\sqrt{{x}+\mathrm{3}}+\mathrm{2}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\Rightarrow{x}=\mathrm{4}\:{because}\:\sqrt{{x}+\mathrm{3}}+\mathrm{2}>\mathrm{0}\:\forall{x}\in\mathbb{R} \\ $$$${so}\:{the}\:{solution}\:{is}\:\mathrm{4} \\ $$
Commented by mathocean1 last updated on 21/May/20

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}! \\ $$
