Menu Close

solve-for-x-R-12-4x-x-2-1-4-1-8x-2x-2-2x-2-8x-13-

Tinku Tara 0 Comments
Pin




Question Number 174427 by mnjuly1970 last updated on 31/Jul/22
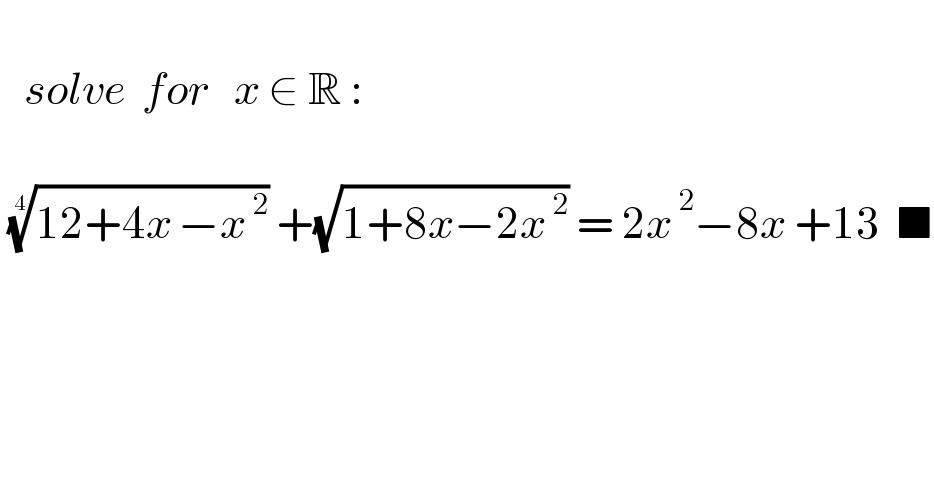
solve for x ∈ R : ((12+4x^ −x^( 2) ))^(1/4) +(√(1+8x−2x^( 2) )) = 2x^( 2) −8x +13 ■
$$ \\ $$$$\:\:\:{solve}\:\:{for}\:\:\:{x}\:\in\:\mathbb{R}\:: \\ $$$$ \\ $$$$\:\sqrt[{\mathrm{4}}]{\mathrm{12}+\mathrm{4}{x}^{\:} −{x}^{\:\mathrm{2}} }\:+\sqrt{\mathrm{1}+\mathrm{8}{x}−\mathrm{2}{x}^{\:\mathrm{2}} }\:=\:\mathrm{2}{x}^{\:\mathrm{2}} −\mathrm{8}{x}\:+\mathrm{13}\:\:\blacksquare \\ $$$$ \\ $$$$ \\ $$
Answered by MJS_new last updated on 02/Aug/22
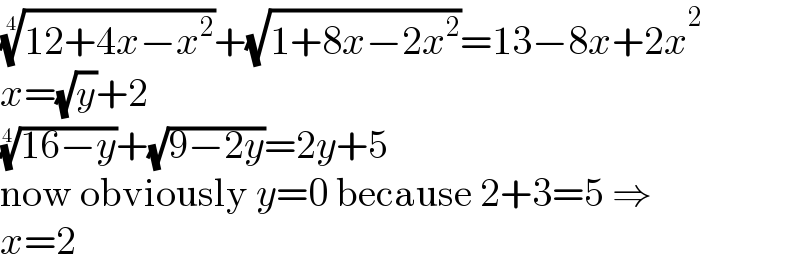
((12+4x−x^2 ))^(1/4) +(√(1+8x−2x^2 ))=13−8x+2x^2 x=(√y)+2 ((16−y))^(1/4) +(√(9−2y))=2y+5 now obviously y=0 because 2+3=5 ⇒ x=2
$$\sqrt[{\mathrm{4}}]{\mathrm{12}+\mathrm{4}{x}−{x}^{\mathrm{2}} }+\sqrt{\mathrm{1}+\mathrm{8}{x}−\mathrm{2}{x}^{\mathrm{2}} }=\mathrm{13}−\mathrm{8}{x}+\mathrm{2}{x}^{\mathrm{2}} \\ $$$${x}=\sqrt{{y}}+\mathrm{2} \\ $$$$\sqrt[{\mathrm{4}}]{\mathrm{16}−{y}}+\sqrt{\mathrm{9}−\mathrm{2}{y}}=\mathrm{2}{y}+\mathrm{5} \\ $$$$\mathrm{now}\:\mathrm{obviously}\:{y}=\mathrm{0}\:\mathrm{because}\:\mathrm{2}+\mathrm{3}=\mathrm{5}\:\Rightarrow \\ $$$${x}=\mathrm{2} \\ $$
Commented by mnjuly1970 last updated on 01/Aug/22
thanks alot sir
$${thanks}\:{alot}\:{sir} \\ $$
Commented by MJS_new last updated on 01/Aug/22
I don′t think there are other solutions ∈C Sirs, you have to test your solutions with the given equation!
$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{there}\:\mathrm{are}\:\mathrm{other}\:\mathrm{solutions}\:\in\mathbb{C} \\ $$$$\mathrm{Sirs},\:\mathrm{you}\:\mathrm{have}\:\mathrm{to}\:\mathrm{test}\:\mathrm{your}\:\mathrm{solutions}\:\mathrm{with} \\ $$$$\mathrm{the}\:\mathrm{given}\:\mathrm{equation}! \\ $$
Commented by MJS_new last updated on 02/Aug/22
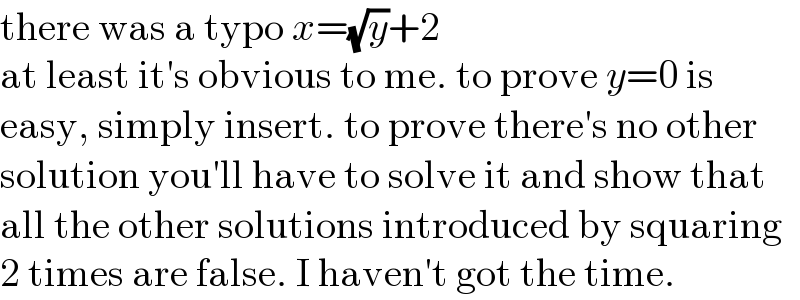
there was a typo x=(√y)+2 at least it′s obvious to me. to prove y=0 is easy, simply insert. to prove there′s no other solution you′ll have to solve it and show that all the other solutions introduced by squaring 2 times are false. I haven′t got the time.
$$\mathrm{there}\:\mathrm{was}\:\mathrm{a}\:\mathrm{typo}\:{x}=\sqrt{{y}}+\mathrm{2} \\ $$$$\mathrm{at}\:\mathrm{least}\:\mathrm{it}'\mathrm{s}\:\mathrm{obvious}\:\mathrm{to}\:\mathrm{me}.\:\mathrm{to}\:\mathrm{prove}\:{y}=\mathrm{0}\:\mathrm{is} \\ $$$$\mathrm{easy},\:\mathrm{simply}\:\mathrm{insert}.\:\mathrm{to}\:\mathrm{prove}\:\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{other} \\ $$$$\mathrm{solution}\:\mathrm{you}'\mathrm{ll}\:\mathrm{have}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{it}\:\mathrm{and}\:\mathrm{show}\:\mathrm{that} \\ $$$$\mathrm{all}\:\mathrm{the}\:\mathrm{other}\:\mathrm{solutions}\:\mathrm{introduced}\:\mathrm{by}\:\mathrm{squaring} \\ $$$$\mathrm{2}\:\mathrm{times}\:\mathrm{are}\:\mathrm{false}.\:\mathrm{I}\:\mathrm{haven}'\mathrm{t}\:\mathrm{got}\:\mathrm{the}\:\mathrm{time}. \\ $$
Answered by behi834171 last updated on 01/Aug/22
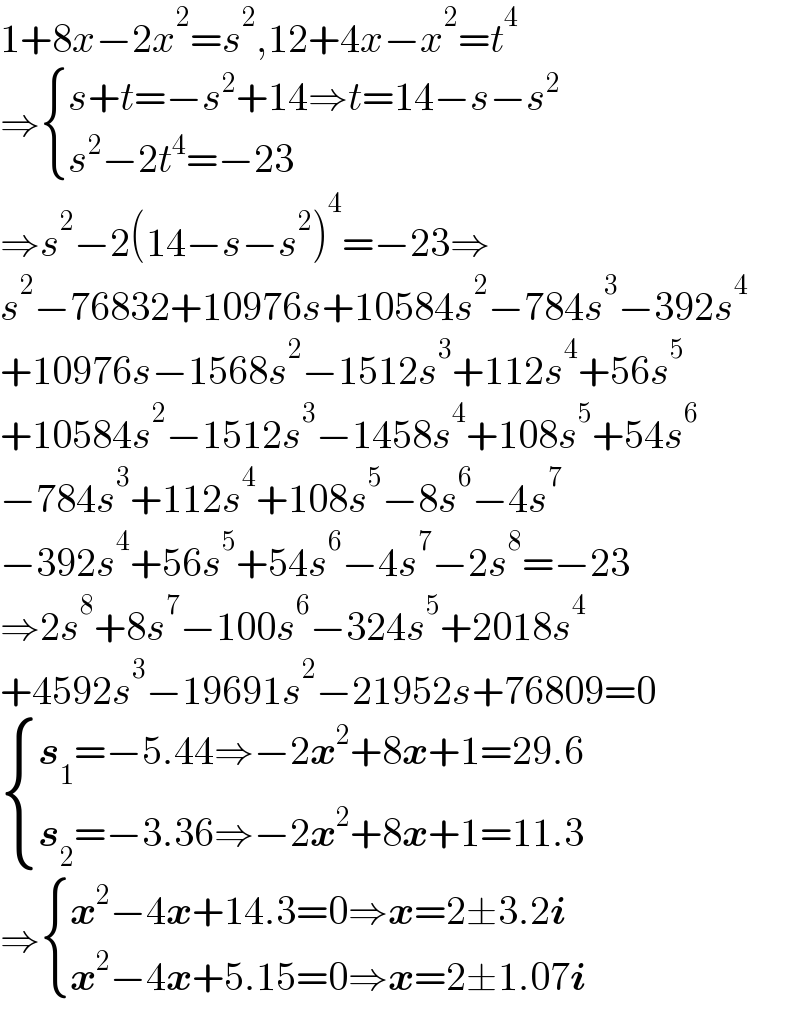
1+8x−2x^2 =s^2 ,12+4x−x^2 =t^4 ⇒ { ((s+t=−s^2 +14⇒t=14−s−s^2 )),((s^2 −2t^4 =−23)) :} ⇒s^2 −2(14−s−s^2 )^4 =−23⇒ s^2 −76832+10976s+10584s^2 −784s^3 −392s^4 +10976s−1568s^2 −1512s^3 +112s^4 +56s^5 +10584s^2 −1512s^3 −1458s^4 +108s^5 +54s^6 −784s^3 +112s^4 +108s^5 −8s^6 −4s^7 −392s^4 +56s^5 +54s^6 −4s^7 −2s^8 =−23 ⇒2s^8 +8s^7 −100s^6 −324s^5 +2018s^4 +4592s^3 −19691s^2 −21952s+76809=0 { ((s_1 =−5.44⇒−2x^2 +8x+1=29.6)),((s_2 =−3.36⇒−2x^2 +8x+1=11.3)) :} ⇒ { ((x^2 −4x+14.3=0⇒x=2±3.2i)),((x^2 −4x+5.15=0⇒x=2±1.07i)) :}
$$\mathrm{1}+\mathrm{8}{x}−\mathrm{2}{x}^{\mathrm{2}} ={s}^{\mathrm{2}} ,\mathrm{12}+\mathrm{4}{x}−{x}^{\mathrm{2}} ={t}^{\mathrm{4}} \\ $$$$\Rightarrow\begin{cases}{{s}+{t}=−{s}^{\mathrm{2}} +\mathrm{14}\Rightarrow{t}=\mathrm{14}−{s}−{s}^{\mathrm{2}} }\\{{s}^{\mathrm{2}} −\mathrm{2}{t}^{\mathrm{4}} =−\mathrm{23}}\end{cases} \\ $$$$\Rightarrow{s}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{14}−{s}−{s}^{\mathrm{2}} \right)^{\mathrm{4}} =−\mathrm{23}\Rightarrow \\ $$$${s}^{\mathrm{2}} −\mathrm{76832}+\mathrm{10976}{s}+\mathrm{10584}{s}^{\mathrm{2}} −\mathrm{784}{s}^{\mathrm{3}} −\mathrm{392}{s}^{\mathrm{4}} \\ $$$$+\mathrm{10976}{s}−\mathrm{1568}{s}^{\mathrm{2}} −\mathrm{1512}{s}^{\mathrm{3}} +\mathrm{112}{s}^{\mathrm{4}} +\mathrm{56}{s}^{\mathrm{5}} \\ $$$$+\mathrm{10584}{s}^{\mathrm{2}} −\mathrm{1512}{s}^{\mathrm{3}} −\mathrm{1458}{s}^{\mathrm{4}} +\mathrm{108}{s}^{\mathrm{5}} +\mathrm{54}{s}^{\mathrm{6}} \\ $$$$−\mathrm{784}{s}^{\mathrm{3}} +\mathrm{112}{s}^{\mathrm{4}} +\mathrm{108}{s}^{\mathrm{5}} −\mathrm{8}{s}^{\mathrm{6}} −\mathrm{4}{s}^{\mathrm{7}} \\ $$$$−\mathrm{392}{s}^{\mathrm{4}} +\mathrm{56}{s}^{\mathrm{5}} +\mathrm{54}{s}^{\mathrm{6}} −\mathrm{4}{s}^{\mathrm{7}} −\mathrm{2}{s}^{\mathrm{8}} =−\mathrm{23} \\ $$$$\Rightarrow\mathrm{2}{s}^{\mathrm{8}} +\mathrm{8}{s}^{\mathrm{7}} −\mathrm{100}{s}^{\mathrm{6}} −\mathrm{324}{s}^{\mathrm{5}} +\mathrm{2018}{s}^{\mathrm{4}} \\ $$$$+\mathrm{4592}{s}^{\mathrm{3}} −\mathrm{19691}{s}^{\mathrm{2}} −\mathrm{21952}{s}+\mathrm{76809}=\mathrm{0} \\ $$$$\begin{cases}{\boldsymbol{{s}}_{\mathrm{1}} =−\mathrm{5}.\mathrm{44}\Rightarrow−\mathrm{2}\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{8}\boldsymbol{{x}}+\mathrm{1}=\mathrm{29}.\mathrm{6}}\\{\boldsymbol{{s}}_{\mathrm{2}} =−\mathrm{3}.\mathrm{36}\Rightarrow−\mathrm{2}\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{8}\boldsymbol{{x}}+\mathrm{1}=\mathrm{11}.\mathrm{3}}\end{cases} \\ $$$$\Rightarrow\begin{cases}{\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{4}\boldsymbol{{x}}+\mathrm{14}.\mathrm{3}=\mathrm{0}\Rightarrow\boldsymbol{{x}}=\mathrm{2}\pm\mathrm{3}.\mathrm{2}\boldsymbol{{i}}}\\{\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{4}\boldsymbol{{x}}+\mathrm{5}.\mathrm{15}=\mathrm{0}\Rightarrow\boldsymbol{{x}}=\mathrm{2}\pm\mathrm{1}.\mathrm{07}\boldsymbol{{i}}}\end{cases} \\ $$
Commented by dragan91 last updated on 01/Aug/22
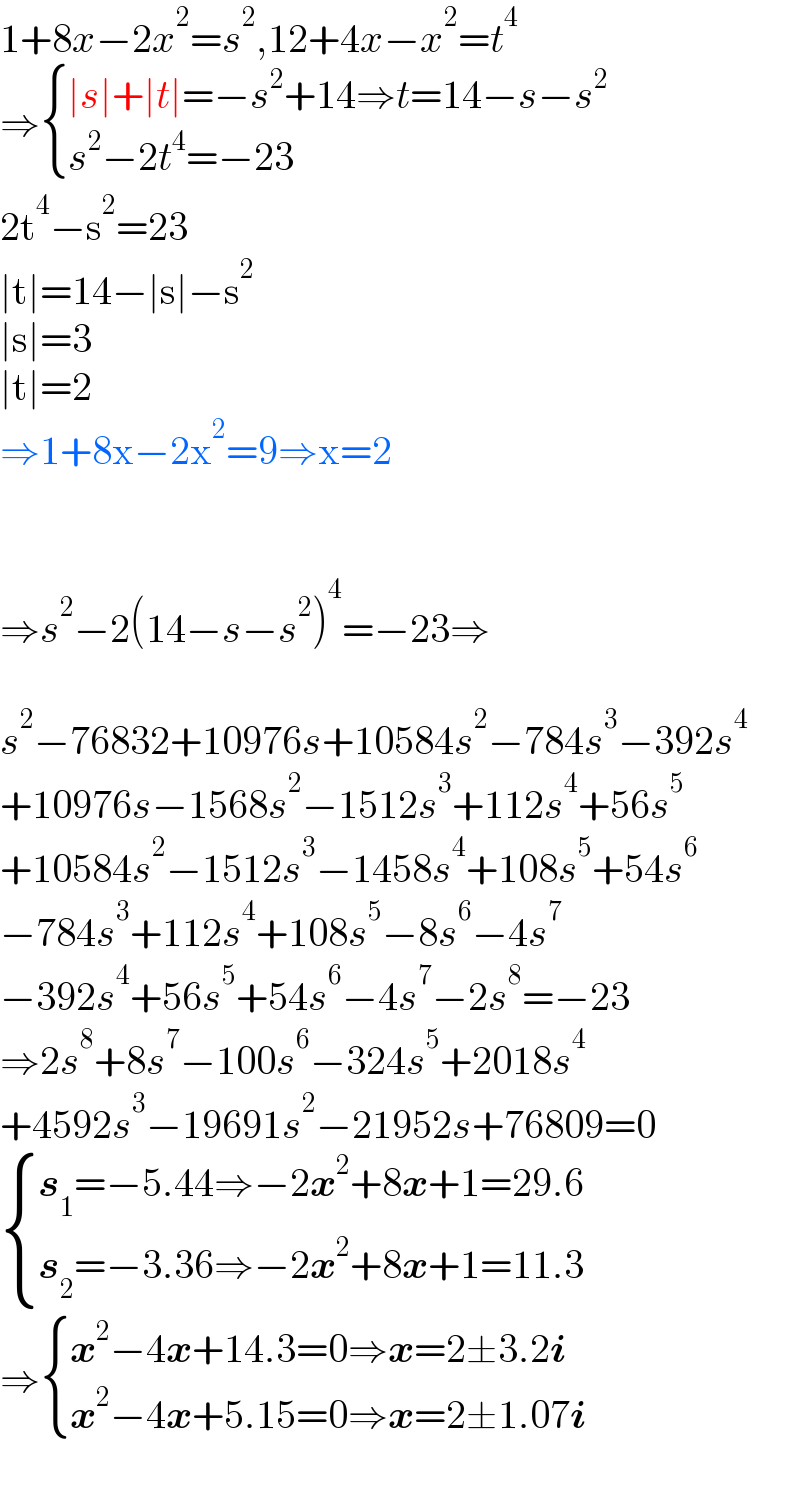
1+8x−2x^2 =s^2 ,12+4x−x^2 =t^4 ⇒ { ((∣s∣+∣t∣=−s^2 +14⇒t=14−s−s^2 )),((s^2 −2t^4 =−23)) :} 2t^4 −s^2 =23 ∣t∣=14−∣s∣−s^2 ∣s∣=3 ∣t∣=2 ⇒1+8x−2x^2 =9⇒x=2 ⇒s^2 −2(14−s−s^2 )^4 =−23⇒ s^2 −76832+10976s+10584s^2 −784s^3 −392s^4 +10976s−1568s^2 −1512s^3 +112s^4 +56s^5 +10584s^2 −1512s^3 −1458s^4 +108s^5 +54s^6 −784s^3 +112s^4 +108s^5 −8s^6 −4s^7 −392s^4 +56s^5 +54s^6 −4s^7 −2s^8 =−23 ⇒2s^8 +8s^7 −100s^6 −324s^5 +2018s^4 +4592s^3 −19691s^2 −21952s+76809=0 { ((s_1 =−5.44⇒−2x^2 +8x+1=29.6)),((s_2 =−3.36⇒−2x^2 +8x+1=11.3)) :} ⇒ { ((x^2 −4x+14.3=0⇒x=2±3.2i)),((x^2 −4x+5.15=0⇒x=2±1.07i)) :}
$$\mathrm{1}+\mathrm{8}{x}−\mathrm{2}{x}^{\mathrm{2}} ={s}^{\mathrm{2}} ,\mathrm{12}+\mathrm{4}{x}−{x}^{\mathrm{2}} ={t}^{\mathrm{4}} \\ $$$$\Rightarrow\begin{cases}{\mid{s}\mid+\mid{t}\mid=−{s}^{\mathrm{2}} +\mathrm{14}\Rightarrow{t}=\mathrm{14}−{s}−{s}^{\mathrm{2}} }\\{{s}^{\mathrm{2}} −\mathrm{2}{t}^{\mathrm{4}} =−\mathrm{23}}\end{cases} \\ $$$$\mathrm{2t}^{\mathrm{4}} −\mathrm{s}^{\mathrm{2}} =\mathrm{23} \\ $$$$\mid\mathrm{t}\mid=\mathrm{14}−\mid\mathrm{s}\mid−\mathrm{s}^{\mathrm{2}} \\ $$$$\mid\mathrm{s}\mid=\mathrm{3} \\ $$$$\mid\mathrm{t}\mid=\mathrm{2} \\ $$$$\Rightarrow\mathrm{1}+\mathrm{8x}−\mathrm{2x}^{\mathrm{2}} =\mathrm{9}\Rightarrow\mathrm{x}=\mathrm{2} \\ $$$$ \\ $$$$ \\ $$$$\Rightarrow{s}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{14}−{s}−{s}^{\mathrm{2}} \right)^{\mathrm{4}} =−\mathrm{23}\Rightarrow \\ $$$$ \\ $$$${s}^{\mathrm{2}} −\mathrm{76832}+\mathrm{10976}{s}+\mathrm{10584}{s}^{\mathrm{2}} −\mathrm{784}{s}^{\mathrm{3}} −\mathrm{392}{s}^{\mathrm{4}} \\ $$$$+\mathrm{10976}{s}−\mathrm{1568}{s}^{\mathrm{2}} −\mathrm{1512}{s}^{\mathrm{3}} +\mathrm{112}{s}^{\mathrm{4}} +\mathrm{56}{s}^{\mathrm{5}} \\ $$$$+\mathrm{10584}{s}^{\mathrm{2}} −\mathrm{1512}{s}^{\mathrm{3}} −\mathrm{1458}{s}^{\mathrm{4}} +\mathrm{108}{s}^{\mathrm{5}} +\mathrm{54}{s}^{\mathrm{6}} \\ $$$$−\mathrm{784}{s}^{\mathrm{3}} +\mathrm{112}{s}^{\mathrm{4}} +\mathrm{108}{s}^{\mathrm{5}} −\mathrm{8}{s}^{\mathrm{6}} −\mathrm{4}{s}^{\mathrm{7}} \\ $$$$−\mathrm{392}{s}^{\mathrm{4}} +\mathrm{56}{s}^{\mathrm{5}} +\mathrm{54}{s}^{\mathrm{6}} −\mathrm{4}{s}^{\mathrm{7}} −\mathrm{2}{s}^{\mathrm{8}} =−\mathrm{23} \\ $$$$\Rightarrow\mathrm{2}{s}^{\mathrm{8}} +\mathrm{8}{s}^{\mathrm{7}} −\mathrm{100}{s}^{\mathrm{6}} −\mathrm{324}{s}^{\mathrm{5}} +\mathrm{2018}{s}^{\mathrm{4}} \\ $$$$+\mathrm{4592}{s}^{\mathrm{3}} −\mathrm{19691}{s}^{\mathrm{2}} −\mathrm{21952}{s}+\mathrm{76809}=\mathrm{0} \\ $$$$\begin{cases}{\boldsymbol{{s}}_{\mathrm{1}} =−\mathrm{5}.\mathrm{44}\Rightarrow−\mathrm{2}\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{8}\boldsymbol{{x}}+\mathrm{1}=\mathrm{29}.\mathrm{6}}\\{\boldsymbol{{s}}_{\mathrm{2}} =−\mathrm{3}.\mathrm{36}\Rightarrow−\mathrm{2}\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{8}\boldsymbol{{x}}+\mathrm{1}=\mathrm{11}.\mathrm{3}}\end{cases} \\ $$$$\Rightarrow\begin{cases}{\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{4}\boldsymbol{{x}}+\mathrm{14}.\mathrm{3}=\mathrm{0}\Rightarrow\boldsymbol{{x}}=\mathrm{2}\pm\mathrm{3}.\mathrm{2}\boldsymbol{{i}}}\\{\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{4}\boldsymbol{{x}}+\mathrm{5}.\mathrm{15}=\mathrm{0}\Rightarrow\boldsymbol{{x}}=\mathrm{2}\pm\mathrm{1}.\mathrm{07}\boldsymbol{{i}}}\end{cases} \\ $$
Commented by MJS_new last updated on 02/Aug/22
you must test these solutions, they are false
$$\mathrm{you}\:\mathrm{must}\:\mathrm{test}\:\mathrm{these}\:\mathrm{solutions},\:\mathrm{they}\:\mathrm{are}\:\mathrm{false} \\ $$
Commented by Tawa11 last updated on 02/Aug/22
Great sirs
$$\mathrm{Great}\:\mathrm{sirs} \\ $$
Answered by dragan91 last updated on 03/Aug/22
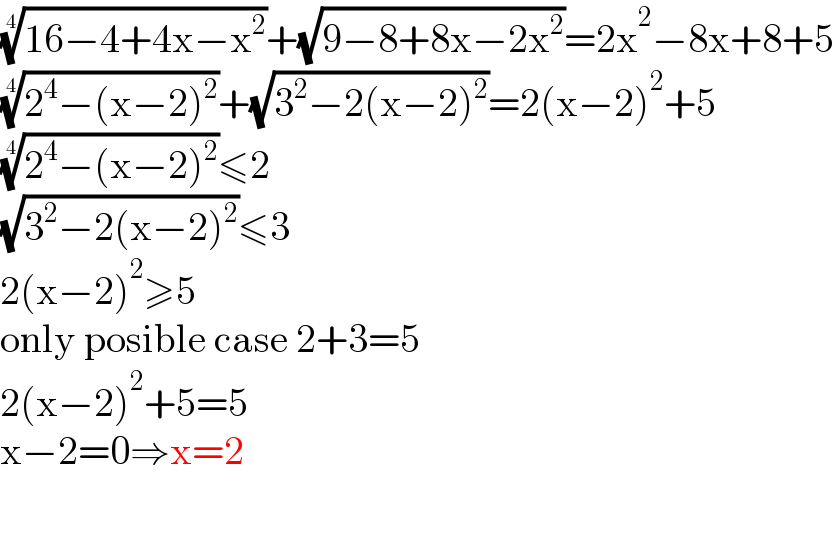
((16−4+4x−x^2 ))^(1/4) +(√(9−8+8x−2x^2 ))=2x^2 −8x+8+5 ((2^4 −(x−2)^2 ))^(1/4) +(√(3^2 −2(x−2)^2 ))=2(x−2)^2 +5 ((2^4 −(x−2)^2 ))^(1/4) ≤2 (√(3^2 −2(x−2)^2 ))≤3 2(x−2)^2 ≥5 only posible case 2+3=5 2(x−2)^2 +5=5 x−2=0⇒x=2
$$\sqrt[{\mathrm{4}}]{\mathrm{16}−\mathrm{4}+\mathrm{4x}−\mathrm{x}^{\mathrm{2}} }+\sqrt{\mathrm{9}−\mathrm{8}+\mathrm{8x}−\mathrm{2x}^{\mathrm{2}} }=\mathrm{2x}^{\mathrm{2}} −\mathrm{8x}+\mathrm{8}+\mathrm{5} \\ $$$$\sqrt[{\mathrm{4}}]{\mathrm{2}^{\mathrm{4}} −\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} }+\sqrt{\mathrm{3}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} }=\mathrm{2}\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{5} \\ $$$$\sqrt[{\mathrm{4}}]{\mathrm{2}^{\mathrm{4}} −\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} }\leqslant\mathrm{2} \\ $$$$\sqrt{\mathrm{3}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} }\leqslant\mathrm{3} \\ $$$$\mathrm{2}\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} \geqslant\mathrm{5} \\ $$$$\mathrm{only}\:\mathrm{posible}\:\mathrm{case}\:\mathrm{2}+\mathrm{3}=\mathrm{5} \\ $$$$\mathrm{2}\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{5}=\mathrm{5} \\ $$$$\mathrm{x}−\mathrm{2}=\mathrm{0}\Rightarrow\mathrm{x}=\mathrm{2} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *