Menu Close

solve-for-x-R-5x-3-3x-5-x-4-

Tinku Tara 0 Comments
Pin




Question Number 173574 by mr W last updated on 13/Jul/22
solve for x∈R ((5x−3)/(3x−5))=x^4
$${solve}\:{for}\:{x}\in{R} \\ $$$$\frac{\mathrm{5}{x}−\mathrm{3}}{\mathrm{3}{x}−\mathrm{5}}={x}^{\mathrm{4}} \\ $$
Commented by kaivan.ahmadi last updated on 14/Jul/22
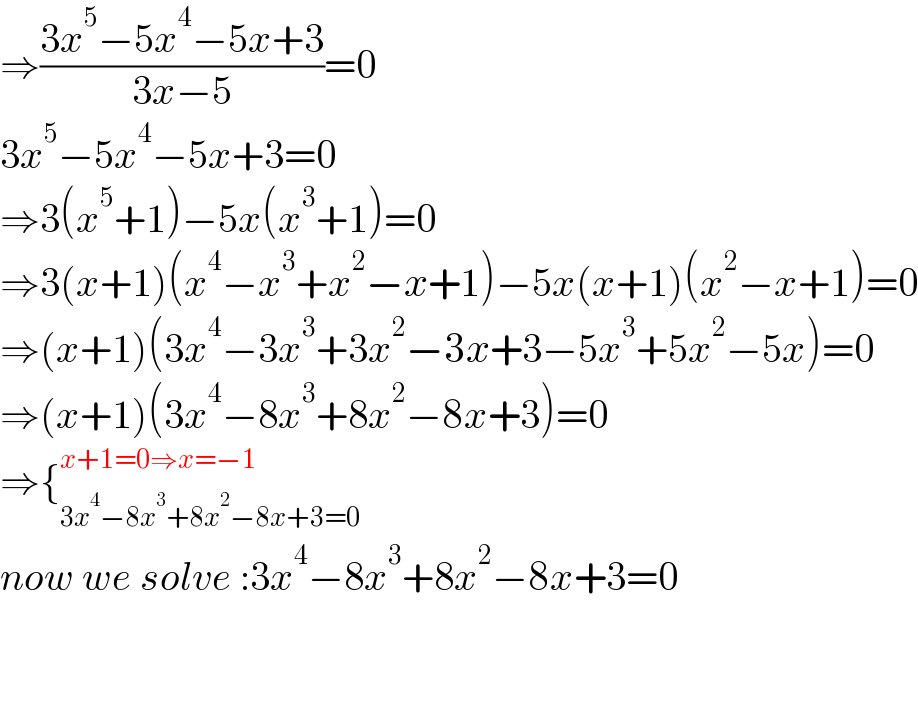
⇒((3x^5 −5x^4 −5x+3)/(3x−5))=0 3x^5 −5x^4 −5x+3=0 ⇒3(x^5 +1)−5x(x^3 +1)=0 ⇒3(x+1)(x^4 −x^3 +x^2 −x+1)−5x(x+1)(x^2 −x+1)=0 ⇒(x+1)(3x^4 −3x^3 +3x^2 −3x+3−5x^3 +5x^2 −5x)=0 ⇒(x+1)(3x^4 −8x^3 +8x^2 −8x+3)=0 ⇒{_(3x^4 −8x^3 +8x^2 −8x+3=0) ^(x+1=0⇒x=−1) now we solve :3x^4 −8x^3 +8x^2 −8x+3=0
$$\Rightarrow\frac{\mathrm{3}{x}^{\mathrm{5}} −\mathrm{5}{x}^{\mathrm{4}} −\mathrm{5}{x}+\mathrm{3}}{\mathrm{3}{x}−\mathrm{5}}=\mathrm{0} \\ $$$$\mathrm{3}{x}^{\mathrm{5}} −\mathrm{5}{x}^{\mathrm{4}} −\mathrm{5}{x}+\mathrm{3}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{3}\left({x}^{\mathrm{5}} +\mathrm{1}\right)−\mathrm{5}{x}\left({x}^{\mathrm{3}} +\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{3}\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{4}} −{x}^{\mathrm{3}} +{x}^{\mathrm{2}} −{x}+\mathrm{1}\right)−\mathrm{5}{x}\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\left({x}+\mathrm{1}\right)\left(\mathrm{3}{x}^{\mathrm{4}} −\mathrm{3}{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}−\mathrm{5}{x}^{\mathrm{3}} +\mathrm{5}{x}^{\mathrm{2}} −\mathrm{5}{x}\right)=\mathrm{0} \\ $$$$\Rightarrow\left({x}+\mathrm{1}\right)\left(\mathrm{3}{x}^{\mathrm{4}} −\mathrm{8}{x}^{\mathrm{3}} +\mathrm{8}{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{3}\right)=\mathrm{0} \\ $$$$\Rightarrow\left\{_{\mathrm{3}{x}^{\mathrm{4}} −\mathrm{8}{x}^{\mathrm{3}} +\mathrm{8}{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{3}=\mathrm{0}} ^{{x}+\mathrm{1}=\mathrm{0}\Rightarrow{x}=−\mathrm{1}} \right. \\ $$$${now}\:{we}\:{solve}\::\mathrm{3}{x}^{\mathrm{4}} −\mathrm{8}{x}^{\mathrm{3}} +\mathrm{8}{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{3}=\mathrm{0} \\ $$$$ \\ $$$$ \\ $$
Commented by aleks041103 last updated on 14/Jul/22
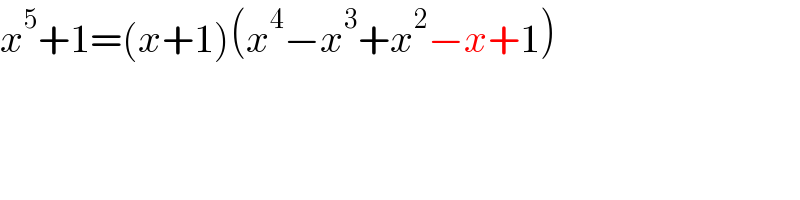
x^5 +1=(x+1)(x^4 −x^3 +x^2 −x+1)
$${x}^{\mathrm{5}} +\mathrm{1}=\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{4}} −{x}^{\mathrm{3}} +{x}^{\mathrm{2}} −{x}+\mathrm{1}\right) \\ $$
Commented by kaivan.ahmadi last updated on 14/Jul/22
thank you
$${thank}\:{you} \\ $$
Commented by mr W last updated on 14/Jul/22
thanks for trying sir!
$${thanks}\:{for}\:{trying}\:{sir}! \\ $$
Answered by CElcedricjunior last updated on 13/Jul/22
{1}
$$\left\{\mathrm{1}\right\} \\ $$
Commented by mr W last updated on 14/Jul/22
wrong. please show how you solved sir.
$${wrong}. \\ $$$${please}\:{show}\:{how}\:{you}\:{solved}\:{sir}. \\ $$
Answered by aleks041103 last updated on 14/Jul/22
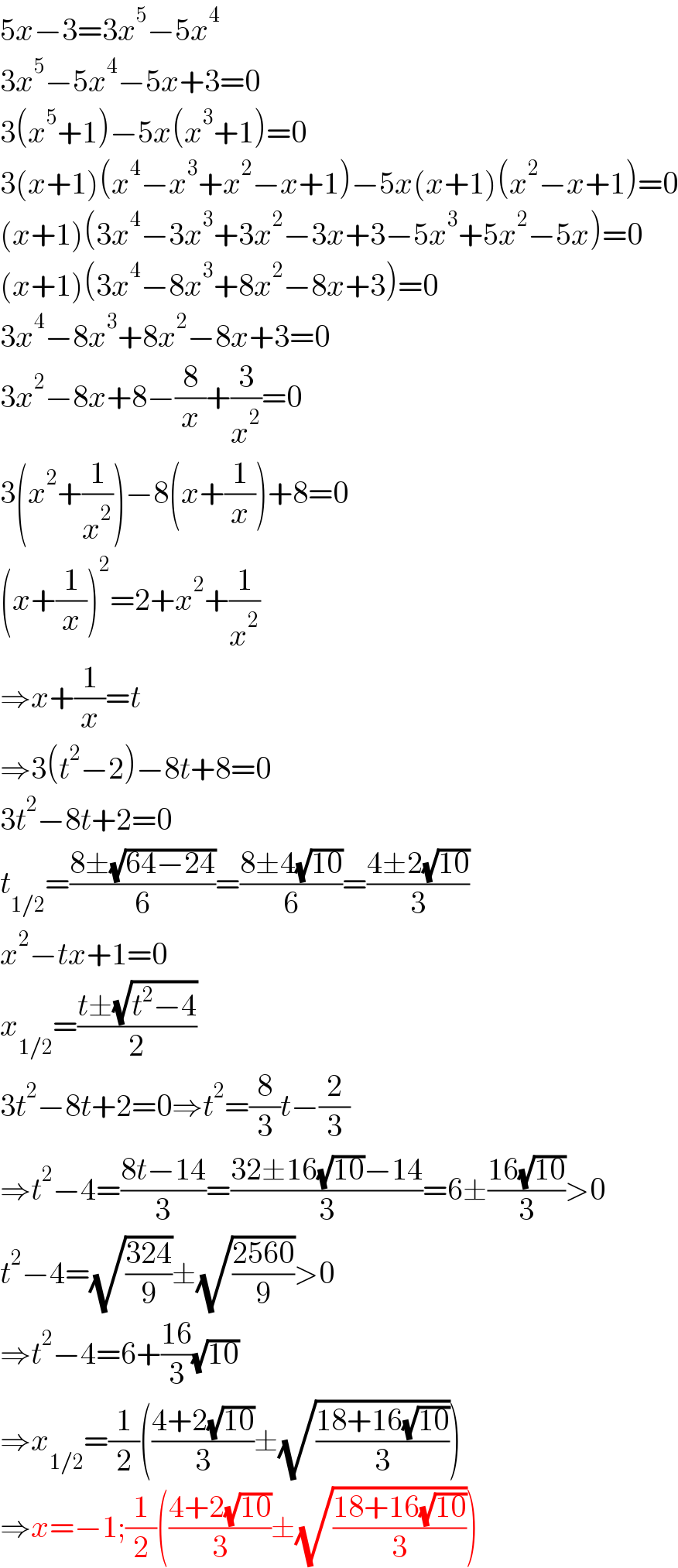
5x−3=3x^5 −5x^4 3x^5 −5x^4 −5x+3=0 3(x^5 +1)−5x(x^3 +1)=0 3(x+1)(x^4 −x^3 +x^2 −x+1)−5x(x+1)(x^2 −x+1)=0 (x+1)(3x^4 −3x^3 +3x^2 −3x+3−5x^3 +5x^2 −5x)=0 (x+1)(3x^4 −8x^3 +8x^2 −8x+3)=0 3x^4 −8x^3 +8x^2 −8x+3=0 3x^2 −8x+8−(8/x)+(3/x^2 )=0 3(x^2 +(1/x^2 ))−8(x+(1/x))+8=0 (x+(1/x))^2 =2+x^2 +(1/x^2 ) ⇒x+(1/x)=t ⇒3(t^2 −2)−8t+8=0 3t^2 −8t+2=0 t_(1/2) =((8±(√(64−24)))/6)=((8±4(√(10)))/6)=((4±2(√(10)))/3) x^2 −tx+1=0 x_(1/2) =((t±(√(t^2 −4)))/2) 3t^2 −8t+2=0⇒t^2 =(8/3)t−(2/3) ⇒t^2 −4=((8t−14)/3)=((32±16(√(10))−14)/3)=6±((16(√(10)))/3)>0 t^2 −4=(√((324)/9))±(√((2560)/9))>0 ⇒t^2 −4=6+((16)/3)(√(10)) ⇒x_(1/2) =(1/2)(((4+2(√(10)))/3)±(√((18+16(√(10)))/3))) ⇒x=−1;(1/2)(((4+2(√(10)))/3)±(√((18+16(√(10)))/3)))
$$\mathrm{5}{x}−\mathrm{3}=\mathrm{3}{x}^{\mathrm{5}} −\mathrm{5}{x}^{\mathrm{4}} \\ $$$$\mathrm{3}{x}^{\mathrm{5}} −\mathrm{5}{x}^{\mathrm{4}} −\mathrm{5}{x}+\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{3}\left({x}^{\mathrm{5}} +\mathrm{1}\right)−\mathrm{5}{x}\left({x}^{\mathrm{3}} +\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{3}\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{4}} −{x}^{\mathrm{3}} +{x}^{\mathrm{2}} −{x}+\mathrm{1}\right)−\mathrm{5}{x}\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left(\mathrm{3}{x}^{\mathrm{4}} −\mathrm{3}{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{3}−\mathrm{5}{x}^{\mathrm{3}} +\mathrm{5}{x}^{\mathrm{2}} −\mathrm{5}{x}\right)=\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left(\mathrm{3}{x}^{\mathrm{4}} −\mathrm{8}{x}^{\mathrm{3}} +\mathrm{8}{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{3}\right)=\mathrm{0} \\ $$$$\mathrm{3}{x}^{\mathrm{4}} −\mathrm{8}{x}^{\mathrm{3}} +\mathrm{8}{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{8}−\frac{\mathrm{8}}{{x}}+\frac{\mathrm{3}}{{x}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\mathrm{3}\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)−\mathrm{8}\left({x}+\frac{\mathrm{1}}{{x}}\right)+\mathrm{8}=\mathrm{0} \\ $$$$\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} =\mathrm{2}+{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$$$\Rightarrow{x}+\frac{\mathrm{1}}{{x}}={t} \\ $$$$\Rightarrow\mathrm{3}\left({t}^{\mathrm{2}} −\mathrm{2}\right)−\mathrm{8}{t}+\mathrm{8}=\mathrm{0} \\ $$$$\mathrm{3}{t}^{\mathrm{2}} −\mathrm{8}{t}+\mathrm{2}=\mathrm{0} \\ $$$${t}_{\mathrm{1}/\mathrm{2}} =\frac{\mathrm{8}\pm\sqrt{\mathrm{64}−\mathrm{24}}}{\mathrm{6}}=\frac{\mathrm{8}\pm\mathrm{4}\sqrt{\mathrm{10}}}{\mathrm{6}}=\frac{\mathrm{4}\pm\mathrm{2}\sqrt{\mathrm{10}}}{\mathrm{3}} \\ $$$${x}^{\mathrm{2}} −{tx}+\mathrm{1}=\mathrm{0} \\ $$$${x}_{\mathrm{1}/\mathrm{2}} =\frac{{t}\pm\sqrt{{t}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}} \\ $$$$\mathrm{3}{t}^{\mathrm{2}} −\mathrm{8}{t}+\mathrm{2}=\mathrm{0}\Rightarrow{t}^{\mathrm{2}} =\frac{\mathrm{8}}{\mathrm{3}}{t}−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\Rightarrow{t}^{\mathrm{2}} −\mathrm{4}=\frac{\mathrm{8}{t}−\mathrm{14}}{\mathrm{3}}=\frac{\mathrm{32}\pm\mathrm{16}\sqrt{\mathrm{10}}−\mathrm{14}}{\mathrm{3}}=\mathrm{6}\pm\frac{\mathrm{16}\sqrt{\mathrm{10}}}{\mathrm{3}}>\mathrm{0} \\ $$$${t}^{\mathrm{2}} −\mathrm{4}=\sqrt{\frac{\mathrm{324}}{\mathrm{9}}}\pm\sqrt{\frac{\mathrm{2560}}{\mathrm{9}}}>\mathrm{0} \\ $$$$\Rightarrow{t}^{\mathrm{2}} −\mathrm{4}=\mathrm{6}+\frac{\mathrm{16}}{\mathrm{3}}\sqrt{\mathrm{10}} \\ $$$$\Rightarrow{x}_{\mathrm{1}/\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{10}}}{\mathrm{3}}\pm\sqrt{\frac{\mathrm{18}+\mathrm{16}\sqrt{\mathrm{10}}}{\mathrm{3}}}\right) \\ $$$$\Rightarrow{x}=−\mathrm{1};\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{10}}}{\mathrm{3}}\pm\sqrt{\frac{\mathrm{18}+\mathrm{16}\sqrt{\mathrm{10}}}{\mathrm{3}}}\right) \\ $$
Commented by mr W last updated on 14/Jul/22
thanks you sir! nice solution!
$${thanks}\:{you}\:{sir}!\:{nice}\:{solution}! \\ $$
Answered by Rasheed.Sindhi last updated on 14/Jul/22
((5x−3)/(3x−5))=x^4 (((5x−3)+(3x−5))/((5x−3)−(3x−5)))=((x^4 +1)/(x^4 −1)) [componendo-_(dividendo...) ((8x−8)/(2x+2))=((x^4 +1)/((x−1)(x+1)(x^2 +1))) ((8(x−1))/(2(x+1)))=((x^4 +1)/((x−1)(x+1)(x^2 +1))) 4(x−1)^2 (x+1)(x^2 +1)−(x+1)(x^4 +1)=0 (x+1){4(x−1)^2 (x^2 +1)−(x^4 +1)}=0 x+1=0 ∣ 3x^4 −8x^3 +8x^2 −8x+3=0 x=−1 ∣ 3(x^2 +(1/x^2 ))−8(x+(1/x))+8=0 x+(1/x)=y⇒x^2 +(1/x^2 )=y^2 −2 3(y^2 −2)−8y+8=0 3y^2 −8y+2=0 For solution of this equation please see sir mr W ′s answer.
$$\frac{\mathrm{5}{x}−\mathrm{3}}{\mathrm{3}{x}−\mathrm{5}}={x}^{\mathrm{4}} \\ $$$$\frac{\left(\mathrm{5}{x}−\mathrm{3}\right)+\left(\mathrm{3}{x}−\mathrm{5}\right)}{\left(\mathrm{5}{x}−\mathrm{3}\right)−\left(\mathrm{3}{x}−\mathrm{5}\right)}=\frac{{x}^{\mathrm{4}} +\mathrm{1}}{{x}^{\mathrm{4}} −\mathrm{1}}\:\left[\underset{{dividendo}…} {{componendo}-}\right. \\ $$$$\frac{\mathrm{8}{x}−\mathrm{8}}{\mathrm{2}{x}+\mathrm{2}}=\frac{{x}^{\mathrm{4}} +\mathrm{1}}{\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$\frac{\mathrm{8}\left({x}−\mathrm{1}\right)}{\mathrm{2}\left({x}+\mathrm{1}\right)}=\frac{{x}^{\mathrm{4}} +\mathrm{1}}{\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$\mathrm{4}\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)−\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{4}} +\mathrm{1}\right)=\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left\{\mathrm{4}\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{1}\right)−\left({x}^{\mathrm{4}} +\mathrm{1}\right)\right\}=\mathrm{0} \\ $$$${x}+\mathrm{1}=\mathrm{0}\:\mid\:\mathrm{3}{x}^{\mathrm{4}} −\mathrm{8}{x}^{\mathrm{3}} +\mathrm{8}{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{3}=\mathrm{0} \\ $$$${x}=−\mathrm{1}\:\mid\:\mathrm{3}\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)−\mathrm{8}\left({x}+\frac{\mathrm{1}}{{x}}\right)+\mathrm{8}=\mathrm{0} \\ $$$${x}+\frac{\mathrm{1}}{{x}}={y}\Rightarrow{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }={y}^{\mathrm{2}} −\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{3}\left({y}^{\mathrm{2}} −\mathrm{2}\right)−\mathrm{8}{y}+\mathrm{8}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{3}{y}^{\mathrm{2}} −\mathrm{8}{y}+\mathrm{2}=\mathrm{0} \\ $$$${For}\:{solution}\:{of}\:{this}\:{equation}\:{please} \\ $$$${see}\:\boldsymbol{{sir}}\:\boldsymbol{{mr}}\:\boldsymbol{{W}}\:'\boldsymbol{{s}}\:{answer}. \\ $$
Answered by mr W last updated on 14/Jul/22
3x^5 +3−5x^4 −5x=0 3(x^5 +1)−5x(x^3 +1)=0 (x+1)[3(x^4 −x^3 +x^2 −x+1)−5x(x^2 −x+1)]=0 (x+1)[3x^4 +3−8x^3 +8x^2 −8x]=0 (x+1)[3(x^2 +(1/x^2 ))−8(x+(1/x))+8]=0 (x+1)[3(x+(1/x))^2 −8(x+(1/x))+2]=0 x+1=0 ⇒x=−1 ✓ 3(x+(1/x))^2 −8(x+(1/x))+2=0 ⇒x+(1/x)=((4+(√(10)))/3) (((4−(√(10)))/3)<2 rejected) x^2 −((4+(√(10)))/3)x+1=0 ⇒x=((4+(√(10))±(√(8(√(10))−10)))/6) ✓
$$\mathrm{3}{x}^{\mathrm{5}} +\mathrm{3}−\mathrm{5}{x}^{\mathrm{4}} −\mathrm{5}{x}=\mathrm{0} \\ $$$$\mathrm{3}\left({x}^{\mathrm{5}} +\mathrm{1}\right)−\mathrm{5}{x}\left({x}^{\mathrm{3}} +\mathrm{1}\right)=\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left[\mathrm{3}\left({x}^{\mathrm{4}} −{x}^{\mathrm{3}} +{x}^{\mathrm{2}} −{x}+\mathrm{1}\right)−\mathrm{5}{x}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)\right]=\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left[\mathrm{3}{x}^{\mathrm{4}} +\mathrm{3}−\mathrm{8}{x}^{\mathrm{3}} +\mathrm{8}{x}^{\mathrm{2}} −\mathrm{8}{x}\right]=\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left[\mathrm{3}\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)−\mathrm{8}\left({x}+\frac{\mathrm{1}}{{x}}\right)+\mathrm{8}\right]=\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left[\mathrm{3}\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{8}\left({x}+\frac{\mathrm{1}}{{x}}\right)+\mathrm{2}\right]=\mathrm{0} \\ $$$${x}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{x}=−\mathrm{1}\:\checkmark \\ $$$$\mathrm{3}\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{8}\left({x}+\frac{\mathrm{1}}{{x}}\right)+\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow{x}+\frac{\mathrm{1}}{{x}}=\frac{\mathrm{4}+\sqrt{\mathrm{10}}}{\mathrm{3}}\:\:\left(\frac{\mathrm{4}−\sqrt{\mathrm{10}}}{\mathrm{3}}<\mathrm{2}\:{rejected}\right) \\ $$$${x}^{\mathrm{2}} −\frac{\mathrm{4}+\sqrt{\mathrm{10}}}{\mathrm{3}}{x}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\mathrm{4}+\sqrt{\mathrm{10}}\pm\sqrt{\mathrm{8}\sqrt{\mathrm{10}}−\mathrm{10}}}{\mathrm{6}}\:\checkmark \\ $$
Answered by Tawa11 last updated on 14/Jul/22
Great sirs
$$\mathrm{Great}\:\mathrm{sirs} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *