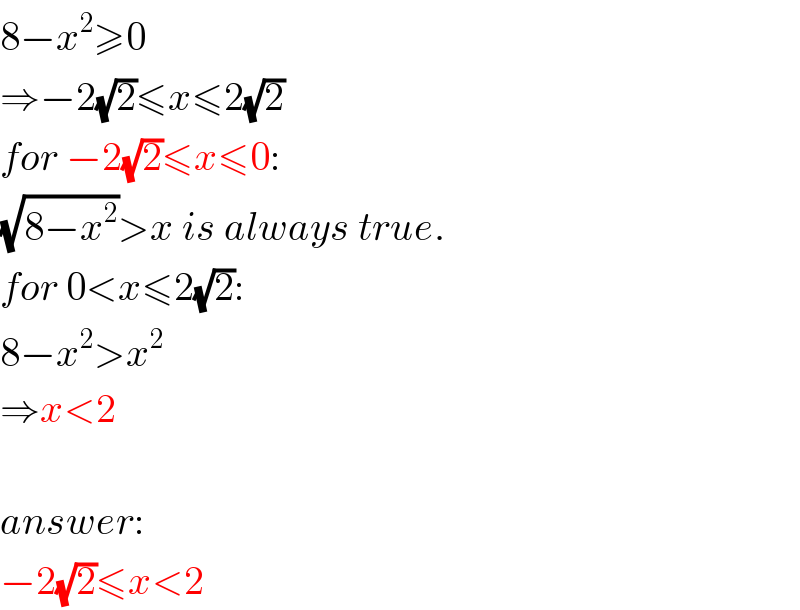Solve-for-x-R-that-suitable-on-this-inequality-8-x-2-gt-x-

Question Number 115312 by naka3546 last updated on 25/Sep/20

S o l v e f o r x \in R t h a t s u i t a b l e o n t h i s

i n e q u a l i t y : \sqrt{8 - x^{2}} > x

Commented by bemath last updated on 25/Sep/20

i n t e r s e c t i o n t w o g r a p h

w e g e t 8 - x^{2} = x^{2} \Rightarrow 8 = 2 x^{2}

x = \pm 2 \Rightarrow s o l u t i o n s e t i s x < 2 .

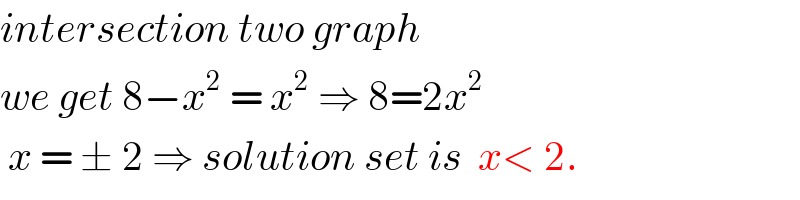
Commented by MJS_new last updated on 25/Sep/20

you are right, two graphs

but f (x) = \sqrt{8 - x^{2}} is defined for - 2 \sqrt{2} ⩽ x ⩽ 2 \sqrt{2}

and f (x) ⩾ 0 . you are not allowed to square

Answered by john santu last updated on 25/Sep/20

(1) 8 - x^{2} ⩾ 0 \Rightarrow (\sqrt{8} + x) (\sqrt{8} - x) ⩾ 0

- 2 \sqrt{2} ⩽ x ⩽ 2 \sqrt{2}

(2) 8 - x^{2} > x^{2} \to 4 - x^{2} > 0

(2 + x) (2 - x) > 0

- 2 < x < 2

s o l u t i o n s e t (1) \cap (2) \Rightarrow - 2 < x < 2

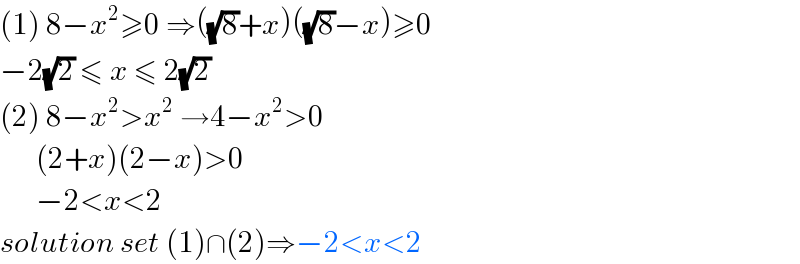
Commented by naka3546 last updated on 25/Sep/20

b u t w h y ? a n y o t h e r s o l u t i o n ?

x = - 2 \sqrt{2} i s r i g h t a n s w e r .

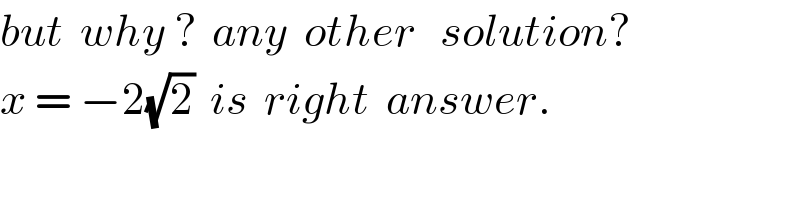
Commented by MJS_new last updated on 25/Sep/20

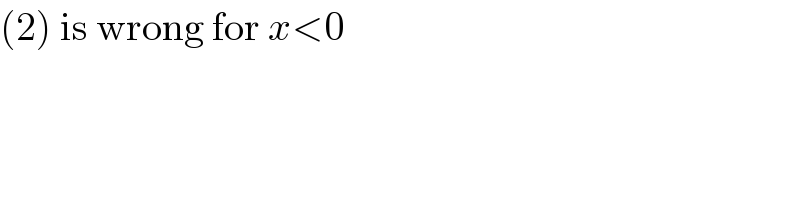
(2) is wrong for x < 0

Answered by MJS_new last updated on 25/Sep/20

\sqrt{8 - x^{2}} > x

\sqrt{8 - x^{2}} defined for - 2 \sqrt{2} ⩽ x ⩽ 2 \sqrt{2}

\sqrt{8 - x^{2}} ⩾ 0 \Rightarrow - 2 \sqrt{2} ⩽ x ⩽ 0 is a part of the

solution

for x > 0 we are allowed to square

8 - x^{2} > x^{2} \land x > 0

\Rightarrow 0 < x < 2

\Rightarrow solution is - 2 \sqrt{2} ⩽ x < 2

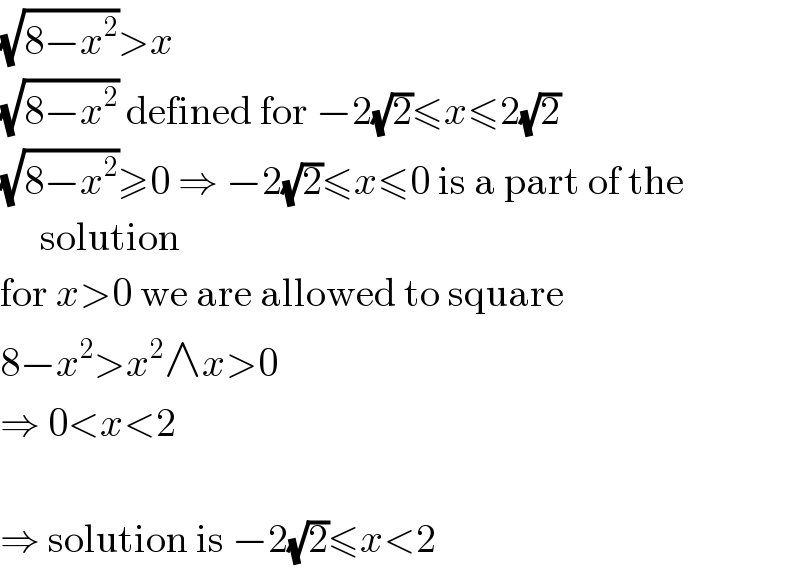
Answered by mr W last updated on 25/Sep/20

8 - x^{2} ⩾ 0

\Rightarrow - 2 \sqrt{2} ⩽ x ⩽ 2 \sqrt{2}

f o r - 2 \sqrt{2} ⩽ x ⩽ 0 :

\sqrt{8 - x^{2}} > x i s a l w a y s t r u e .

f o r 0 < x ⩽ 2 \sqrt{2} :

8 - x^{2} > x^{2}

\Rightarrow x < 2

a n s w e r :

- 2 \sqrt{2} ⩽ x < 2

Facebook Tweet Pin