Question Number 170389 by mr W last updated on 22/May/22
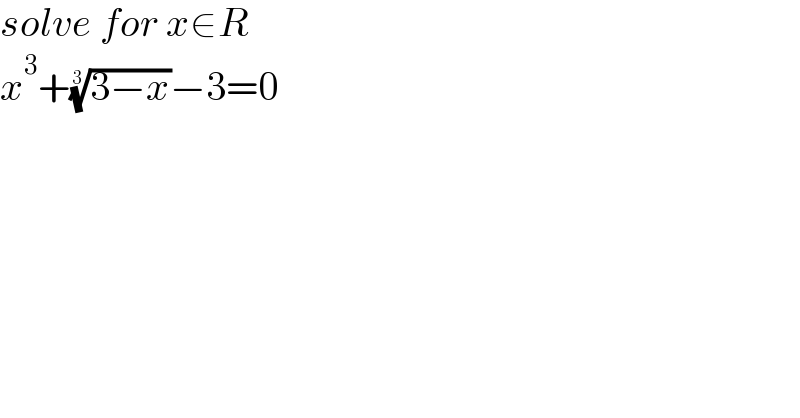
Commented by Mastermind last updated on 22/May/22

Commented by mr W last updated on 22/May/22
Commented by Mastermind last updated on 22/May/22
Commented by jasem1994hamoud last updated on 22/May/22

Commented by mr W last updated on 22/May/22
Commented by Mastermind last updated on 22/May/22
Commented by Mastermind last updated on 22/May/22

Answered by mr W last updated on 22/May/22
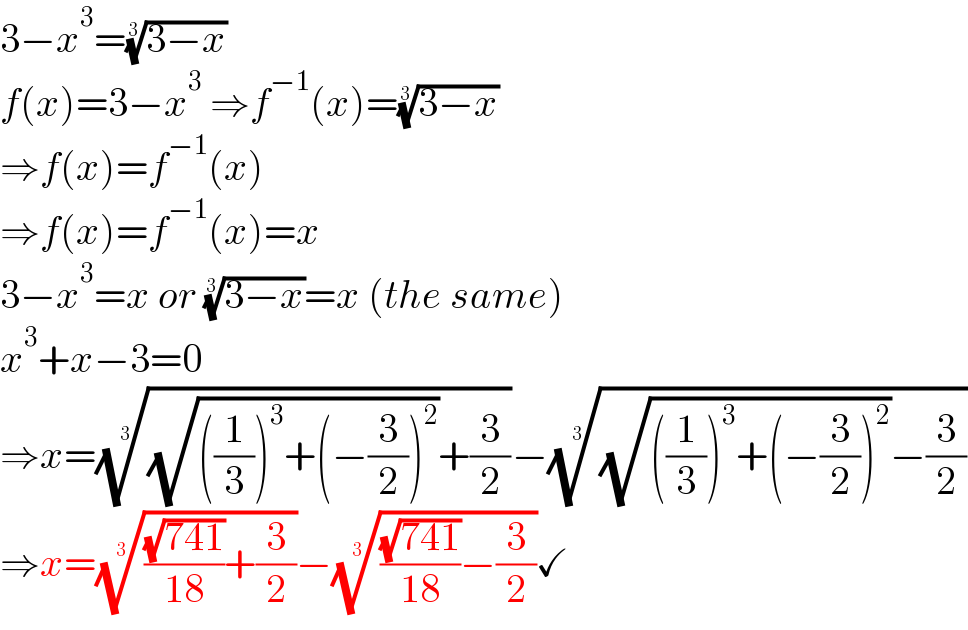
Commented by Mastermind last updated on 22/May/22

Commented by Rasheed.Sindhi last updated on 23/May/22

Commented by MJS_new last updated on 23/May/22

Commented by mr W last updated on 23/May/22

Commented by MJS_new last updated on 23/May/22
![no. I aporoximated all the roots (1) x^3 +((3−x))^(1/3) −3=0 x_1 ≈1.21341166 x_(2, 3) ≈−.597562988±.964934775i these roots don′t give a “nice”polynome: x^3 −.0182856868x^2 −1.56309342 (2) x^3 +x−3=0 x_1 ≈1.21341166 x_(2, 3) ≈−.606705831±1.45061225i (3) [(3−x)^(1/3) =3−x^3 ]^3 ⇒ x^9 −9x^6 +27x^3 −x−24=0 (x^3 +x−3)(x^6 −x^4 −6x^3 +x^2 +3x+8)=0 x^6 −4^4 +6x^3 +x^2 +3x+8=0 x_(1, 2) ≈1.54420759±.135231222i x_(3, 4) ≈−.597562988±.964934775i x_(5, 6) ≈−.946644598±1.29938754i](https://www.tinkutara.com/question/Q170429.png)
Commented by mr W last updated on 23/May/22

Commented by Tawa11 last updated on 08/Oct/22

