Question Number 169653 by infinityaction last updated on 05/May/22
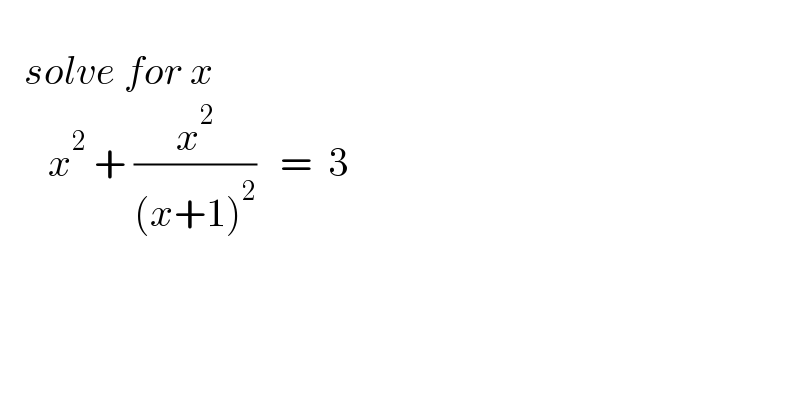
$$ \\ $$$$\:\:\:{solve}\:{for}\:{x} \\ $$$$\:\:\:\:\:\:{x}^{\mathrm{2}} \:+\:\frac{{x}^{\mathrm{2}} }{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }\:\:\:=\:\:\mathrm{3} \\ $$
Answered by mr W last updated on 05/May/22
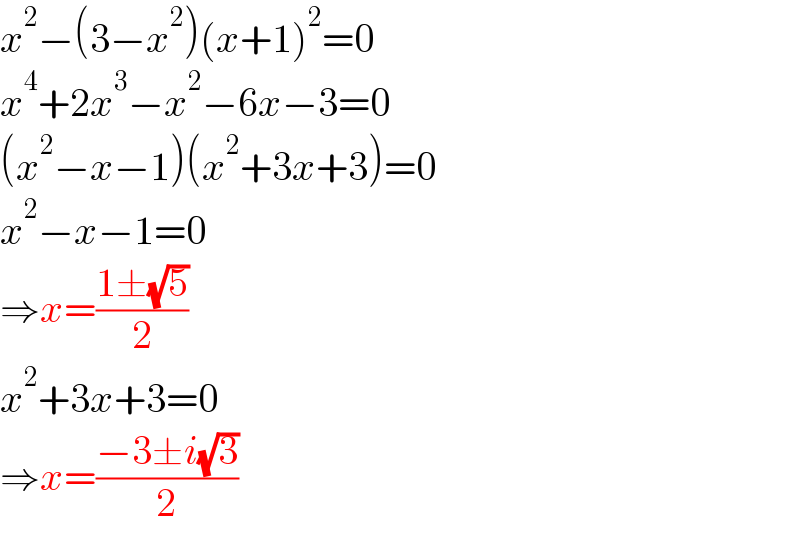
$${x}^{\mathrm{2}} −\left(\mathrm{3}−{x}^{\mathrm{2}} \right)\left({x}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} −{x}^{\mathrm{2}} −\mathrm{6}{x}−\mathrm{3}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} −{x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{3}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −{x}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{3}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{−\mathrm{3}\pm{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$
Commented by infinityaction last updated on 05/May/22

$${thank}\:{you}\:{sir} \\ $$
