solve-for-x-x-4-4x-1-0-

Question Number 45896 by Sanjarbek last updated on 18/Oct/18

s o l v e f o r x

x^{4} - 4 x + 1 = 0

Commented by tanmay.chaudhury50@gmail.com last updated on 18/Oct/18

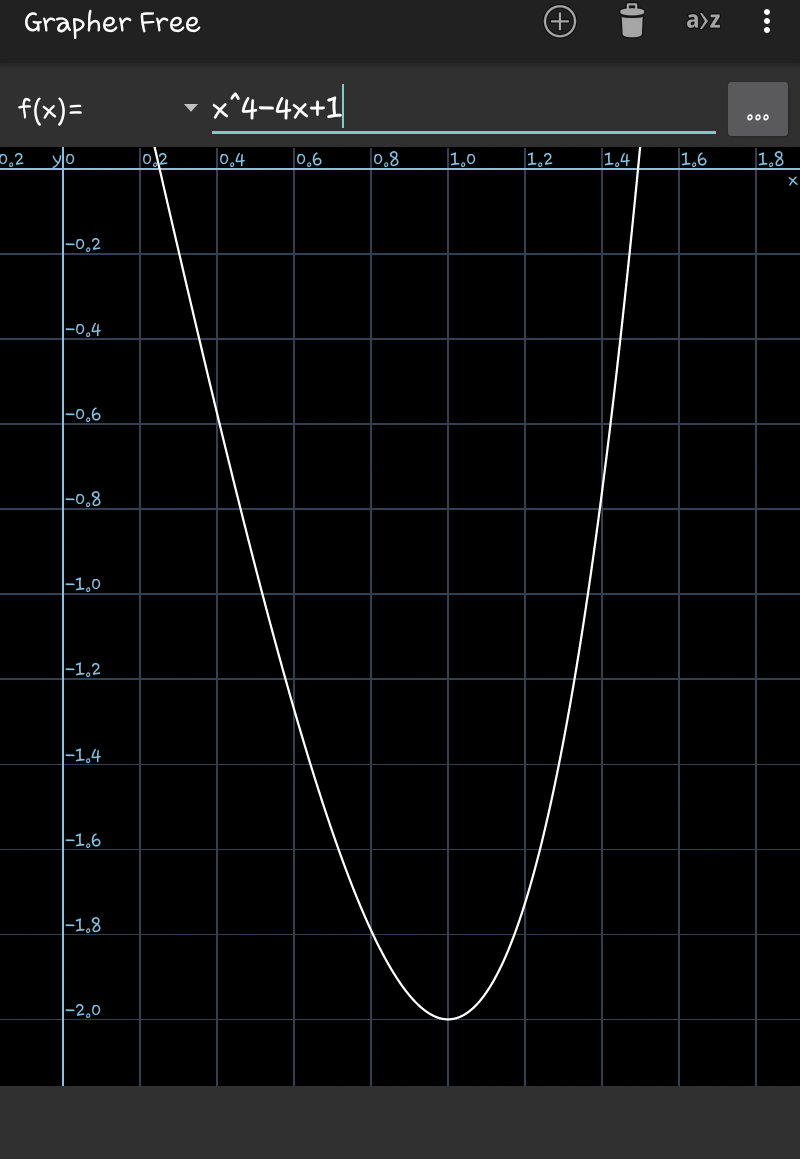
Commented by tanmay.chaudhury50@gmail.com last updated on 18/Oct/18

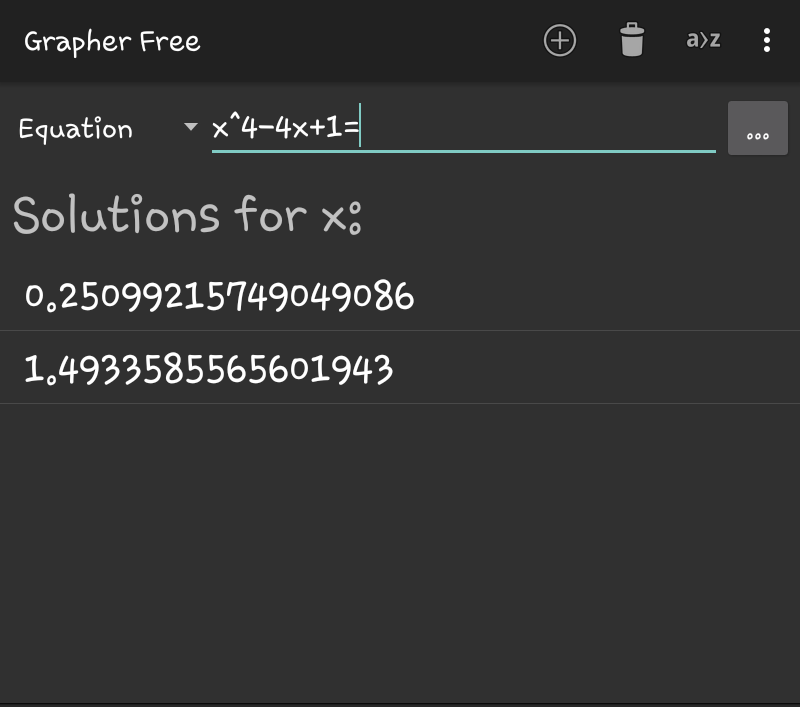
Answered by ajfour last updated on 19/Oct/18

l e t x^{4} - 4 x + 1 = 0

\Leftrightarrow (x^{2} + a x + b) (x^{2} - a x + \frac{1}{b}) = 0

\Leftrightarrow x^{4} + (b + \frac{1}{b} - a^{2}) x^{2} + a (\frac{1}{b} - b) x + 1 = 0

\Rightarrow \frac{1}{b} + b = a^{2}; \frac{1}{b} - b = - \frac{4}{a}

a d d i n g : a^{2} - \frac{4}{a} = \frac{2}{b} \dots (i)

s u b t r a c t i n g : a^{2} + \frac{4}{a} = 2 b \dots (i i)

\Rightarrow b > 0

m u l t i p l y i n g a b o v e t w o e q s .

a^{4} - \frac{16}{a^{2}} = 4

l e t s = a^{2}, t h e n

s^{3} - 4 s - 16 = 0

\Rightarrow s = a^{2} = {(8 + \frac{8}{3} \sqrt{\frac{26}{3}})}^{1 / 3} + {(8 - \frac{8}{3} \sqrt{\frac{26}{3}})}^{1 / 3}

a^{2} \approx 3.04275941

a \approx \pm 1.74435071

b = \frac{a^{2}}{2} + \frac{2}{a}

w i t h + v e a, b_{1} \approx 2.66793813

w i t h - v e a, b_{2} \approx 0.374821282

b o t h s e t s s a t i s f y e q s . (i) & (i i)

F o r + v e a & b_{1}

x^{2} + a x + b = 0 p r o v i d e s

x = - \frac{a}{2} \pm \sqrt{\frac{a^{2}}{4} - b}

n o r e a l r o o t s; w h i l e

x^{2} - a x + 1 / b = 0 g i v e s

x \approx - 1.49336, - 0.25099

F o r - v e a & b_{2}

x^{2} + a x + b = 0 g i v e s

x \approx 0.25099, 1.49336

w h i l e x^{2} - a x + 1 / b = 0 g i v e s

n o r e a l r o o t s .

B u t \frac{d}{d x} (x^{4} - 4 x + 1) = 4 x^{3} - 4

\Rightarrow \frac{d y}{d x} = 0 o n l y a t x = 1

s o o n e r o o t i s c e r t a i n l y > 1

\Rightarrow w e n e e d t o r e j e c t t h e n e g a t i v e

s e t o f r o o t s; t h e a n s w e r i s i n d e e d

x_{1} \approx 0.25099 & x_{2} \approx 1.49336 .

Commented by peter frank last updated on 18/Oct/18

second line sir clarify plz

Commented by ajfour last updated on 18/Oct/18

c o e f f . o f x^{3} i s 0 a n d c o n s t a n t

t e r m i s 1, a n d i a s s u m e d a d e g r e e 4

e x p r e s s i o n a s a p r o d u c t o f t w o

q u a d r a t i c e x p r e s s i o n s . .

Commented by peter frank last updated on 20/Oct/18

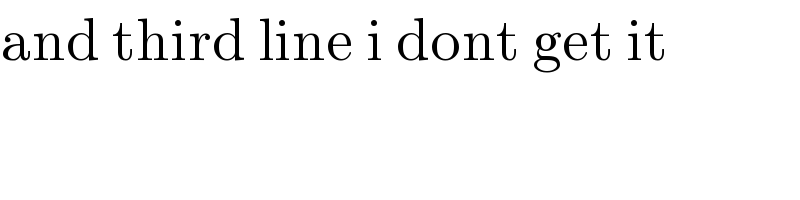
and third line i dont get it

Commented by ajfour last updated on 20/Oct/18

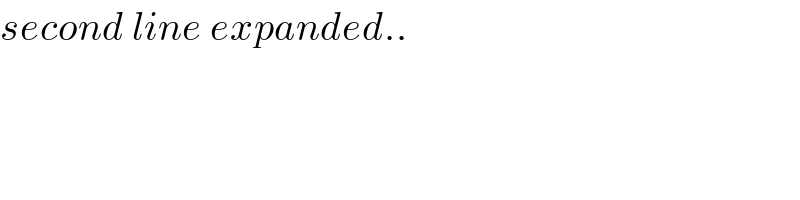
s e c o n d l i n e e x p a n d e d . .

Commented by peter frank last updated on 20/Oct/18

thanks

Answered by mondodotto@gmail.com last updated on 18/Oct/18