Question Number 124880 by WilliamsErinfolami last updated on 06/Dec/20
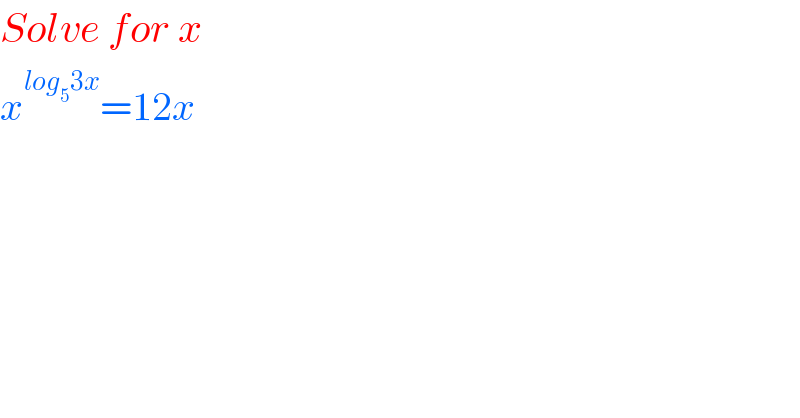
$${Solve}\:{for}\:{x} \\ $$$${x}^{{log}_{\mathrm{5}} \mathrm{3}{x}} =\mathrm{12}{x} \\ $$
Answered by mr W last updated on 06/Dec/20
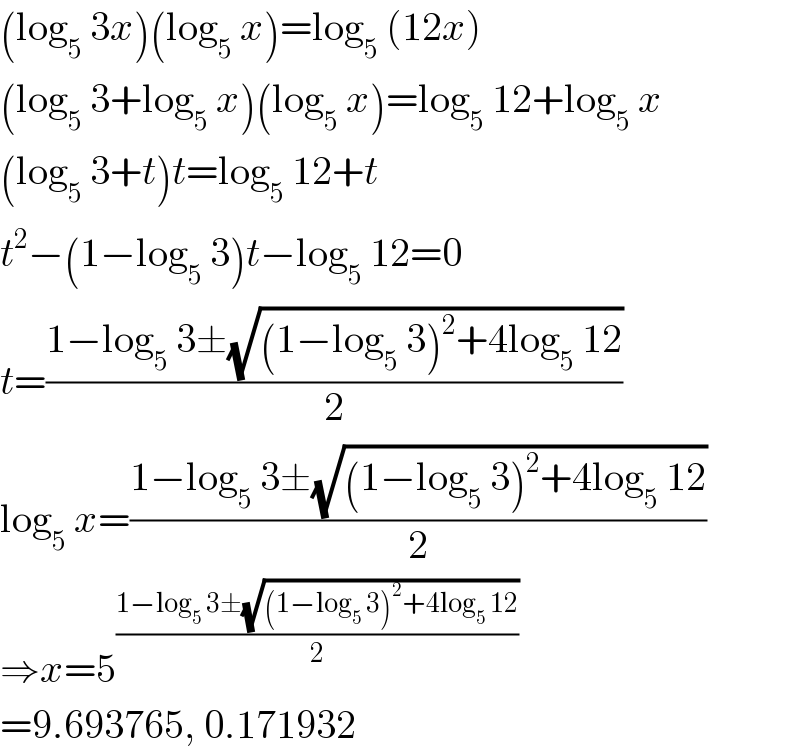
$$\left(\mathrm{log}_{\mathrm{5}} \:\mathrm{3}{x}\right)\left(\mathrm{log}_{\mathrm{5}} \:{x}\right)=\mathrm{log}_{\mathrm{5}} \:\left(\mathrm{12}{x}\right) \\ $$$$\left(\mathrm{log}_{\mathrm{5}} \:\mathrm{3}+\mathrm{log}_{\mathrm{5}} \:{x}\right)\left(\mathrm{log}_{\mathrm{5}} \:{x}\right)=\mathrm{log}_{\mathrm{5}} \:\mathrm{12}+\mathrm{log}_{\mathrm{5}} \:{x} \\ $$$$\left(\mathrm{log}_{\mathrm{5}} \:\mathrm{3}+{t}\right){t}=\mathrm{log}_{\mathrm{5}} \:\mathrm{12}+{t} \\ $$$${t}^{\mathrm{2}} −\left(\mathrm{1}−\mathrm{log}_{\mathrm{5}} \:\mathrm{3}\right){t}−\mathrm{log}_{\mathrm{5}} \:\mathrm{12}=\mathrm{0} \\ $$$${t}=\frac{\mathrm{1}−\mathrm{log}_{\mathrm{5}} \:\mathrm{3}\pm\sqrt{\left(\mathrm{1}−\mathrm{log}_{\mathrm{5}} \:\mathrm{3}\right)^{\mathrm{2}} +\mathrm{4log}_{\mathrm{5}} \:\mathrm{12}}}{\mathrm{2}} \\ $$$$\mathrm{log}_{\mathrm{5}} \:{x}=\frac{\mathrm{1}−\mathrm{log}_{\mathrm{5}} \:\mathrm{3}\pm\sqrt{\left(\mathrm{1}−\mathrm{log}_{\mathrm{5}} \:\mathrm{3}\right)^{\mathrm{2}} +\mathrm{4log}_{\mathrm{5}} \:\mathrm{12}}}{\mathrm{2}} \\ $$$$\Rightarrow{x}=\mathrm{5}^{\frac{\mathrm{1}−\mathrm{log}_{\mathrm{5}} \:\mathrm{3}\pm\sqrt{\left(\mathrm{1}−\mathrm{log}_{\mathrm{5}} \:\mathrm{3}\right)^{\mathrm{2}} +\mathrm{4log}_{\mathrm{5}} \:\mathrm{12}}}{\mathrm{2}}} \\ $$$$=\mathrm{9}.\mathrm{693765},\:\mathrm{0}.\mathrm{171932} \\ $$
Answered by aleks041103 last updated on 06/Dec/20
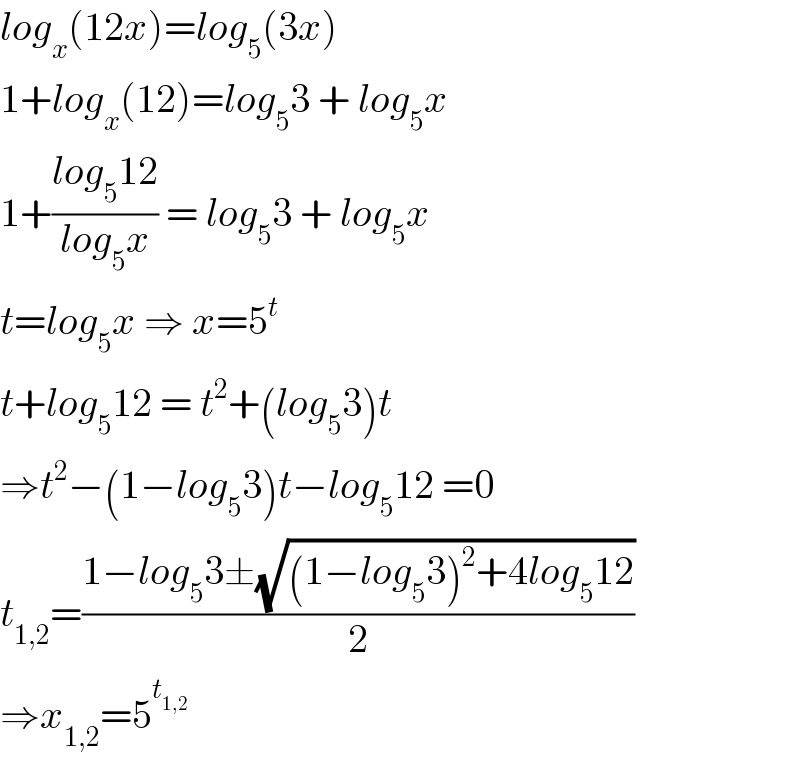
$${log}_{{x}} \left(\mathrm{12}{x}\right)={log}_{\mathrm{5}} \left(\mathrm{3}{x}\right) \\ $$$$\mathrm{1}+{log}_{{x}} \left(\mathrm{12}\right)={log}_{\mathrm{5}} \mathrm{3}\:+\:{log}_{\mathrm{5}} {x} \\ $$$$\mathrm{1}+\frac{{log}_{\mathrm{5}} \mathrm{12}}{{log}_{\mathrm{5}} {x}}\:=\:{log}_{\mathrm{5}} \mathrm{3}\:+\:{log}_{\mathrm{5}} {x} \\ $$$${t}={log}_{\mathrm{5}} {x}\:\Rightarrow\:{x}=\mathrm{5}^{{t}} \\ $$$${t}+{log}_{\mathrm{5}} \mathrm{12}\:=\:{t}^{\mathrm{2}} +\left({log}_{\mathrm{5}} \mathrm{3}\right){t} \\ $$$$\Rightarrow{t}^{\mathrm{2}} −\left(\mathrm{1}−{log}_{\mathrm{5}} \mathrm{3}\right){t}−{log}_{\mathrm{5}} \mathrm{12}\:=\mathrm{0} \\ $$$${t}_{\mathrm{1},\mathrm{2}} =\frac{\mathrm{1}−{log}_{\mathrm{5}} \mathrm{3}\pm\sqrt{\left(\mathrm{1}−{log}_{\mathrm{5}} \mathrm{3}\right)^{\mathrm{2}} +\mathrm{4}{log}_{\mathrm{5}} \mathrm{12}}}{\mathrm{2}} \\ $$$$\Rightarrow{x}_{\mathrm{1},\mathrm{2}} =\mathrm{5}^{{t}_{\mathrm{1},\mathrm{2}} } \\ $$
