Question Number 175402 by Linton last updated on 29/Aug/22
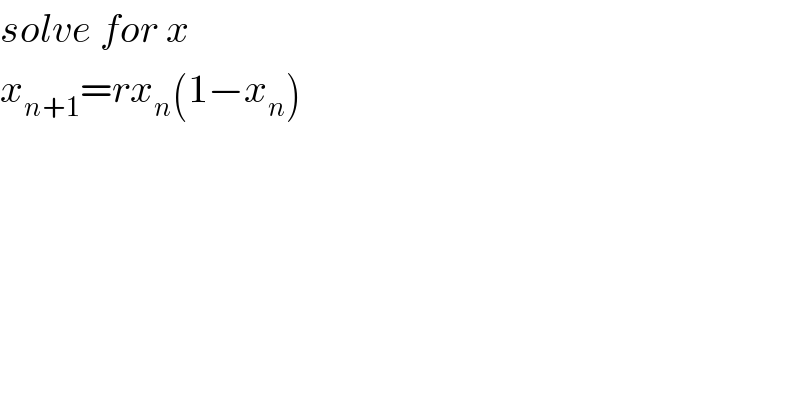
$${solve}\:{for}\:{x} \\ $$$${x}_{{n}+\mathrm{1}} ={rx}_{{n}} \left(\mathrm{1}−{x}_{{n}} \right) \\ $$
Commented by a.lgnaoui last updated on 31/Aug/22
![x_1 =rx_0 (1−x_0 ) x_2 =rx_1 (1−x_1 ) x_3 =rx_2 (1−x_2 ) ....... x_(n+1) =rx_n (1−x_n ) −−−−−−−− Π _(i=1)^n (x_i )=r^n Πx_i (1−x_i )=x_1 .x_2 .x_3 ......x_n 1=r^n x_0 (1−x_n ) x_n =1−(1/(x_0 r^n )) (1) x_1 =rx_0 (1−x_0 ) x_2 =rx_1 (1−x_1 )=r[rx_0 (1−x_0 )][1−rx_0 (1−x_0 )] =r^2 x_0 (1−x_0 )−r^3 x_0 ^2 (1−x_0 )^2 x_3 =rx_2 (1−x_2 )=[r(rx_1 (1−x_1 ))][1−rx_1 (1−x_1 )] =r^2 x_1 (1−x_1 )−r^3 x_1 ^2 (1−x_1 )^2 x_4 =r^2 x_2 (1−x_2 )−r^3 x_2 ^2 (1−x_2 )^2 ........ x_n =r^2 x_(n−2) (1−x_(n−2) )−r^3 (1−x_(n−2) )^2 Σx_i =r[(r(x_0 (1−x_0 )+rx_1 (1−x_1 )+rx_2 (1−x_2 )+.....rx_(n−2) (1−x_(n−2) )−r×[r^2 [x_0 (1−x_0 )^2 +x_1 ^2 (1−x_1 )^2 +x_3 ^2 (1−x_3 )^2 +.....x_(n−2) ^2 (1−x_(n−2) )^2 Σx_i =r[x_1 +x_2 +x_3 +....x_(n−1) ]+r[x_1 ^2 +x_2 ^2 +x_3 ^2 +...x_(n−1) ^2 ] ? (1−r)Σx_i =r(Σx_i ^2 ) Σx_i =((rΣx_i ^2 )/(1−r)) ? .............](https://www.tinkutara.com/question/Q175497.png)
$${x}_{\mathrm{1}} ={rx}_{\mathrm{0}} \left(\mathrm{1}−{x}_{\mathrm{0}} \right) \\ $$$${x}_{\mathrm{2}} ={rx}_{\mathrm{1}} \left(\mathrm{1}−{x}_{\mathrm{1}} \right) \\ $$$${x}_{\mathrm{3}} ={rx}_{\mathrm{2}} \left(\mathrm{1}−{x}_{\mathrm{2}} \right) \\ $$$$……. \\ $$$${x}_{{n}+\mathrm{1}} ={rx}_{{n}} \left(\mathrm{1}−{x}_{{n}} \right) \\ $$$$−−−−−−−− \\ $$$$\Pi\:_{{i}=\mathrm{1}} ^{{n}} \left({x}_{{i}} \right)={r}^{{n}} \Pi{x}_{{i}} \left(\mathrm{1}−{x}_{{i}} \right)={x}_{\mathrm{1}} .{x}_{\mathrm{2}} .{x}_{\mathrm{3}} ……{x}_{{n}} \\ $$$$\mathrm{1}={r}^{{n}} {x}_{\mathrm{0}} \left(\mathrm{1}−{x}_{{n}} \right) \\ $$$${x}_{{n}} =\mathrm{1}−\frac{\mathrm{1}}{{x}_{\mathrm{0}} {r}^{{n}} }\:\:\:\left(\mathrm{1}\right) \\ $$$$ \\ $$$${x}_{\mathrm{1}} ={rx}_{\mathrm{0}} \left(\mathrm{1}−{x}_{\mathrm{0}} \right) \\ $$$${x}_{\mathrm{2}} ={rx}_{\mathrm{1}} \left(\mathrm{1}−{x}_{\mathrm{1}} \right)={r}\left[{rx}_{\mathrm{0}} \left(\mathrm{1}−{x}_{\mathrm{0}} \right)\right]\left[\mathrm{1}−{rx}_{\mathrm{0}} \left(\mathrm{1}−{x}_{\mathrm{0}} \right)\right] \\ $$$$={r}^{\mathrm{2}} {x}_{\mathrm{0}} \left(\mathrm{1}−{x}_{\mathrm{0}} \right)−{r}^{\mathrm{3}} {x}_{\mathrm{0}} ^{\mathrm{2}} \left(\mathrm{1}−{x}_{\mathrm{0}} \right)^{\mathrm{2}} \\ $$$${x}_{\mathrm{3}} ={rx}_{\mathrm{2}} \left(\mathrm{1}−{x}_{\mathrm{2}} \right)=\left[{r}\left({rx}_{\mathrm{1}} \left(\mathrm{1}−{x}_{\mathrm{1}} \right)\right)\right]\left[\mathrm{1}−{rx}_{\mathrm{1}} \left(\mathrm{1}−{x}_{\mathrm{1}} \right)\right] \\ $$$$={r}^{\mathrm{2}} {x}_{\mathrm{1}} \left(\mathrm{1}−{x}_{\mathrm{1}} \right)−{r}^{\mathrm{3}} {x}_{\mathrm{1}} ^{\mathrm{2}} \left(\mathrm{1}−{x}_{\mathrm{1}} \right)^{\mathrm{2}} \\ $$$${x}_{\mathrm{4}} ={r}^{\mathrm{2}} {x}_{\mathrm{2}} \left(\mathrm{1}−{x}_{\mathrm{2}} \right)−{r}^{\mathrm{3}} {x}_{\mathrm{2}} ^{\mathrm{2}} \left(\mathrm{1}−{x}_{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$…….. \\ $$$${x}_{{n}} ={r}^{\mathrm{2}} {x}_{{n}−\mathrm{2}} \left(\mathrm{1}−{x}_{{n}−\mathrm{2}} \right)−{r}^{\mathrm{3}} \left(\mathrm{1}−{x}_{{n}−\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\Sigma{x}_{{i}} ={r}\left[\left({r}\left({x}_{\mathrm{0}} \left(\mathrm{1}−{x}_{\mathrm{0}} \right)+{rx}_{\mathrm{1}} \left(\mathrm{1}−{x}_{\mathrm{1}} \right)+{rx}_{\mathrm{2}} \left(\mathrm{1}−{x}_{\mathrm{2}} \right)+…..{rx}_{{n}−\mathrm{2}} \left(\mathrm{1}−{x}_{{n}−\mathrm{2}} \right)−{r}×\left[{r}^{\mathrm{2}} \left[{x}_{\mathrm{0}} \left(\mathrm{1}−{x}_{\mathrm{0}} \right)^{\mathrm{2}} +{x}_{\mathrm{1}} ^{\mathrm{2}} \left(\mathrm{1}−{x}_{\mathrm{1}} \right)^{\mathrm{2}} +{x}_{\mathrm{3}} ^{\mathrm{2}} \left(\mathrm{1}−{x}_{\mathrm{3}} \right)^{\mathrm{2}} +…..{x}_{{n}−\mathrm{2}} ^{\mathrm{2}} \left(\mathrm{1}−{x}_{{n}−\mathrm{2}} \right)^{\mathrm{2}} \right.\right.\right.\right.\right. \\ $$$$\Sigma{x}_{{i}} ={r}\left[{x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} +….{x}_{{n}−\mathrm{1}} \right]+{r}\left[{x}_{\mathrm{1}} ^{\mathrm{2}} +{x}_{\mathrm{2}} ^{\mathrm{2}} +{x}_{\mathrm{3}} ^{\mathrm{2}} +…{x}_{{n}−\mathrm{1}} ^{\mathrm{2}} \right]\:\:\:? \\ $$$$\left(\mathrm{1}−{r}\right)\Sigma{x}_{{i}} ={r}\left(\Sigma{x}_{{i}} ^{\mathrm{2}} \right) \\ $$$$\Sigma{x}_{{i}} =\frac{{r}\Sigma{x}_{{i}} ^{\mathrm{2}} }{\mathrm{1}−{r}}\:\:\:\:? \\ $$$$…………. \\ $$
