Question Number 171821 by Mikenice last updated on 21/Jun/22
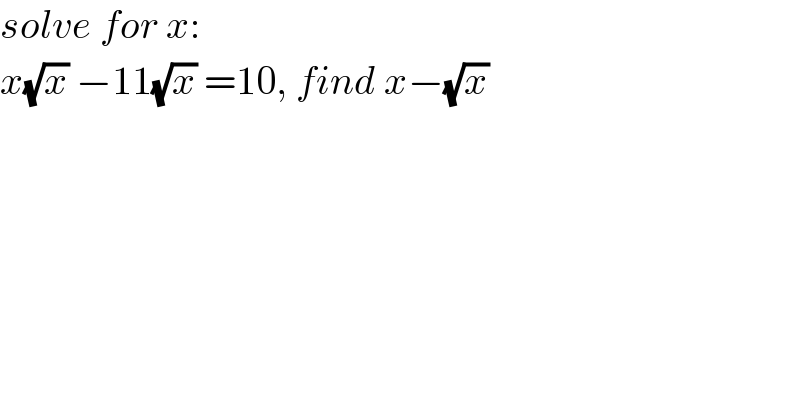
$${solve}\:{for}\:{x}: \\ $$$${x}\sqrt{{x}}\:−\mathrm{11}\sqrt{{x}}\:=\mathrm{10},\:{find}\:{x}−\sqrt{{x}} \\ $$
Commented by mr W last updated on 21/Jun/22
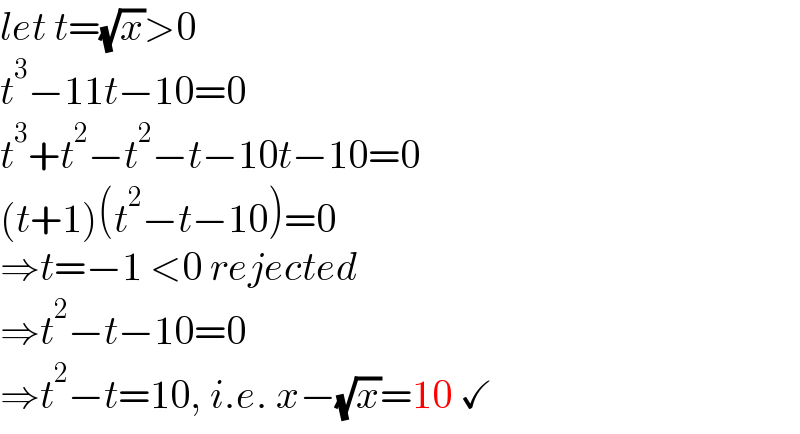
$${let}\:{t}=\sqrt{{x}}>\mathrm{0} \\ $$$${t}^{\mathrm{3}} −\mathrm{11}{t}−\mathrm{10}=\mathrm{0} \\ $$$${t}^{\mathrm{3}} +{t}^{\mathrm{2}} −{t}^{\mathrm{2}} −{t}−\mathrm{10}{t}−\mathrm{10}=\mathrm{0} \\ $$$$\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} −{t}−\mathrm{10}\right)=\mathrm{0} \\ $$$$\Rightarrow{t}=−\mathrm{1}\:<\mathrm{0}\:{rejected} \\ $$$$\Rightarrow{t}^{\mathrm{2}} −{t}−\mathrm{10}=\mathrm{0} \\ $$$$\Rightarrow{t}^{\mathrm{2}} −{t}=\mathrm{10},\:{i}.{e}.\:{x}−\sqrt{{x}}=\mathrm{10}\:\checkmark \\ $$
