Question Number 79571 by TawaTawa last updated on 26/Jan/20
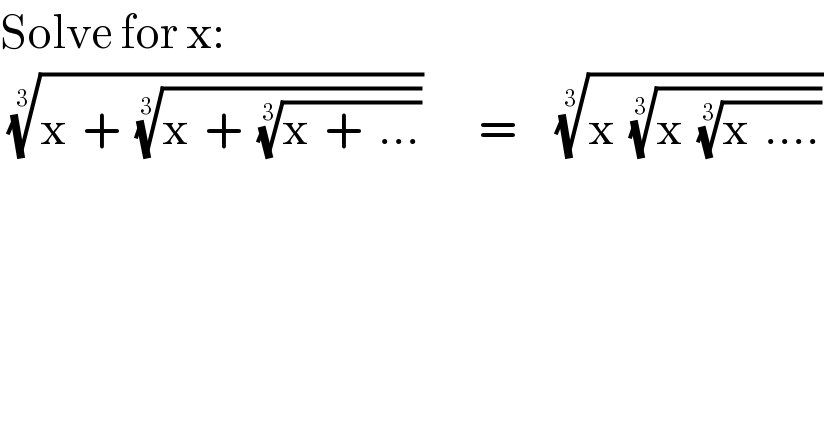
$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{x}: \\ $$$$\:\sqrt[{\mathrm{3}}]{\mathrm{x}\:\:+\:\:\sqrt[{\mathrm{3}}]{\mathrm{x}\:\:+\:\:\sqrt[{\mathrm{3}}]{\mathrm{x}\:\:+\:\:…}}}\:\:\:\:\:\:\:=\:\:\:\:\:\sqrt[{\mathrm{3}}]{\mathrm{x}\:\:\sqrt[{\mathrm{3}}]{\mathrm{x}\:\:\sqrt[{\mathrm{3}}]{\mathrm{x}\:\:….}}} \\ $$
Commented by MJS last updated on 26/Jan/20
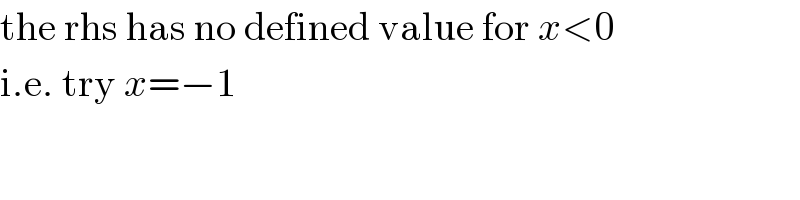
$$\mathrm{the}\:\mathrm{rhs}\:\mathrm{has}\:\mathrm{no}\:\mathrm{defined}\:\mathrm{value}\:\mathrm{for}\:{x}<\mathrm{0} \\ $$$$\mathrm{i}.\mathrm{e}.\:\mathrm{try}\:{x}=−\mathrm{1} \\ $$
Commented by MJS last updated on 26/Jan/20
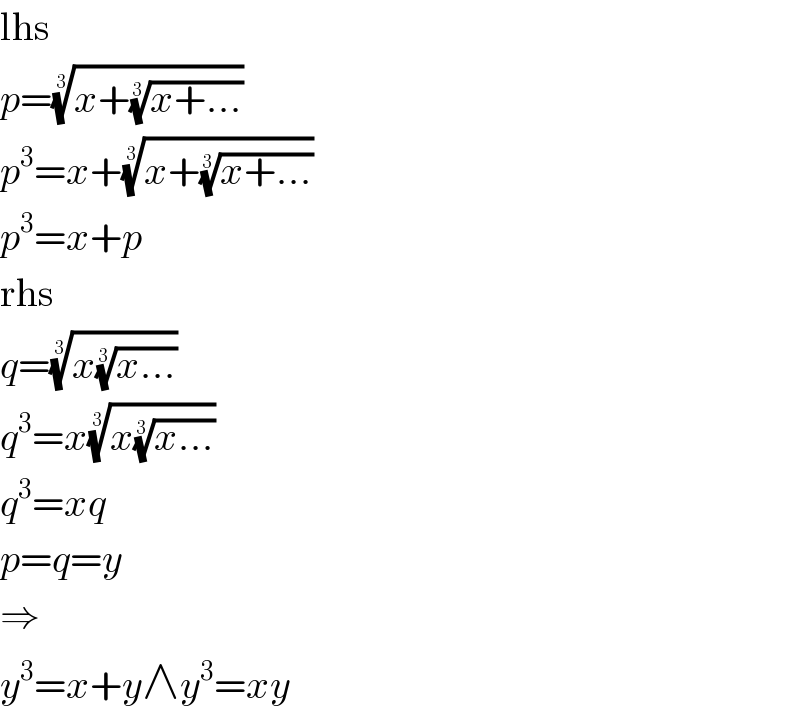
$$\mathrm{lhs} \\ $$$${p}=\sqrt[{\mathrm{3}}]{{x}+\sqrt[{\mathrm{3}}]{{x}+…}} \\ $$$${p}^{\mathrm{3}} ={x}+\sqrt[{\mathrm{3}}]{{x}+\sqrt[{\mathrm{3}}]{{x}+…}} \\ $$$${p}^{\mathrm{3}} ={x}+{p} \\ $$$$\mathrm{rhs} \\ $$$${q}=\sqrt[{\mathrm{3}}]{{x}\sqrt[{\mathrm{3}}]{{x}…}} \\ $$$${q}^{\mathrm{3}} ={x}\sqrt[{\mathrm{3}}]{{x}\sqrt[{\mathrm{3}}]{{x}…}} \\ $$$${q}^{\mathrm{3}} ={xq} \\ $$$${p}={q}={y} \\ $$$$\Rightarrow \\ $$$${y}^{\mathrm{3}} ={x}+{y}\wedge{y}^{\mathrm{3}} ={xy} \\ $$
Commented by john santu last updated on 26/Jan/20
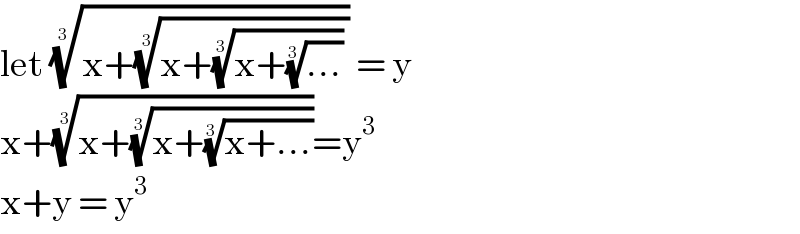
$$\mathrm{let}\:\sqrt[{\mathrm{3}\:}]{\mathrm{x}+\sqrt[{\mathrm{3}}]{\mathrm{x}+\sqrt[{\mathrm{3}}]{\mathrm{x}+\sqrt[{\mathrm{3}}]{…}}\:}}\:=\:\mathrm{y}\: \\ $$$$\mathrm{x}+\sqrt[{\mathrm{3}}]{\mathrm{x}+\sqrt[{\mathrm{3}}]{\mathrm{x}+\sqrt[{\mathrm{3}}]{\mathrm{x}+…}}}=\mathrm{y}^{\mathrm{3}} \\ $$$$\mathrm{x}+\mathrm{y}\:=\:\mathrm{y}^{\mathrm{3}} \: \\ $$
Commented by john santu last updated on 26/Jan/20

$$\mathrm{haha}\:\mathrm{i}\:\mathrm{didn}'\mathrm{t}\:\mathrm{see}\:\mathrm{the}\:\mathrm{right}\:\mathrm{section} \\ $$$$\mathrm{because}\:\mathrm{it}\:\mathrm{was}\:\mathrm{written}\:\mathrm{in}\:\mathrm{1}\:\mathrm{line} \\ $$
Commented by TawaTawa last updated on 26/Jan/20

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir},\:\:\mathrm{i}\:\mathrm{understand}\:\mathrm{now} \\ $$
Answered by MJS last updated on 26/Jan/20
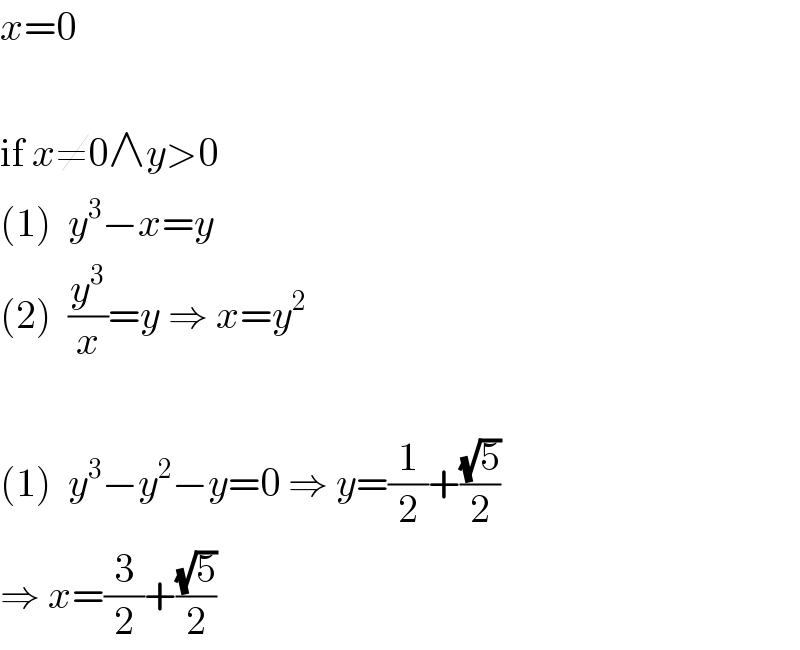
$${x}=\mathrm{0} \\ $$$$ \\ $$$$\mathrm{if}\:{x}\neq\mathrm{0}\wedge{y}>\mathrm{0} \\ $$$$\left(\mathrm{1}\right)\:\:{y}^{\mathrm{3}} −{x}={y} \\ $$$$\left(\mathrm{2}\right)\:\:\frac{{y}^{\mathrm{3}} }{{x}}={y}\:\Rightarrow\:{x}={y}^{\mathrm{2}} \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:\:{y}^{\mathrm{3}} −{y}^{\mathrm{2}} −{y}=\mathrm{0}\:\Rightarrow\:{y}=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\Rightarrow\:{x}=\frac{\mathrm{3}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$
Commented by john santu last updated on 26/Jan/20

$$\mathrm{cardano}\:\mathrm{againt} \\ $$
Commented by MJS last updated on 26/Jan/20
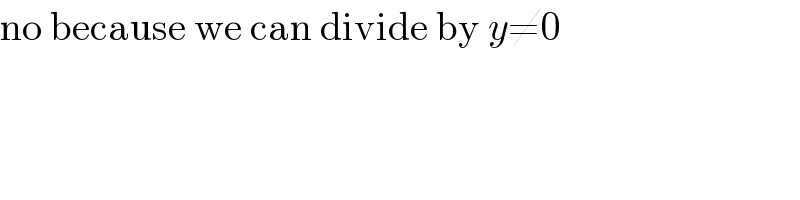
$$\mathrm{no}\:\mathrm{because}\:\mathrm{we}\:\mathrm{can}\:\mathrm{divide}\:\mathrm{by}\:{y}\neq\mathrm{0} \\ $$
Commented by john santu last updated on 26/Jan/20
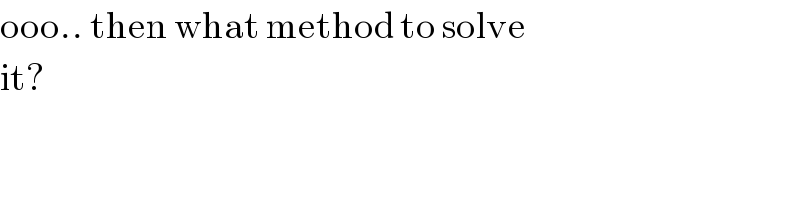
$$\mathrm{ooo}..\:\mathrm{then}\:\mathrm{what}\:\mathrm{method}\:\mathrm{to}\:\mathrm{solve} \\ $$$$\mathrm{it}? \\ $$
Commented by MJS last updated on 26/Jan/20
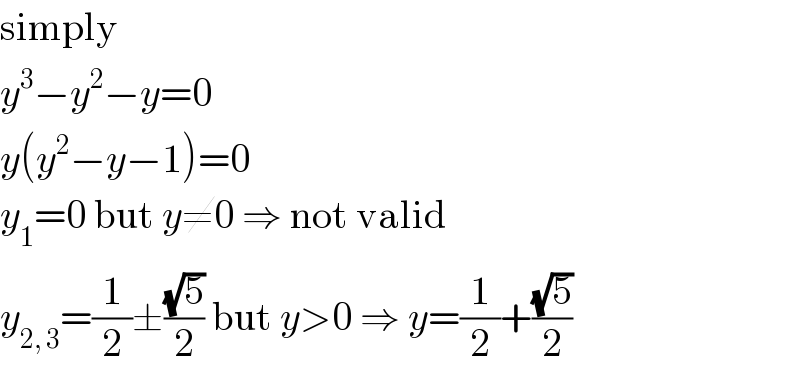
$$\mathrm{simply} \\ $$$${y}^{\mathrm{3}} −{y}^{\mathrm{2}} −{y}=\mathrm{0} \\ $$$${y}\left({y}^{\mathrm{2}} −{y}−\mathrm{1}\right)=\mathrm{0} \\ $$$${y}_{\mathrm{1}} =\mathrm{0}\:\mathrm{but}\:{y}\neq\mathrm{0}\:\Rightarrow\:\mathrm{not}\:\mathrm{valid} \\ $$$${y}_{\mathrm{2},\:\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\:\mathrm{but}\:{y}>\mathrm{0}\:\Rightarrow\:{y}=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$
Commented by TawaTawa last updated on 26/Jan/20
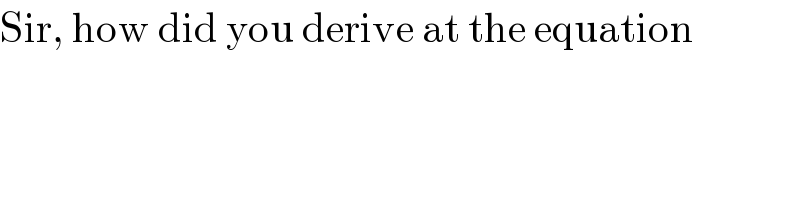
$$\mathrm{Sir},\:\mathrm{how}\:\mathrm{did}\:\mathrm{you}\:\mathrm{derive}\:\mathrm{at}\:\mathrm{the}\:\mathrm{equation} \\ $$
Commented by MJS last updated on 26/Jan/20

$$\mathrm{look}\:\mathrm{above} \\ $$
Commented by TawaTawa last updated on 26/Jan/20

$$\mathrm{I}\:\mathrm{understand}\:\mathrm{now}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
