Question Number 181415 by Socracious last updated on 24/Nov/22

$$\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{solve}}\:\:\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{x}} \\ $$$$\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}} } =\mathrm{36} \\ $$$$ \\ $$
Commented by Frix last updated on 25/Nov/22

$$\mathrm{Approximation}\:\mathrm{gives}\:{x}\approx\mathrm{2}.\mathrm{10703646396} \\ $$
Commented by Frix last updated on 25/Nov/22

$$\mathrm{There}'\mathrm{s}\:\mathrm{no}\:\mathrm{exact}\:\mathrm{solution}. \\ $$
Commented by Socracious last updated on 25/Nov/22

$$\mathrm{please}\:\mathrm{show}\:\mathrm{full}\:\mathrm{solution} \\ $$
Answered by yogamulyadi last updated on 25/Nov/22

$${x}^{{x}^{{x}} } =\left(\mathrm{6}^{{n}} \right)^{\frac{\mathrm{2}}{\mathrm{2}}\left(\mathrm{6}^{{n}} \right)^{\left(\mathrm{6}^{{n}} \right)} } \\ $$$${x}=\mathrm{6}^{{n}} \\ $$
Commented by Frix last updated on 25/Nov/22
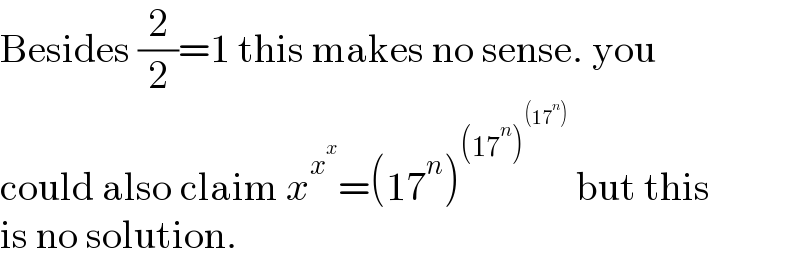
$$\mathrm{Besides}\:\frac{\mathrm{2}}{\mathrm{2}}=\mathrm{1}\:\mathrm{this}\:\mathrm{makes}\:\mathrm{no}\:\mathrm{sense}.\:\mathrm{you} \\ $$$$\mathrm{could}\:\mathrm{also}\:\mathrm{claim}\:{x}^{{x}^{{x}} } =\left(\mathrm{17}^{{n}} \right)^{\left(\mathrm{17}^{{n}} \right)^{\left(\mathrm{17}^{{n}} \right)} } \:\mathrm{but}\:\mathrm{this} \\ $$$$\mathrm{is}\:\mathrm{no}\:\mathrm{solution}. \\ $$
