Solve-for-x-y-3x-gt-2y-2x-lt-3y-where-x-y-N-

Question Number 62372 by Rasheed.Sindhi last updated on 20/Jun/19

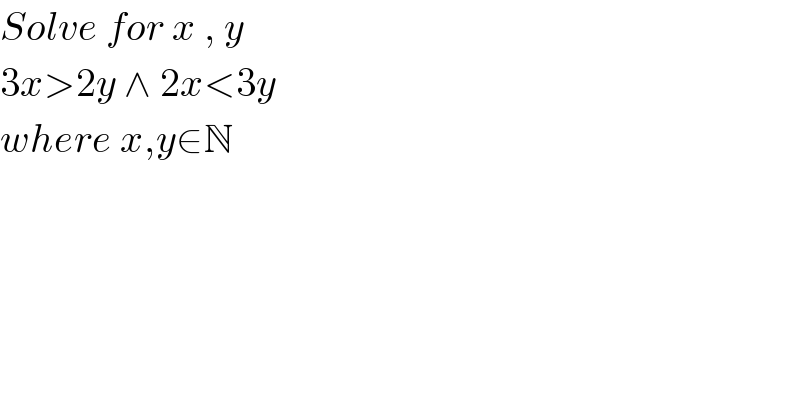
$${Solve}\:{for}\:{x}\:,\:{y} \\ $$$$\mathrm{3}{x}>\mathrm{2}{y}\:\wedge\:\mathrm{2}{x}<\mathrm{3}{y}\: \\ $$$${where}\:{x},{y}\in\mathbb{N} \\ $$

Answered by MJS last updated on 20/Jun/19

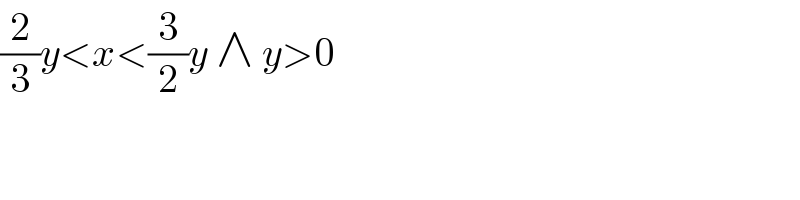
$$\frac{\mathrm{2}}{\mathrm{3}}{y}<{x}<\frac{\mathrm{3}}{\mathrm{2}}{y}\:\wedge\:{y}>\mathrm{0} \\ $$

Commented by Rasheed.Sindhi last updated on 20/Jun/19

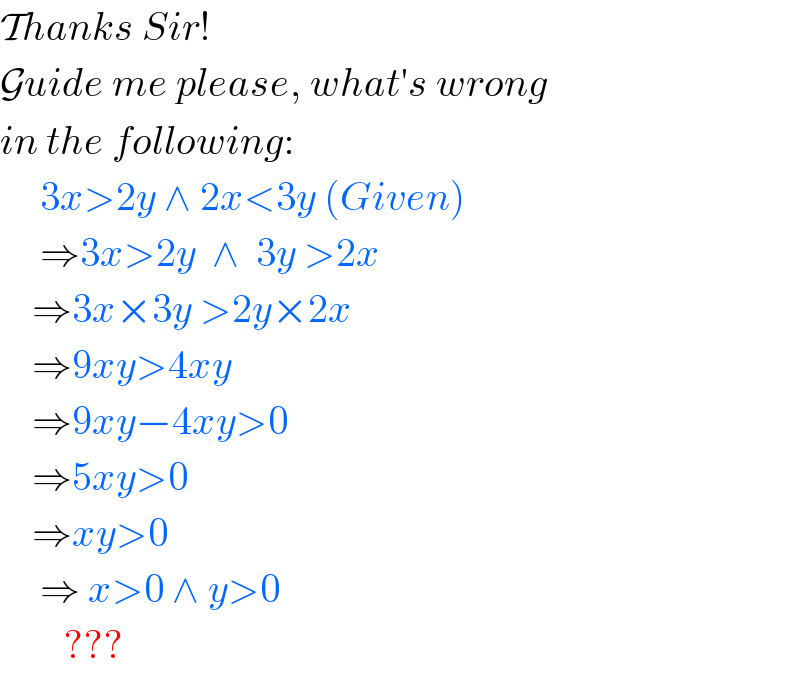
$$\mathcal{T}{hanks}\:{Sir}! \\ $$$$\mathcal{G}{uide}\:{me}\:{please},\:{what}'{s}\:{wrong} \\ $$$${in}\:{the}\:{following}: \\ $$$$\:\:\:\:\:\mathrm{3}{x}>\mathrm{2}{y}\:\wedge\:\mathrm{2}{x}<\mathrm{3}{y}\:\left({Given}\right) \\ $$$$\:\:\:\:\:\Rightarrow\mathrm{3}{x}>\mathrm{2}{y}\:\:\wedge\:\:\mathrm{3}{y}\:>\mathrm{2}{x} \\ $$$$\:\:\:\:\Rightarrow\mathrm{3}{x}×\mathrm{3}{y}\:>\mathrm{2}{y}×\mathrm{2}{x} \\ $$$$\:\:\:\:\Rightarrow\mathrm{9}{xy}>\mathrm{4}{xy} \\ $$$$\:\:\:\:\Rightarrow\mathrm{9}{xy}−\mathrm{4}{xy}>\mathrm{0} \\ $$$$\:\:\:\:\Rightarrow\mathrm{5}{xy}>\mathrm{0} \\ $$$$\:\:\:\:\Rightarrow{xy}>\mathrm{0} \\ $$$$\:\:\:\:\:\Rightarrow\:{x}>\mathrm{0}\:\wedge\:{y}>\mathrm{0}\: \\ $$$$\:\:\:\:\:\:\:\:??? \\ $$

Commented by MJS last updated on 20/Jun/19

$${xy}>\mathrm{0}\:\nRightarrow\:{x}>\mathrm{0}\wedge{y}>\mathrm{0}\:!!! \\ $$$$ \\ $$$$\mathrm{3}{x}>\mathrm{2}{y}\:\Rightarrow\:{x}>\frac{\mathrm{2}}{\mathrm{3}}{y} \\ $$$$\mathrm{3}{y}>\mathrm{2}{x}\:\Rightarrow\:{x}<\frac{\mathrm{3}}{\mathrm{2}}{y} \\ $$$$\Rightarrow\:\frac{\mathrm{2}}{\mathrm{3}}{y}<{x}<\frac{\mathrm{3}}{\mathrm{2}}{y} \\ $$$$\mathrm{1}.\:\mathrm{obviously}\:{x}\neq\mathrm{0}\:\wedge\:{y}\neq\mathrm{0} \\ $$$$\mathrm{2}.\:{x}<\mathrm{0}\:\wedge\:{y}<\mathrm{0} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}>\frac{{x}}{{y}}>\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\left.\Rightarrow\:\frac{{x}}{{y}}\in\right]−\infty;\:\frac{\mathrm{2}}{\mathrm{3}}\left[\cap\right]\frac{\mathrm{3}}{\mathrm{2}};\:+\infty\left[=\left\{\right\}\right. \\ $$$$\Rightarrow\:\mathrm{no}\:\mathrm{solution} \\ $$$$\mathrm{3}.\:{x}<\mathrm{0}\:\wedge\:{y}>\mathrm{0} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}<\frac{{x}}{{y}}<\frac{\mathrm{3}}{\mathrm{2}}\:\left(\mathrm{with}\:\frac{{x}}{{y}}<\mathrm{0}\right) \\ $$$$\Rightarrow\:\mathrm{no}\:\mathrm{solution} \\ $$$$\mathrm{4}.\:{x}>\mathrm{0}\:\wedge\:{y}<\mathrm{0} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}>\frac{{x}}{{y}}>\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\left.\Rightarrow\:\frac{{x}}{{y}}\in\right]−\infty;\:\frac{\mathrm{2}}{\mathrm{3}}\left[\cap\right]\frac{\mathrm{3}}{\mathrm{2}};\:+\infty\left[=\left\{\right\}\right. \\ $$$$\Rightarrow\:\mathrm{no}\:\mathrm{solution} \\ $$$$\mathrm{5}.\:{x}>\mathrm{0}\:\wedge\:{y}>\mathrm{0} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}<\frac{{x}}{{y}}<\frac{\mathrm{3}}{\mathrm{2}}\:\Leftrightarrow\:\frac{\mathrm{2}}{\mathrm{3}}{y}<{x}<\frac{\mathrm{3}}{\mathrm{2}}{y}\:\Leftrightarrow\:\frac{\mathrm{2}}{\mathrm{3}}{x}<{y}<\frac{\mathrm{3}}{\mathrm{2}}{x} \\ $$

Commented by Rasheed.Sindhi last updated on 20/Jun/19

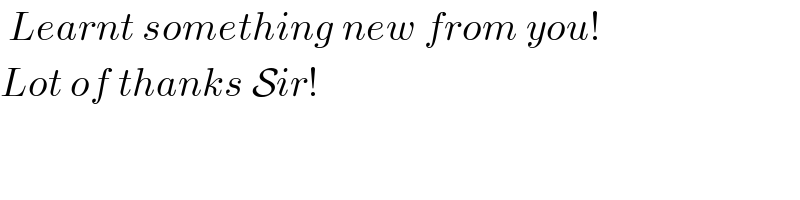
$$\:{Learnt}\:{something}\:{new}\:{from}\:{you}! \\ $$$${Lot}\:{of}\:{thanks}\:\mathcal{S}{ir}! \\ $$

Commented by MJS last updated on 20/Jun/19

$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome} \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com