Question Number 112053 by MJS_new last updated on 05/Sep/20
![solve for x, y, z ∈C: 2x^2 −3x=(√(13x^2 −52x+40)) 6y^2 −14x=(√(x^2 −220x+300)) z^2 −2z=(√(−12x^2 +72x−132)) [exact solutions possible in all cases]](https://www.tinkutara.com/question/Q112053.png)
$$\mathrm{solve}\:\mathrm{for}\:{x},\:{y},\:{z}\:\in\mathbb{C}: \\ $$$$\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}=\sqrt{\mathrm{13}{x}^{\mathrm{2}} −\mathrm{52}{x}+\mathrm{40}} \\ $$$$\mathrm{6}{y}^{\mathrm{2}} −\mathrm{14}{x}=\sqrt{{x}^{\mathrm{2}} −\mathrm{220}{x}+\mathrm{300}} \\ $$$${z}^{\mathrm{2}} −\mathrm{2}{z}=\sqrt{−\mathrm{12}{x}^{\mathrm{2}} +\mathrm{72}{x}−\mathrm{132}} \\ $$$$\left[\mathrm{exact}\:\mathrm{solutions}\:\mathrm{possible}\:\mathrm{in}\:\mathrm{all}\:\mathrm{cases}\right] \\ $$
Commented by MJS_new last updated on 06/Sep/20

$$\mathrm{beware}\:\mathrm{of}\:\mathrm{false}\:\mathrm{solutions}\:\mathrm{due}\:\mathrm{to}\:\mathrm{squaring}! \\ $$
Answered by john santu last updated on 06/Sep/20
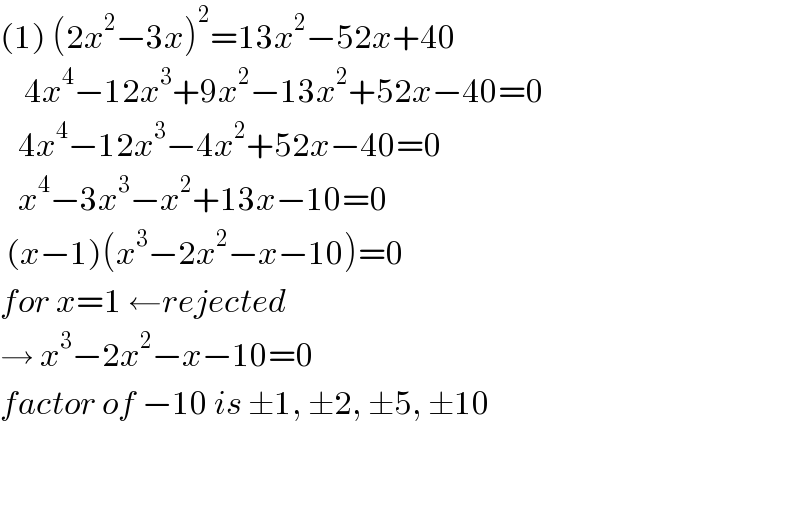
$$\left(\mathrm{1}\right)\:\left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{3}{x}\right)^{\mathrm{2}} =\mathrm{13}{x}^{\mathrm{2}} −\mathrm{52}{x}+\mathrm{40} \\ $$$$\:\:\:\:\mathrm{4}{x}^{\mathrm{4}} −\mathrm{12}{x}^{\mathrm{3}} +\mathrm{9}{x}^{\mathrm{2}} −\mathrm{13}{x}^{\mathrm{2}} +\mathrm{52}{x}−\mathrm{40}=\mathrm{0} \\ $$$$\:\:\:\mathrm{4}{x}^{\mathrm{4}} −\mathrm{12}{x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} +\mathrm{52}{x}−\mathrm{40}=\mathrm{0} \\ $$$$\:\:\:{x}^{\mathrm{4}} −\mathrm{3}{x}^{\mathrm{3}} −{x}^{\mathrm{2}} +\mathrm{13}{x}−\mathrm{10}=\mathrm{0} \\ $$$$\:\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} −{x}−\mathrm{10}\right)=\mathrm{0} \\ $$$${for}\:{x}=\mathrm{1}\:\leftarrow{rejected} \\ $$$$\rightarrow\:{x}^{\mathrm{3}} −\mathrm{2}{x}^{\mathrm{2}} −{x}−\mathrm{10}=\mathrm{0} \\ $$$${factor}\:{of}\:−\mathrm{10}\:{is}\:\pm\mathrm{1},\:\pm\mathrm{2},\:\pm\mathrm{5},\:\pm\mathrm{10} \\ $$$$ \\ $$$$ \\ $$
