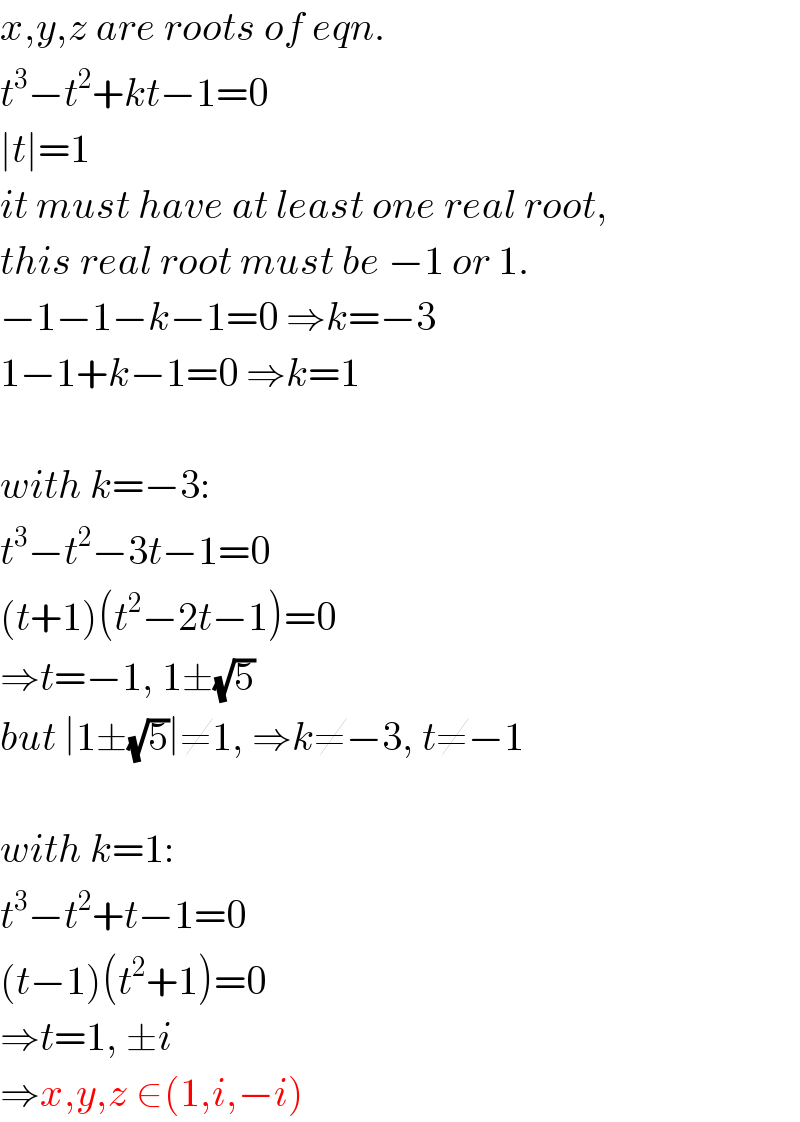Menu Close

solve-for-x-y-z-C-such-that-x-y-z-1-x-y-z-1-xyz-1-

Tinku Tara 0 Comments
Pin




Question Number 95062 by mr W last updated on 22/May/20
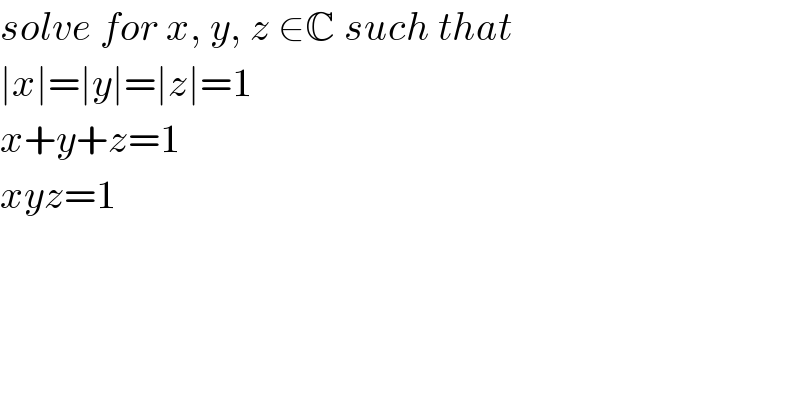
solve for x, y, z ∈C such that ∣x∣=∣y∣=∣z∣=1 x+y+z=1 xyz=1
solveforx,y,z∈Csuchthat∣x∣=∣y∣=∣z∣=1x+y+z=1xyz=1
Commented by EmericGent last updated on 22/May/20
BlackPenRedPen solved it today ^^ (1;i;-i)
Commented by mr W last updated on 23/May/20
maybe other people have other methods. basically almost all existing questions in the world have already solutions. if only questions, which are not yet solved, are interesting for this forum, then we can close it right now.
maybeotherpeoplehaveothermethods.basicallyalmostallexistingquestionsintheworldhavealreadysolutions.ifonlyquestions,whicharenotyetsolved,areinterestingforthisforum,thenwecancloseitrightnow.
Commented by EmericGent last updated on 22/May/20
I know, but posted the video this morning
Commented by mr W last updated on 22/May/20
do you have a solution? i′m interested. interesting is it when different people take different ways to solve the same problem.
doyouhaveasolution?i′minterested.interestingisitwhendifferentpeopletakedifferentwaystosolvethesameproblem.
Commented by prakash jain last updated on 23/May/20
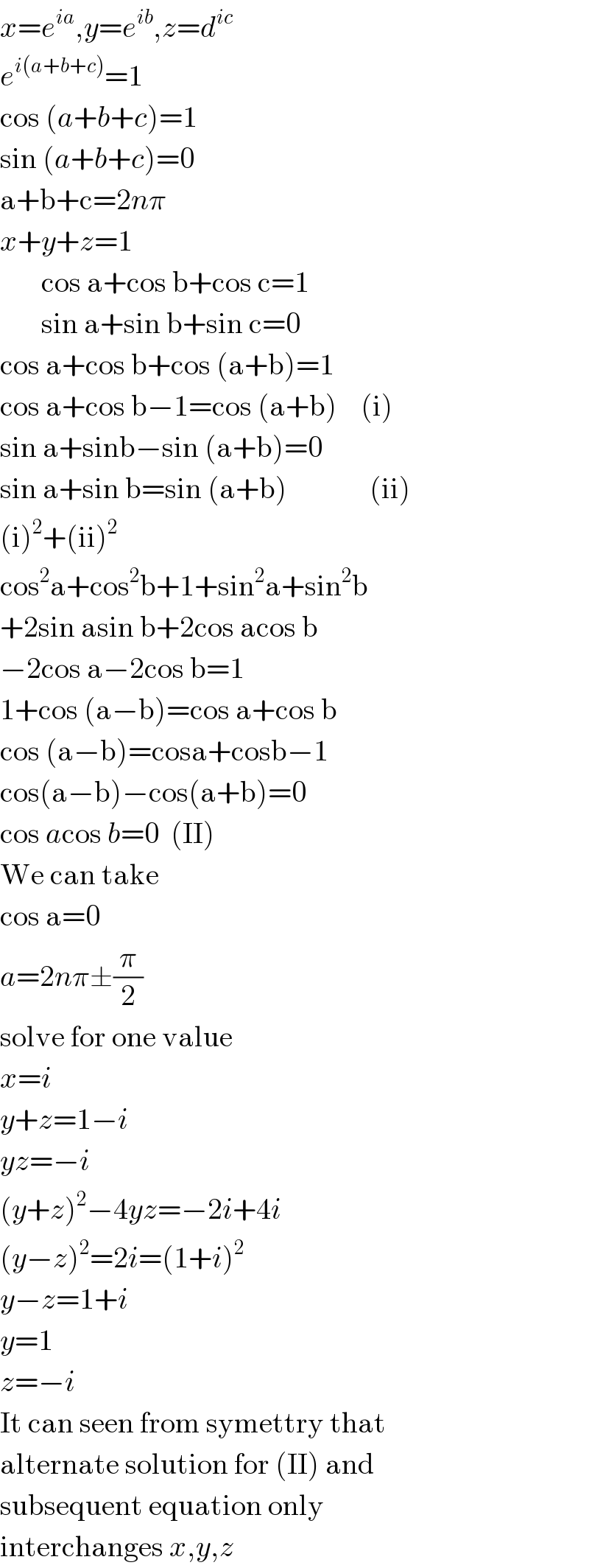
x=e^(ia) ,y=e^(ib) ,z=d^(ic) e^(i(a+b+c)) =1 cos (a+b+c)=1 sin (a+b+c)=0 a+b+c=2nπ x+y+z=1 cos a+cos b+cos c=1 sin a+sin b+sin c=0 cos a+cos b+cos (a+b)=1 cos a+cos b−1=cos (a+b) (i) sin a+sinb−sin (a+b)=0 sin a+sin b=sin (a+b) (ii) (i)^2 +(ii)^2 cos^2 a+cos^2 b+1+sin^2 a+sin^2 b +2sin asin b+2cos acos b −2cos a−2cos b=1 1+cos (a−b)=cos a+cos b cos (a−b)=cosa+cosb−1 cos(a−b)−cos(a+b)=0 cos acos b=0 (II) We can take cos a=0 a=2nπ±(π/2) solve for one value x=i y+z=1−i yz=−i (y+z)^2 −4yz=−2i+4i (y−z)^2 =2i=(1+i)^2 y−z=1+i y=1 z=−i It can seen from symettry that alternate solution for (II) and subsequent equation only interchanges x,y,z
x=eia,y=eib,z=dicei(a+b+c)=1cos(a+b+c)=1sin(a+b+c)=0a+b+c=2nπx+y+z=1cosa+cosb+cosc=1sina+sinb+sinc=0cosa+cosb+cos(a+b)=1cosa+cosb−1=cos(a+b)(i)sina+sinb−sin(a+b)=0sina+sinb=sin(a+b)(ii)(i)2+(ii)2cos2a+cos2b+1+sin2a+sin2b+2sinasinb+2cosacosb−2cosa−2cosb=11+cos(a−b)=cosa+cosbcos(a−b)=cosa+cosb−1cos(a−b)−cos(a+b)=0cosacosb=0(II)Wecantakecosa=0a=2nπ±π2solveforonevaluex=iy+z=1−iyz=−i(y+z)2−4yz=−2i+4i(y−z)2=2i=(1+i)2y−z=1+iy=1z=−iItcanseenfromsymettrythatalternatesolutionfor(II)andsubsequentequationonlyinterchangesx,y,z
Commented by mr W last updated on 23/May/20
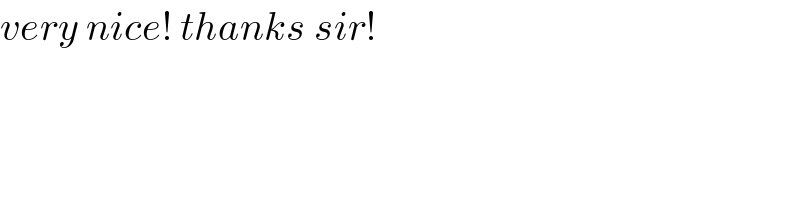
very nice! thanks sir!
verynice!thankssir!
Commented by mr W last updated on 23/May/20
x,y,z are roots of eqn. t^3 −t^2 +kt−1=0 ∣t∣=1 it must have at least one real root, this real root must be −1 or 1. −1−1−k−1=0 ⇒k=−3 1−1+k−1=0 ⇒k=1 with k=−3: t^3 −t^2 −3t−1=0 (t+1)(t^2 −2t−1)=0 ⇒t=−1, 1±(√5) but ∣1±(√5)∣≠1, ⇒k≠−3, t≠−1 with k=1: t^3 −t^2 +t−1=0 (t−1)(t^2 +1)=0 ⇒t=1, ±i ⇒x,y,z ∈(1,i,−i)
x,y,zarerootsofeqn.t3−t2+kt−1=0∣t∣=1itmusthaveatleastonerealroot,thisrealrootmustbe−1or1.−1−1−k−1=0⇒k=−31−1+k−1=0⇒k=1withk=−3:t3−t2−3t−1=0(t+1)(t2−2t−1)=0⇒t=−1,1±5but∣1±5∣≠1,⇒k≠−3,t≠−1withk=1:t3−t2+t−1=0(t−1)(t2+1)=0⇒t=1,±i⇒x,y,z∈(1,i,−i)

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *