Question Number 50580 by behi83417@gmail.com last updated on 17/Dec/18
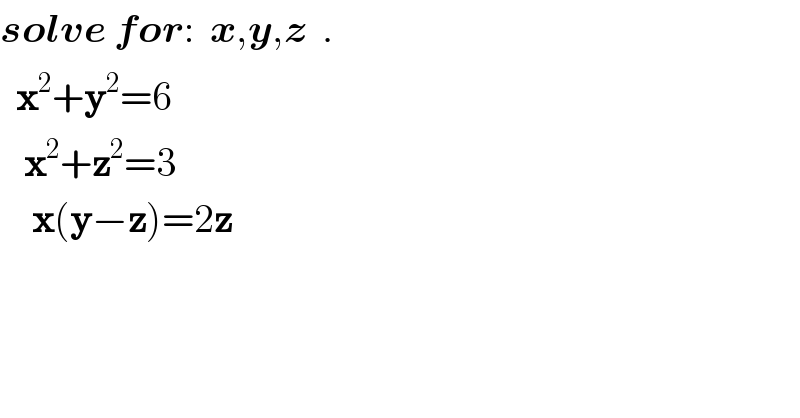
$$\boldsymbol{{solve}}\:\boldsymbol{{for}}:\:\:\boldsymbol{{x}},\boldsymbol{{y}},\boldsymbol{{z}}\:\:. \\ $$$$\:\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{y}}^{\mathrm{2}} =\mathrm{6} \\ $$$$\:\:\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{z}}^{\mathrm{2}} =\mathrm{3} \\ $$$$\:\:\:\:\boldsymbol{\mathrm{x}}\left(\boldsymbol{\mathrm{y}}−\boldsymbol{\mathrm{z}}\right)=\mathrm{2}\boldsymbol{\mathrm{z}} \\ $$
Answered by peter frank last updated on 17/Dec/18
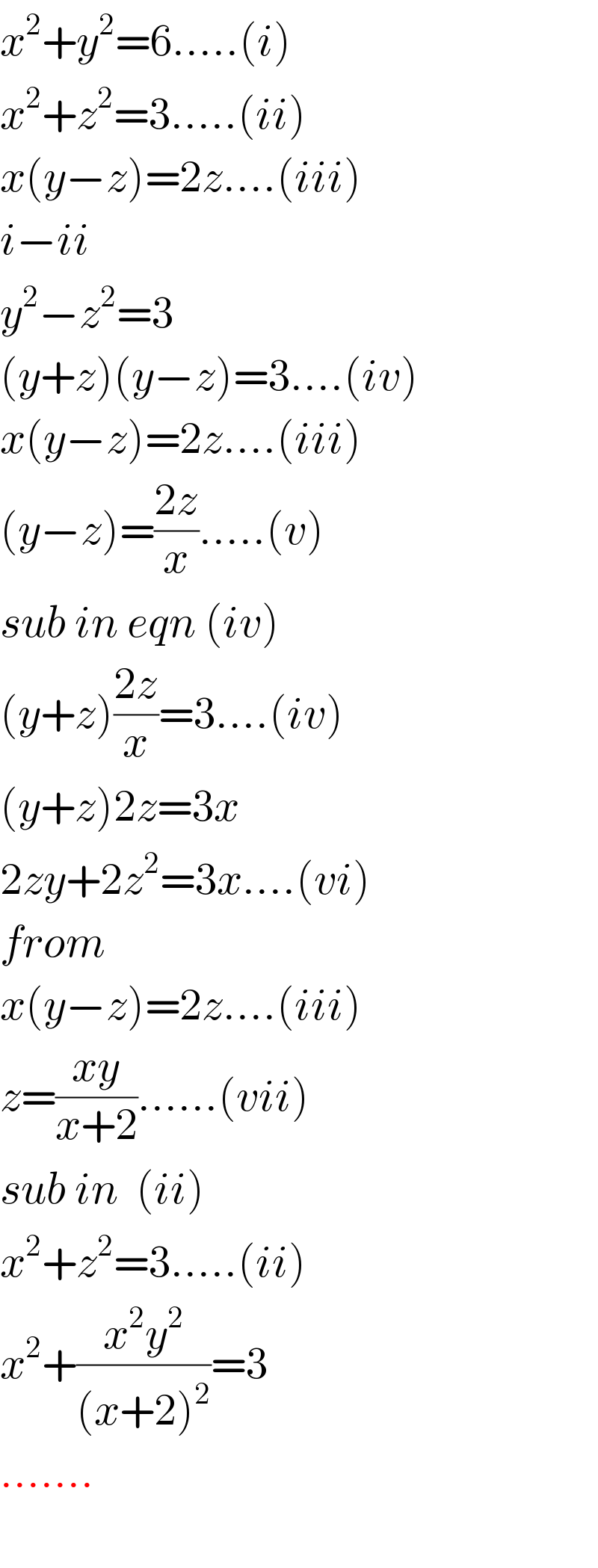
$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{6}…..\left({i}\right) \\ $$$${x}^{\mathrm{2}} +{z}^{\mathrm{2}} =\mathrm{3}…..\left({ii}\right) \\ $$$${x}\left({y}−{z}\right)=\mathrm{2}{z}….\left({iii}\right) \\ $$$${i}−{ii} \\ $$$${y}^{\mathrm{2}} −{z}^{\mathrm{2}} =\mathrm{3} \\ $$$$\left({y}+{z}\right)\left({y}−{z}\right)=\mathrm{3}….\left({iv}\right) \\ $$$${x}\left({y}−{z}\right)=\mathrm{2}{z}….\left({iii}\right) \\ $$$$\left({y}−{z}\right)=\frac{\mathrm{2}{z}}{{x}}…..\left({v}\right) \\ $$$${sub}\:{in}\:{eqn}\:\left({iv}\right) \\ $$$$\left({y}+{z}\right)\frac{\mathrm{2}{z}}{{x}}=\mathrm{3}….\left({iv}\right) \\ $$$$\left({y}+{z}\right)\mathrm{2}{z}=\mathrm{3}{x} \\ $$$$\mathrm{2}{zy}+\mathrm{2}{z}^{\mathrm{2}} =\mathrm{3}{x}….\left({vi}\right) \\ $$$${from} \\ $$$${x}\left({y}−{z}\right)=\mathrm{2}{z}….\left({iii}\right) \\ $$$${z}=\frac{{xy}}{{x}+\mathrm{2}}……\left({vii}\right) \\ $$$${sub}\:{in}\:\:\left({ii}\right) \\ $$$${x}^{\mathrm{2}} +{z}^{\mathrm{2}} =\mathrm{3}…..\left({ii}\right) \\ $$$${x}^{\mathrm{2}} +\frac{{x}^{\mathrm{2}} {y}^{\mathrm{2}} }{\left({x}+\mathrm{2}\right)^{\mathrm{2}} }=\mathrm{3} \\ $$$$……. \\ $$$$ \\ $$
Answered by ajfour last updated on 17/Dec/18
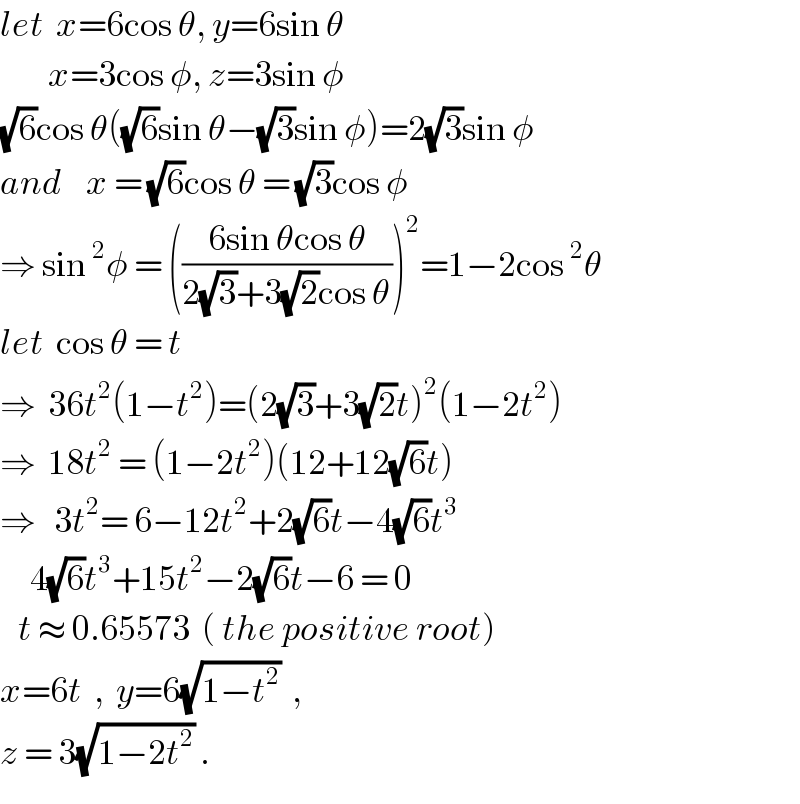
$${let}\:\:{x}=\mathrm{6cos}\:\theta,\:{y}=\mathrm{6sin}\:\theta \\ $$$$\:\:\:\:\:\:\:\:{x}=\mathrm{3cos}\:\phi,\:{z}=\mathrm{3sin}\:\phi \\ $$$$\sqrt{\mathrm{6}}\mathrm{cos}\:\theta\left(\sqrt{\mathrm{6}}\mathrm{sin}\:\theta−\sqrt{\mathrm{3}}\mathrm{sin}\:\phi\right)=\mathrm{2}\sqrt{\mathrm{3}}\mathrm{sin}\:\phi \\ $$$${and}\:\:\:\:{x}\:=\:\sqrt{\mathrm{6}}\mathrm{cos}\:\theta\:=\:\sqrt{\mathrm{3}}\mathrm{cos}\:\phi \\ $$$$\Rightarrow\:\mathrm{sin}\:^{\mathrm{2}} \phi\:=\:\left(\frac{\mathrm{6sin}\:\theta\mathrm{cos}\:\theta}{\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{3}\sqrt{\mathrm{2}}\mathrm{cos}\:\theta}\right)^{\mathrm{2}} =\mathrm{1}−\mathrm{2cos}\:^{\mathrm{2}} \theta \\ $$$${let}\:\:\mathrm{cos}\:\theta\:=\:{t} \\ $$$$\Rightarrow\:\:\mathrm{36}{t}^{\mathrm{2}} \left(\mathrm{1}−{t}^{\mathrm{2}} \right)=\left(\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{3}\sqrt{\mathrm{2}}{t}\right)^{\mathrm{2}} \left(\mathrm{1}−\mathrm{2}{t}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:\:\mathrm{18}{t}^{\mathrm{2}} \:=\:\left(\mathrm{1}−\mathrm{2}{t}^{\mathrm{2}} \right)\left(\mathrm{12}+\mathrm{12}\sqrt{\mathrm{6}}{t}\right) \\ $$$$\Rightarrow\:\:\:\mathrm{3}{t}^{\mathrm{2}} =\:\mathrm{6}−\mathrm{12}{t}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{6}}{t}−\mathrm{4}\sqrt{\mathrm{6}}{t}^{\mathrm{3}} \\ $$$$\:\:\:\:\:\mathrm{4}\sqrt{\mathrm{6}}{t}^{\mathrm{3}} +\mathrm{15}{t}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{6}}{t}−\mathrm{6}\:=\:\mathrm{0} \\ $$$$\:\:\:{t}\:\approx\:\mathrm{0}.\mathrm{65573}\:\:\left(\:{the}\:{positive}\:{root}\right) \\ $$$${x}=\mathrm{6}{t}\:\:,\:\:{y}=\mathrm{6}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }\:\:,\: \\ $$$${z}\:=\:\mathrm{3}\sqrt{\mathrm{1}−\mathrm{2}{t}^{\mathrm{2}} }\:. \\ $$
Commented by behi83417@gmail.com last updated on 17/Dec/18

$$\left(\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{3}\sqrt{\mathrm{2}}{t}\right)^{\mathrm{2}} \:\:\:? \\ $$
Commented by peter frank last updated on 17/Dec/18
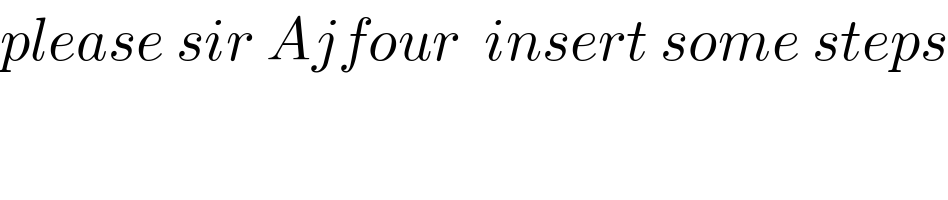
$${please}\:{sir}\:{Ajfour}\:\:{insert}\:{some}\:{steps} \\ $$
Commented by ajfour last updated on 17/Dec/18

$${did}.. \\ $$
Commented by peter frank last updated on 17/Dec/18

$${thank}\:{you} \\ $$
