Question Number 60980 by Tawa1 last updated on 28/May/19
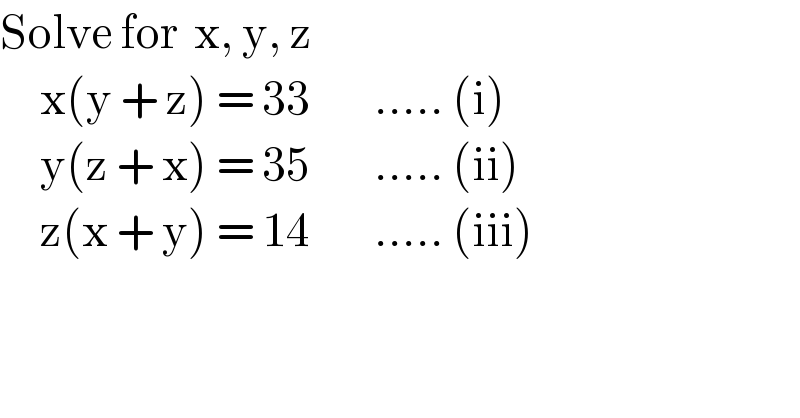
$$\mathrm{Solve}\:\mathrm{for}\:\:\mathrm{x},\:\mathrm{y},\:\mathrm{z} \\ $$$$\:\:\:\:\:\mathrm{x}\left(\mathrm{y}\:+\:\mathrm{z}\right)\:=\:\mathrm{33}\:\:\:\:\:\:\:\:…..\:\left(\mathrm{i}\right) \\ $$$$\:\:\:\:\:\mathrm{y}\left(\mathrm{z}\:+\:\mathrm{x}\right)\:=\:\mathrm{35}\:\:\:\:\:\:\:\:…..\:\left(\mathrm{ii}\right) \\ $$$$\:\:\:\:\:\mathrm{z}\left(\mathrm{x}\:+\:\mathrm{y}\right)\:=\:\mathrm{14}\:\:\:\:\:\:\:\:…..\:\left(\mathrm{iii}\right) \\ $$
Commented by Prithwish sen last updated on 28/May/19

$$\mathrm{Adding}\:\left(\mathrm{i}\right),\left(\mathrm{ii}\right)\:\mathrm{and}\:\left(\mathrm{iii}\right) \\ $$$$\mathrm{xy}+\mathrm{xz}+\mathrm{yz}=\mathrm{41}….\left(\mathrm{iv}\right) \\ $$$$\left(\mathrm{iv}\right)−\left(\mathrm{i}\right)\:\Rightarrow\mathrm{yz}=\mathrm{8}….\left(\mathrm{v}\right) \\ $$$$\left(\mathrm{iv}\right)−\left(\mathrm{ii}\right)\Rightarrow\mathrm{xz}=\mathrm{6}…\left(\mathrm{vi}\right) \\ $$$$\left(\mathrm{iv}\right)−\left(\mathrm{iii}\right)\Rightarrow\mathrm{xy}=\mathrm{27}….\left(\mathrm{vii}\right) \\ $$$$\mathrm{Now} \\ $$$$\mathrm{multiplying}\:\mathrm{v},\mathrm{vi}\:\mathrm{and}\:\mathrm{vii} \\ $$$$\left(\mathrm{xyz}\right)^{\mathrm{2}} =\mathrm{6}×\mathrm{8}×\mathrm{27}=\left(\mathrm{36}\right)^{\mathrm{2}} \\ $$$$\mathrm{xyz}=\pm\mathrm{36}….\left(\mathrm{viii}\right) \\ $$$$\frac{\left(\mathrm{viii}\right)}{\left(\mathrm{v}\right)}\:\Rightarrow\mathrm{x}=\frac{\pm\mathrm{36}}{\mathrm{8}}=\pm\frac{\mathrm{9}}{\mathrm{2}} \\ $$$$\mathrm{Similarly} \\ $$$$\mathrm{y}=\pm\mathrm{6},\:\mathrm{z}=\pm\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Tawa1 last updated on 28/May/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by tanmay last updated on 28/May/19
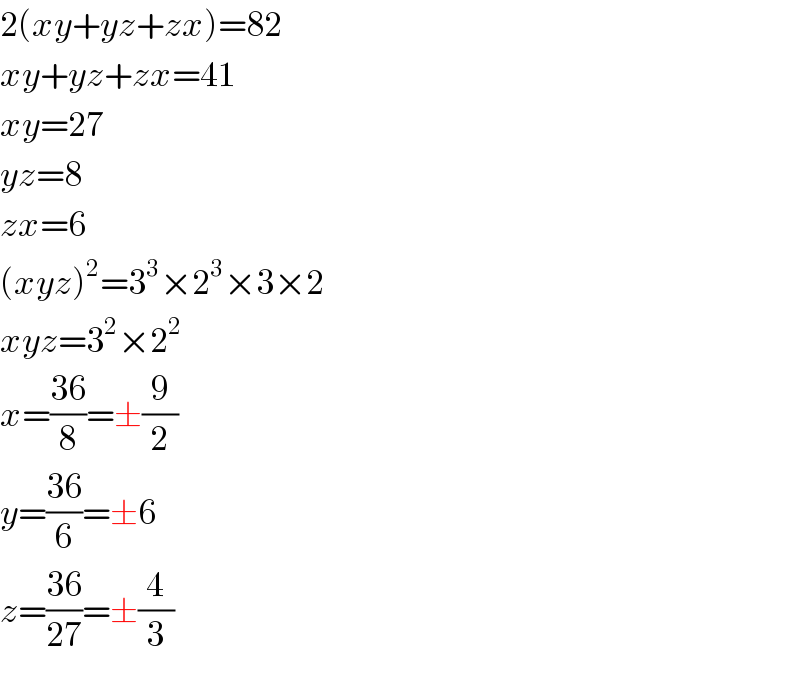
$$\mathrm{2}\left({xy}+{yz}+{zx}\right)=\mathrm{82} \\ $$$${xy}+{yz}+{zx}=\mathrm{41} \\ $$$${xy}=\mathrm{27} \\ $$$${yz}=\mathrm{8} \\ $$$${zx}=\mathrm{6} \\ $$$$\left({xyz}\right)^{\mathrm{2}} =\mathrm{3}^{\mathrm{3}} ×\mathrm{2}^{\mathrm{3}} ×\mathrm{3}×\mathrm{2} \\ $$$${xyz}=\mathrm{3}^{\mathrm{2}} ×\mathrm{2}^{\mathrm{2}} \\ $$$${x}=\frac{\mathrm{36}}{\mathrm{8}}=\pm\frac{\mathrm{9}}{\mathrm{2}} \\ $$$${y}=\frac{\mathrm{36}}{\mathrm{6}}=\pm\mathrm{6} \\ $$$${z}=\frac{\mathrm{36}}{\mathrm{27}}=\pm\frac{\mathrm{4}}{\mathrm{3}} \\ $$
Commented by Tawa1 last updated on 28/May/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
