Question Number 61591 by MJS last updated on 05/Jun/19

$$\mathrm{solve}\:\mathrm{for}\:{z}\in\mathbb{C} \\ $$$$\sqrt[{\mathrm{2}}]{{z}}=−\mathrm{1} \\ $$$$\sqrt[{\mathrm{3}}]{{z}}=−\mathrm{1} \\ $$$$\sqrt[{\mathrm{4}}]{{z}}=−\mathrm{1} \\ $$
Commented by Smail last updated on 05/Jun/19

$$\:{saw}\:\sqrt[{\mathrm{2}}]{{z}}\:,\sqrt[{\mathrm{3}}]{{z}}=−\mathrm{1}\:{and}\:{I}\:{thought}\:{it}\:{is}\:\sqrt[{\mathrm{3}}]{\left(−\mathrm{1}\right)}\:\:\:{and}\: \\ $$$${since}\:{Iwas}\:{solving}\:{this}\:{problem}\:{in}\:{a}\:{rush} \\ $$$${I}\:{made}\:{that}\:{silly}\:{mistake}. \\ $$$${My}\:{apologies}. \\ $$
Commented by maxmathsup by imad last updated on 05/Jun/19
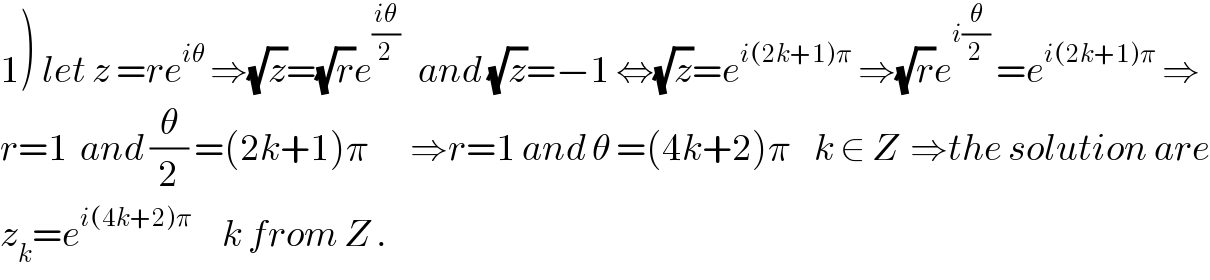
$$\left.\mathrm{1}\right)\:{let}\:{z}\:={re}^{{i}\theta} \:\Rightarrow\sqrt{{z}}=\sqrt{{r}}{e}^{\frac{{i}\theta}{\mathrm{2}}} \:\:\:{and}\:\sqrt{{z}}=−\mathrm{1}\:\Leftrightarrow\sqrt{{z}}={e}^{{i}\left(\mathrm{2}{k}+\mathrm{1}\right)\pi} \:\Rightarrow\sqrt{{r}}{e}^{{i}\frac{\theta}{\mathrm{2}}} \:={e}^{{i}\left(\mathrm{2}{k}+\mathrm{1}\right)\pi} \:\Rightarrow \\ $$$${r}=\mathrm{1}\:\:{and}\:\frac{\theta}{\mathrm{2}}\:=\left(\mathrm{2}{k}+\mathrm{1}\right)\pi\:\:\:\:\:\:\:\Rightarrow{r}=\mathrm{1}\:{and}\:\theta\:=\left(\mathrm{4}{k}+\mathrm{2}\right)\pi\:\:\:\:{k}\:\in\:{Z}\:\:\Rightarrow{the}\:{solution}\:{are} \\ $$$${z}_{{k}} ={e}^{{i}\left(\mathrm{4}{k}+\mathrm{2}\right)\pi} \:\:\:\:\:{k}\:{from}\:{Z}\:. \\ $$
Commented by Mr X pcx last updated on 05/Jun/19

$${sir}\:{smail}\:\:{z}^{\frac{\mathrm{1}}{{n}}} =−\mathrm{1}\:\Rightarrow{z}\:=\left(−\mathrm{1}\right)^{{n}} \\ $$$${if}\:{z}={e}^{{i}\pi\frac{\mathrm{2}{k}+\mathrm{1}}{{n}}} \:\:\:\Rightarrow \\ $$$${z}^{\frac{\mathrm{1}}{{n}}} ={e}^{{i}\pi\left(\frac{\mathrm{2}{k}+\mathrm{1}}{{n}^{\mathrm{2}} }\right)} \:\neq−\mathrm{1}\:{so}\:{you}\:{have} \\ $$$${commited}\:{a}\:{error}… \\ $$
Commented by MJS last updated on 05/Jun/19

$$\mathrm{this}\:\mathrm{seems}\:\mathrm{strange}\:\mathrm{to}\:\mathrm{me}… \\ $$$$ \\ $$$$\mathrm{obviously}\:\mathrm{this}\:\mathrm{is}\:\mathrm{right}: \\ $$$${z}^{{n}} ={a}\:\mathrm{with}\:{a}\in\mathbb{R}^{−} ,\:{n}\in\mathbb{N}^{\bigstar} \\ $$$${z}=\mid{a}\mid^{\frac{\mathrm{1}}{{n}}} \mathrm{e}^{\mathrm{i}\frac{−\pi+\mathrm{2}\pi{k}}{{n}}} \:\mathrm{with}\:{k}\in\mathbb{N}\wedge{k}<{n} \\ $$$$ \\ $$$${z}^{\mathrm{3}} =−\mathrm{1}\:\Rightarrow\:{z}=−\mathrm{1}\vee{z}=\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i} \\ $$$$\mathrm{testing}:\:\left(−\mathrm{1}\right)^{\mathrm{3}} =−\mathrm{1};\:\left(\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}\right)^{\mathrm{2}} =−\mathrm{1} \\ $$$$ \\ $$$$\mathrm{now}\:\mathrm{this} \\ $$$${z}^{\frac{\mathrm{1}}{{n}}} ={a}\:\mathrm{with}\:{a}\in\mathbb{R}^{−} ,\:{n}\in\mathbb{N}^{\bigstar} \\ $$$$\mathrm{should}\:\mathrm{be}\:\mathrm{similar}: \\ $$$${z}=\mid{a}\mid^{{n}} \mathrm{e}^{\mathrm{i}\left(−\pi+\mathrm{2}\pi{k}\right){n}} \:\mathrm{with}\:{k}\in\mathbb{N}\wedge{k}<\frac{\mathrm{1}}{{n}}\:\Rightarrow \\ $$$$\Rightarrow\:{k}=\mathrm{0}\:\Rightarrow\:{z}=\mid{a}\mid^{{n}} \mathrm{e}^{−\mathrm{i}\pi{n}} =\begin{cases}{−\mid{a}\mid^{{n}} \:\mathrm{with}\:{n}=\mathrm{2}{m}−\mathrm{1}}\\{\mid{a}\mid^{{n}} \:\mathrm{with}\:{n}=\mathrm{2}{m}}\end{cases};\:{m}\in\mathbb{N}^{\bigstar} \\ $$$$ \\ $$$${z}^{\frac{\mathrm{1}}{\mathrm{3}}} =−\mathrm{1}\:\Rightarrow\:{z}=−\mathrm{1} \\ $$$$\mathrm{testing}:\:\sqrt[{\mathrm{3}}]{−\mathrm{1}}=\begin{cases}{−\mathrm{1}}\\{\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}}\end{cases};\:\mathrm{so}\:\mathrm{it}'\mathrm{s}\:\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{right}\:\mathrm{and}\:\frac{\mathrm{2}}{\mathrm{3}}\:\mathrm{wrong} \\ $$$$ \\ $$$$\mathrm{and}\:\mathrm{what}\:\mathrm{about}\:\mathrm{these}: \\ $$$${z}^{\frac{\mathrm{3}}{\mathrm{2}}} =−\mathrm{1} \\ $$$${z}^{\frac{\mathrm{5}}{\mathrm{3}}} =−\mathrm{1} \\ $$$${z}^{\sqrt{\mathrm{2}}} =−\mathrm{1} \\ $$
Commented by Mr X pcx last updated on 05/Jun/19

$${henerally}\:{let}\:{solve}\:^{{n}} \sqrt{{z}}=−\mathrm{1} \\ $$$${let}\:{z}\:={re}^{{i}\theta} \:\: \\ $$$${z}^{\frac{\mathrm{1}}{{n}}} =−\mathrm{1}\:\Rightarrow{r}^{\frac{\mathrm{1}}{{n}}} \:{e}^{{i}\frac{\theta}{{n}}} \:={e}^{{i}\left(\mathrm{2}{k}+\mathrm{1}\right)\pi} \:\Rightarrow \\ $$$${r}=\mathrm{1}\:{and}\:\:\frac{\theta}{{n}}\:=\left(\mathrm{2}{k}+\mathrm{1}\right)\pi\:\Rightarrow \\ $$$$\theta_{{k}} =\left(\mathrm{2}{k}+\mathrm{1}\right){n}\pi\:\Rightarrow \\ $$$${z}_{{k}} ={e}^{{i}\left(\mathrm{2}{k}+\mathrm{1}\right){n}\pi} \:\:\:\:{with}\:{k}\:{from}\:{Z}\:. \\ $$$${but}\:{we}\:{see}\:{that}\:{z}_{{k}} ={e}^{{i}\left(\mathrm{2}{nk}\right)\pi} \:{e}^{{in}\pi} \:\Rightarrow \\ $$$${z}_{{k}} =\left(−\mathrm{1}\right)^{{n}} \:….! \\ $$
Commented by Mr X pcx last updated on 05/Jun/19

$${generally}…. \\ $$
Commented by MJS last updated on 05/Jun/19

$$\mathrm{I}\:\mathrm{have}\:\mathrm{serious}\:\mathrm{doubts}.\:\mathrm{it}\:\mathrm{seems}\:\mathrm{a}\:\mathrm{matter}\:\mathrm{of} \\ $$$$\mathrm{definition}.\:\mathrm{if}\:\mathrm{we}'\mathrm{re}\:\mathrm{not}\:\mathrm{careful}\:\mathrm{we}\:\mathrm{might}\:\mathrm{end} \\ $$$$\mathrm{up}\:\mathrm{with}\:\sqrt{\mathrm{2}}+\sqrt{\mathrm{2}}=\mathrm{0},\:\mathrm{not}\:\mathrm{to}\:\mathrm{mention}\:\mathrm{what}\:\mathrm{might} \\ $$$$\mathrm{happen}\:\mathrm{here}:\:\sqrt[{\mathrm{3}}]{−\mathrm{1}}+\sqrt[{\mathrm{3}}]{−\mathrm{1}}+\sqrt[{\mathrm{3}}]{−\mathrm{1}}=??? \\ $$
Commented by Smail last updated on 05/Jun/19

$${I}\:{am}\:{deleting}\:{my}\:{answer}\:{right}\:{now}. \\ $$
Answered by MJS last updated on 05/Jun/19

Commented by MJS last updated on 05/Jun/19

$$\mathrm{if}\:\mathrm{this}\:\mathrm{is}\:\mathrm{right}\:\left(\mathrm{I}\:\mathrm{believe}\:\mathrm{it}\:\mathrm{is}\right)\:\Rightarrow\:\mathrm{there}'\mathrm{s}\:\mathrm{no} \\ $$$${n}\in\mathbb{Z}\:\mathrm{for}\:\mathrm{some}\:\mathrm{cases}\:\Rightarrow\:\mathrm{these}\:\mathrm{cases}\:\mathrm{have}\:\mathrm{no} \\ $$$$\mathrm{solution} \\ $$$${z}^{\frac{\mathrm{1}}{{k}}} =−\mathrm{1}\:\mathrm{with}\:{z}\in\mathbb{C}\wedge{k}\in\mathbb{N}^{\bigstar} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}{k}}\leqslant{n}<\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}{k}} \\ $$$$\mathrm{this}\:\mathrm{only}\:\mathrm{has}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{for}\:{k}=\mathrm{1}\:\Rightarrow\:\mathrm{0}\leqslant{n}<\mathrm{1}\:\Rightarrow\:{n}=\mathrm{0} \\ $$
