Question Number 33823 by 33 last updated on 25/Apr/18
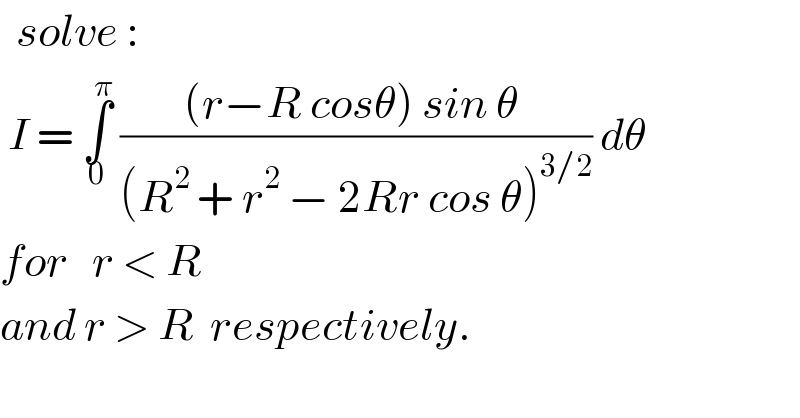
$$\:\:{solve}\::\: \\ $$$$\:{I}\:=\:\underset{\mathrm{0}} {\overset{\pi} {\int}}\:\frac{\left({r}−{R}\:{cos}\theta\right)\:{sin}\:\theta\:}{\left({R}^{\mathrm{2}\:} +\:{r}^{\mathrm{2}} \:−\:\mathrm{2}{Rr}\:{cos}\:\theta\right)^{\mathrm{3}/\mathrm{2}} }\:{d}\theta \\ $$$${for}\:\:\:{r}\:<\:{R} \\ $$$${and}\:{r}\:>\:{R}\:\:{respectively}. \\ $$
Answered by MJS last updated on 26/Apr/18
![∫u′v=uv−∫uv′ u′=((sin θ)/((r^2 +R^2 −2rRcos θ)^(3/2) )); v=r−Rcos θ u=−(1/(rR(r^2 +R^2 −2rRcos θ)^(1/2) )); v′=Rsin θ [((∫((sin θ)/((r^2 +R^2 −2rRcos θ)^(3/2) ))dθ=)),(( [t=r^2 +R^2 −2rRcos θ → dx=(dt/(2rRsin θ))])),((=(1/(2rR))∫(1/t^(3/2) )dt=−(1/(rRt^(1/2) )))) ] uv=−((r−Rcos θ)/(rR(r^2 +R^2 −2rRcos θ)^(1/2) )) −∫uv′=∫((sin θ)/(r(r^2 +R^2 −2rRcos θ)^(1/2) ))= [with the same substitution as above] =(((r^2 +R^2 −2rRcos θ)^(1/2) )/(r^2 R)) ∫(((r−Rcos θ)sin θ)/((r^2 +R^2 −2rRcos θ)^(3/2) ))= =−((r−Rcos θ)/(rR(r^2 +R^2 −2rRcos θ)^(1/2) ))+(((r^2 +R^2 −2rRcos θ)^(1/2) )/(r^2 R))+C= =((R−rcos θ)/(r^2 (√(r^2 +R^2 −2rRcos θ))))+C=F(θ) F(π)−F(0)=((R+r)/(r^2 ∣R+r∣))−((R−r)/(r^2 ∣R−r∣)) r, R>0 r<R ⇒ F(π)−F(0)=0 r>R ⇒ F(π)−F(0)=(2/r^2 )](https://www.tinkutara.com/question/Q33858.png)
$$\int{u}'{v}={uv}−\int{uv}' \\ $$$${u}'=\frac{\mathrm{sin}\:\theta}{\left({r}^{\mathrm{2}} +{R}^{\mathrm{2}} −\mathrm{2}{rR}\mathrm{cos}\:\theta\right)^{\frac{\mathrm{3}}{\mathrm{2}}} };\:{v}={r}−{R}\mathrm{cos}\:\theta \\ $$$${u}=−\frac{\mathrm{1}}{{rR}\left({r}^{\mathrm{2}} +{R}^{\mathrm{2}} −\mathrm{2}{rR}\mathrm{cos}\:\theta\right)^{\frac{\mathrm{1}}{\mathrm{2}}} };\:{v}'={R}\mathrm{sin}\:\theta \\ $$$$\:\:\:\:\:\begin{bmatrix}{\int\frac{\mathrm{sin}\:\theta}{\left({r}^{\mathrm{2}} +{R}^{\mathrm{2}} −\mathrm{2}{rR}\mathrm{cos}\:\theta\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{d}\theta=}\\{\:\:\:\:\:\left[{t}={r}^{\mathrm{2}} +{R}^{\mathrm{2}} −\mathrm{2}{rR}\mathrm{cos}\:\theta\:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{2}{rR}\mathrm{sin}\:\theta}\right]}\\{=\frac{\mathrm{1}}{\mathrm{2}{rR}}\int\frac{\mathrm{1}}{{t}^{\frac{\mathrm{3}}{\mathrm{2}}} }{dt}=−\frac{\mathrm{1}}{{rRt}^{\frac{\mathrm{1}}{\mathrm{2}}} }}\end{bmatrix} \\ $$$${uv}=−\frac{{r}−{R}\mathrm{cos}\:\theta}{{rR}\left({r}^{\mathrm{2}} +{R}^{\mathrm{2}} −\mathrm{2}{rR}\mathrm{cos}\:\theta\right)^{\frac{\mathrm{1}}{\mathrm{2}}} } \\ $$$$−\int{uv}'=\int\frac{\mathrm{sin}\:\theta}{{r}\left({r}^{\mathrm{2}} +{R}^{\mathrm{2}} −\mathrm{2}{rR}\mathrm{cos}\:\theta\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }= \\ $$$$\:\:\:\:\:\left[\mathrm{with}\:\mathrm{the}\:\mathrm{same}\:\mathrm{substitution}\:\mathrm{as}\:\mathrm{above}\right] \\ $$$$=\frac{\left({r}^{\mathrm{2}} +{R}^{\mathrm{2}} −\mathrm{2}{rR}\mathrm{cos}\:\theta\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{{r}^{\mathrm{2}} {R}} \\ $$$$\int\frac{\left({r}−{R}\mathrm{cos}\:\theta\right)\mathrm{sin}\:\theta}{\left({r}^{\mathrm{2}} +{R}^{\mathrm{2}} −\mathrm{2}{rR}\mathrm{cos}\:\theta\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }= \\ $$$$=−\frac{{r}−{R}\mathrm{cos}\:\theta}{{rR}\left({r}^{\mathrm{2}} +{R}^{\mathrm{2}} −\mathrm{2}{rR}\mathrm{cos}\:\theta\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }+\frac{\left({r}^{\mathrm{2}} +{R}^{\mathrm{2}} −\mathrm{2}{rR}\mathrm{cos}\:\theta\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{{r}^{\mathrm{2}} {R}}+{C}= \\ $$$$=\frac{{R}−{r}\mathrm{cos}\:\theta}{{r}^{\mathrm{2}} \sqrt{{r}^{\mathrm{2}} +{R}^{\mathrm{2}} −\mathrm{2}{rR}\mathrm{cos}\:\theta}}+{C}={F}\left(\theta\right) \\ $$$${F}\left(\pi\right)−{F}\left(\mathrm{0}\right)=\frac{{R}+{r}}{{r}^{\mathrm{2}} \mid{R}+{r}\mid}−\frac{{R}−{r}}{{r}^{\mathrm{2}} \mid{R}−{r}\mid} \\ $$$${r},\:{R}>\mathrm{0} \\ $$$${r}<{R}\:\Rightarrow\:{F}\left(\pi\right)−{F}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${r}>{R}\:\Rightarrow\:{F}\left(\pi\right)−{F}\left(\mathrm{0}\right)=\frac{\mathrm{2}}{{r}^{\mathrm{2}} } \\ $$
