Question Number 118196 by mathocean1 last updated on 15/Oct/20

$${solve}\:{in}\:\mathbb{N}: \\ $$$${b}^{\mathrm{3}} \left(\mathrm{2}{b}^{\mathrm{2}} +\mathrm{2}{b}+\mathrm{1}\right)=\mathrm{18360} \\ $$
Answered by Olaf last updated on 15/Oct/20
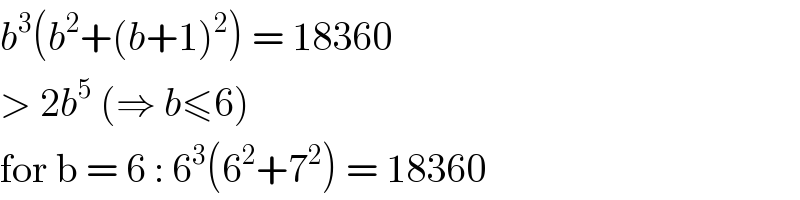
$${b}^{\mathrm{3}} \left({b}^{\mathrm{2}} +\left({b}+\mathrm{1}\right)^{\mathrm{2}} \right)\:=\:\mathrm{18360} \\ $$$$>\:\mathrm{2}{b}^{\mathrm{5}} \:\left(\Rightarrow\:{b}\leqslant\mathrm{6}\right) \\ $$$$\mathrm{for}\:\mathrm{b}\:=\:\mathrm{6}\::\:\mathrm{6}^{\mathrm{3}} \left(\mathrm{6}^{\mathrm{2}} +\mathrm{7}^{\mathrm{2}} \right)\:=\:\mathrm{18360} \\ $$
Commented by mathocean1 last updated on 15/Oct/20

$${please}\:{can}\:{you}\:{detail}\:{the}\:{second}\:{line} \\ $$
Commented by Olaf last updated on 15/Oct/20

$$\mathrm{2}{b}^{\mathrm{5}} \:\approx\overset{\mathrm{5}} {\:}\sqrt{\frac{\mathrm{18360}}{\mathrm{2}}}\:\approx\:\mathrm{6},\mathrm{02} \\ $$$$\mathrm{For}\:\mathrm{b}\:\geqslant\:\mathrm{7}\:\mathrm{expression}\:>\:\mathrm{18360} \\ $$$$\mathrm{For}\:\mathrm{b}\:=\:\mathrm{6}\:\mathrm{expression}\:=\:\mathrm{18360}\:\mathrm{OK}! \\ $$$$\mathrm{For}\:\mathrm{b}\:<\:\mathrm{6}\:\mathrm{expression}\:<\:\mathrm{18360}\: \\ $$$$ \\ $$
