Question Number 107065 by mathocean1 last updated on 08/Aug/20
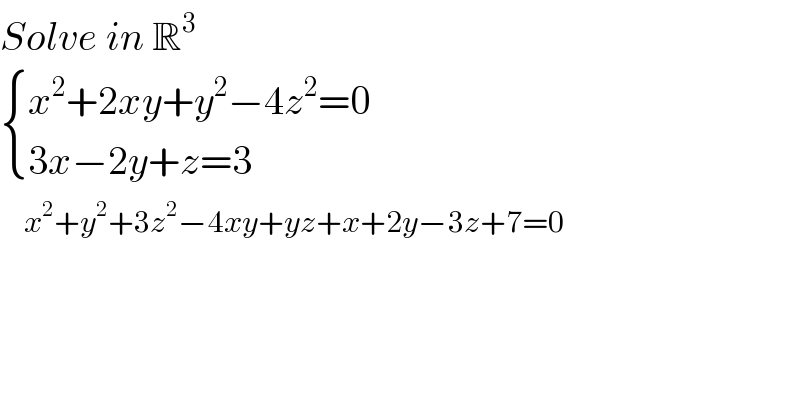
$${Solve}\:{in}\:\mathbb{R}^{\mathrm{3}} \\ $$$$\begin{cases}{{x}^{\mathrm{2}} +\mathrm{2}{xy}+{y}^{\mathrm{2}} −\mathrm{4}{z}^{\mathrm{2}} =\mathrm{0}}\\{\mathrm{3}{x}−\mathrm{2}{y}+{z}=\mathrm{3}}\end{cases} \\ $$$$\:\:\:\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{3}{z}^{\mathrm{2}} −\mathrm{4}{xy}+{yz}+{x}+\mathrm{2}{y}−\mathrm{3}{z}+\mathrm{7}=\mathrm{0} \\ $$
Answered by Her_Majesty last updated on 09/Aug/20
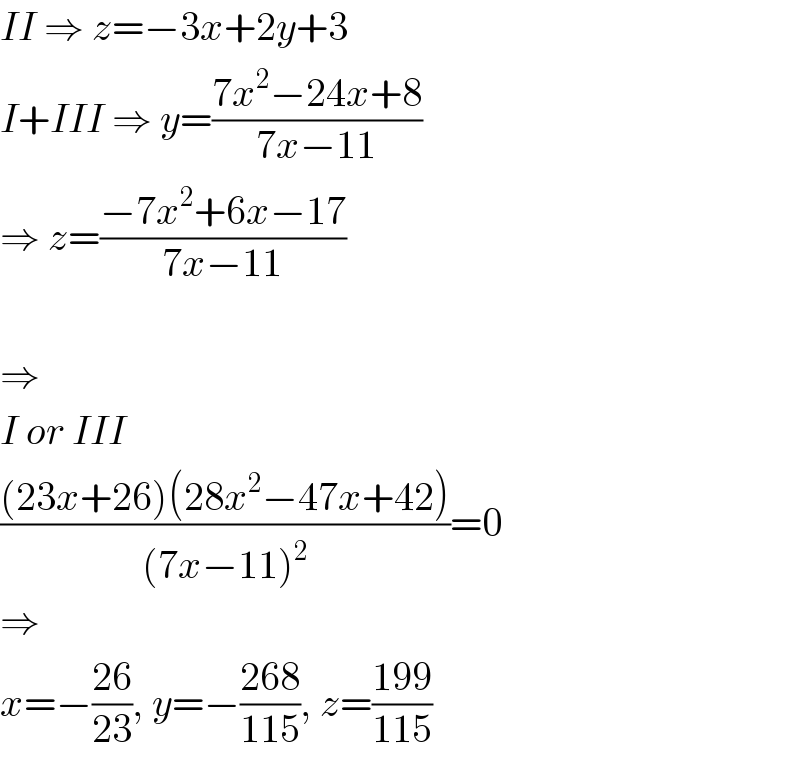
$${II}\:\Rightarrow\:{z}=−\mathrm{3}{x}+\mathrm{2}{y}+\mathrm{3} \\ $$$${I}+{III}\:\Rightarrow\:{y}=\frac{\mathrm{7}{x}^{\mathrm{2}} −\mathrm{24}{x}+\mathrm{8}}{\mathrm{7}{x}−\mathrm{11}} \\ $$$$\Rightarrow\:{z}=\frac{−\mathrm{7}{x}^{\mathrm{2}} +\mathrm{6}{x}−\mathrm{17}}{\mathrm{7}{x}−\mathrm{11}} \\ $$$$ \\ $$$$\Rightarrow \\ $$$${I}\:{or}\:{III} \\ $$$$\frac{\left(\mathrm{23}{x}+\mathrm{26}\right)\left(\mathrm{28}{x}^{\mathrm{2}} −\mathrm{47}{x}+\mathrm{42}\right)}{\left(\mathrm{7}{x}−\mathrm{11}\right)^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow \\ $$$${x}=−\frac{\mathrm{26}}{\mathrm{23}},\:{y}=−\frac{\mathrm{268}}{\mathrm{115}},\:{z}=\frac{\mathrm{199}}{\mathrm{115}} \\ $$
