Question Number 150171 by puissant last updated on 10/Aug/21
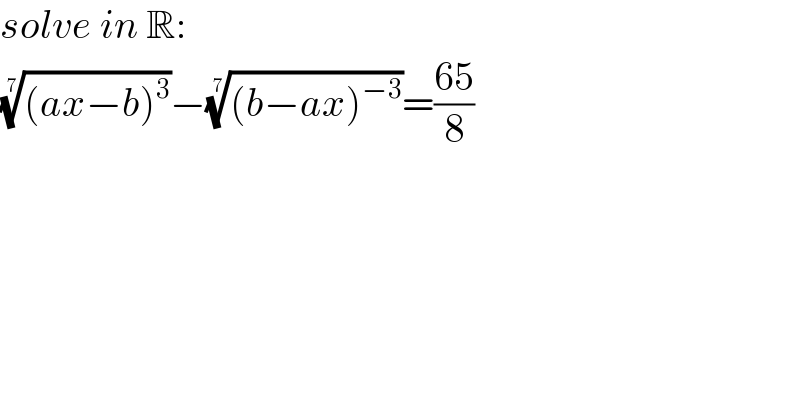
$${solve}\:{in}\:\mathbb{R}: \\ $$$$\sqrt[{\mathrm{7}}]{\left({ax}−{b}\right)^{\mathrm{3}} }−\sqrt[{\mathrm{7}}]{\left({b}−{ax}\right)^{−\mathrm{3}} }=\frac{\mathrm{65}}{\mathrm{8}} \\ $$
Answered by liberty last updated on 10/Aug/21
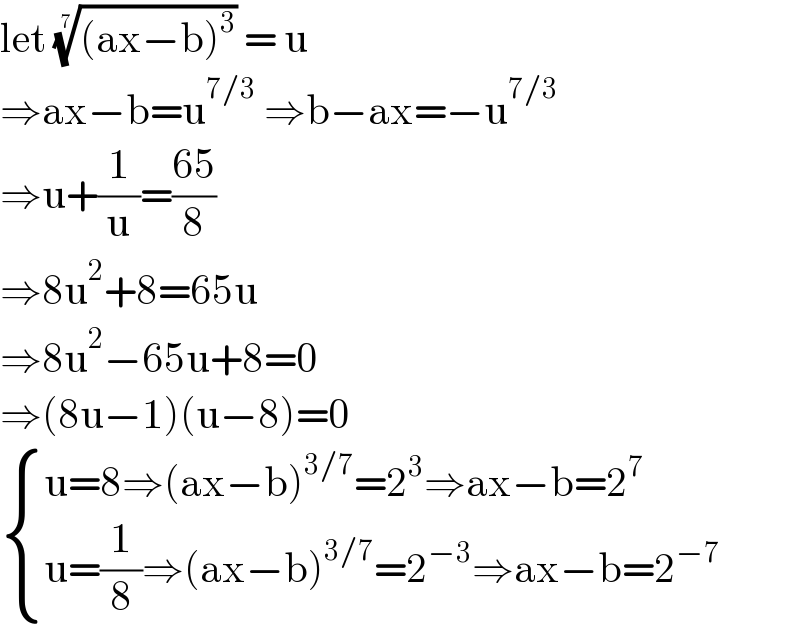
$$\mathrm{let}\:\sqrt[{\mathrm{7}}]{\left(\mathrm{ax}−\mathrm{b}\right)^{\mathrm{3}} }\:=\:\mathrm{u} \\ $$$$\Rightarrow\mathrm{ax}−\mathrm{b}=\mathrm{u}^{\mathrm{7}/\mathrm{3}} \:\Rightarrow\mathrm{b}−\mathrm{ax}=−\mathrm{u}^{\mathrm{7}/\mathrm{3}} \\ $$$$\Rightarrow\mathrm{u}+\frac{\mathrm{1}}{\mathrm{u}}=\frac{\mathrm{65}}{\mathrm{8}} \\ $$$$\Rightarrow\mathrm{8u}^{\mathrm{2}} +\mathrm{8}=\mathrm{65u} \\ $$$$\Rightarrow\mathrm{8u}^{\mathrm{2}} −\mathrm{65u}+\mathrm{8}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{8u}−\mathrm{1}\right)\left(\mathrm{u}−\mathrm{8}\right)=\mathrm{0} \\ $$$$\begin{cases}{\mathrm{u}=\mathrm{8}\Rightarrow\left(\mathrm{ax}−\mathrm{b}\right)^{\mathrm{3}/\mathrm{7}} =\mathrm{2}^{\mathrm{3}} \Rightarrow\mathrm{ax}−\mathrm{b}=\mathrm{2}^{\mathrm{7}} }\\{\mathrm{u}=\frac{\mathrm{1}}{\mathrm{8}}\Rightarrow\left(\mathrm{ax}−\mathrm{b}\right)^{\mathrm{3}/\mathrm{7}} =\mathrm{2}^{−\mathrm{3}} \Rightarrow\mathrm{ax}−\mathrm{b}=\mathrm{2}^{−\mathrm{7}} }\end{cases} \\ $$
Commented by puissant last updated on 10/Aug/21

$${thanks}\:{sir} \\ $$
