Question Number 166892 by mnjuly1970 last updated on 01/Mar/22
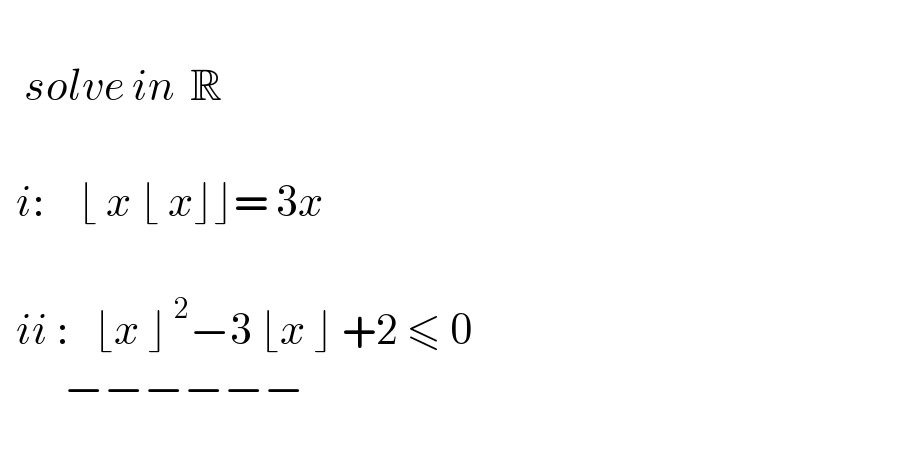
$$ \\ $$$$\:\:\:{solve}\:{in}\:\:\mathbb{R} \\ $$$$ \\ $$$$\:\:{i}:\:\:\:\:\lfloor\:{x}\:\lfloor\:{x}\rfloor\rfloor=\:\mathrm{3}{x} \\ $$$$ \\ $$$$\:\:{ii}\::\:\:\:\lfloor{x}\:\rfloor^{\:\mathrm{2}} −\mathrm{3}\:\lfloor{x}\:\rfloor\:+\mathrm{2}\:\leqslant\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:−−−−−− \\ $$$$ \\ $$
Answered by mathsmine last updated on 01/Mar/22
![[x[x]]=3x [x]=n x=n+f,f∈[0,1[ ⇒[(n+f)n]=3n+3f ⇒n^2 +[nf]=3n+3f n^2 −3n=3f−[nf]≤3+n ⇒n^2 −4n−3≤0⇒(n−2)^2 −7≤0 ⇒n∈[2−(√7),2+(√7)]n∈[0,4] n=0⇒f=0⇒x=0 n=1⇒1+[f]=3f+3⇒2=[f]−3f impossibl n=2⇒4+[2f]=6+3f⇒2=[2f]−3f impossible n=3⇒0=3f−[3f]⇒[3f]=3f∈{0,1,2} f=0,f=(1/3),f=(2/3),x=3,x=3+(1/3),x=3+(2/3) n=4⇒16+[4f]=12+3f ⇒4=3f−[4f]?impossible x∈{0,3,((10)/3),((11)/3)}](https://www.tinkutara.com/question/Q166905.png)
$$\left[{x}\left[{x}\right]\right]=\mathrm{3}{x} \\ $$$$\left[{x}\right]={n} \\ $$$${x}={n}+{f},{f}\in\left[\mathrm{0},\mathrm{1}\left[\right.\right. \\ $$$$\Rightarrow\left[\left({n}+{f}\right){n}\right]=\mathrm{3}{n}+\mathrm{3}{f} \\ $$$$\Rightarrow{n}^{\mathrm{2}} +\left[{nf}\right]=\mathrm{3}{n}+\mathrm{3}{f} \\ $$$$ \\ $$$${n}^{\mathrm{2}} −\mathrm{3}{n}=\mathrm{3}{f}−\left[{nf}\right]\leqslant\mathrm{3}+{n} \\ $$$$\Rightarrow{n}^{\mathrm{2}} −\mathrm{4}{n}−\mathrm{3}\leqslant\mathrm{0}\Rightarrow\left({n}−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{7}\leqslant\mathrm{0} \\ $$$$\Rightarrow{n}\in\left[\mathrm{2}−\sqrt{\mathrm{7}},\mathrm{2}+\sqrt{\mathrm{7}}\right]{n}\in\left[\mathrm{0},\mathrm{4}\right] \\ $$$${n}=\mathrm{0}\Rightarrow{f}=\mathrm{0}\Rightarrow{x}=\mathrm{0} \\ $$$${n}=\mathrm{1}\Rightarrow\mathrm{1}+\left[{f}\right]=\mathrm{3}{f}+\mathrm{3}\Rightarrow\mathrm{2}=\left[{f}\right]−\mathrm{3}{f}\:{impossibl} \\ $$$${n}=\mathrm{2}\Rightarrow\mathrm{4}+\left[\mathrm{2}{f}\right]=\mathrm{6}+\mathrm{3}{f}\Rightarrow\mathrm{2}=\left[\mathrm{2}{f}\right]−\mathrm{3}{f}\:{impossible} \\ $$$${n}=\mathrm{3}\Rightarrow\mathrm{0}=\mathrm{3}{f}−\left[\mathrm{3}{f}\right]\Rightarrow\left[\mathrm{3}{f}\right]=\mathrm{3}{f}\in\left\{\mathrm{0},\mathrm{1},\mathrm{2}\right\} \\ $$$${f}=\mathrm{0},{f}=\frac{\mathrm{1}}{\mathrm{3}},{f}=\frac{\mathrm{2}}{\mathrm{3}},{x}=\mathrm{3},{x}=\mathrm{3}+\frac{\mathrm{1}}{\mathrm{3}},{x}=\mathrm{3}+\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${n}=\mathrm{4}\Rightarrow\mathrm{16}+\left[\mathrm{4}{f}\right]=\mathrm{12}+\mathrm{3}{f} \\ $$$$\Rightarrow\mathrm{4}=\mathrm{3}{f}−\left[\mathrm{4}{f}\right]?{impossible} \\ $$$${x}\in\left\{\mathrm{0},\mathrm{3},\frac{\mathrm{10}}{\mathrm{3}},\frac{\mathrm{11}}{\mathrm{3}}\right\} \\ $$$$ \\ $$$$ \\ $$
Answered by mathsmine last updated on 01/Mar/22
![ii T^2 −3T+2≤0 (T−1)(T−2)≤0,T∈[1,2] [x]∈[1,2]⇒x∈[1,3[](https://www.tinkutara.com/question/Q166906.png)
$${ii} \\ $$$${T}^{\mathrm{2}} −\mathrm{3}{T}+\mathrm{2}\leqslant\mathrm{0} \\ $$$$\left({T}−\mathrm{1}\right)\left({T}−\mathrm{2}\right)\leqslant\mathrm{0},{T}\in\left[\mathrm{1},\mathrm{2}\right] \\ $$$$\left[{x}\right]\in\left[\mathrm{1},\mathrm{2}\right]\Rightarrow{x}\in\left[\mathrm{1},\mathrm{3}\left[\right.\right. \\ $$
