Question Number 83473 by M±th+et£s last updated on 02/Mar/20

$${solve}\:{in}\:{R} \\ $$$${sin}\left(\pi{ln}\left({x}\right)\right)+{cos}\left(\pi{ln}\left({x}\right)\right)=\mathrm{1} \\ $$
Answered by mind is power last updated on 02/Mar/20
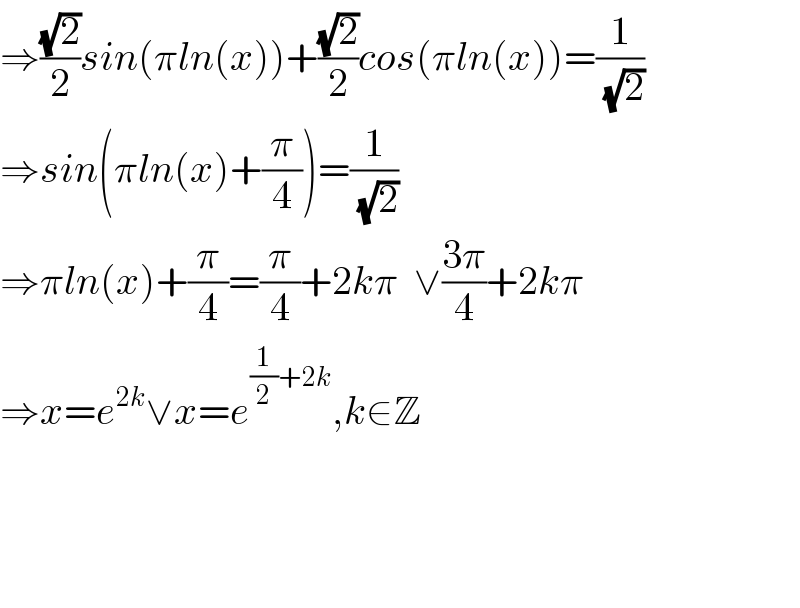
$$\Rightarrow\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}{sin}\left(\pi{ln}\left({x}\right)\right)+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}{cos}\left(\pi{ln}\left({x}\right)\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow{sin}\left(\pi{ln}\left({x}\right)+\frac{\pi}{\mathrm{4}}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\pi{ln}\left({x}\right)+\frac{\pi}{\mathrm{4}}=\frac{\pi}{\mathrm{4}}+\mathrm{2}{k}\pi\:\:\vee\frac{\mathrm{3}\pi}{\mathrm{4}}+\mathrm{2}{k}\pi \\ $$$$\Rightarrow{x}={e}^{\mathrm{2}{k}} \vee{x}={e}^{\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{2}{k}} ,{k}\in\mathbb{Z} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by M±th+et£s last updated on 02/Mar/20

$${thank}\:{you}\:{sir} \\ $$
