Solve-in-R-the-system-x-y-z-1-x-1-y-1-z-

Question Number 177763 by lapache last updated on 08/Oct/22

S o l v e i n R t h e s y s t e m

{\begin{cases} x + y = z \\ \frac{1}{x} + \frac{1}{y} = \frac{1}{z} \end{cases}

Commented by mr W last updated on 08/Oct/22

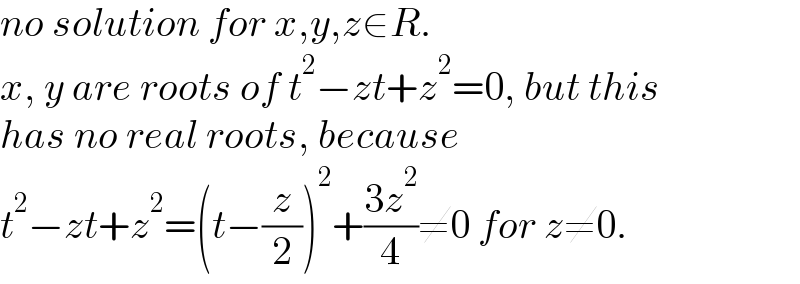
n o s o l u t i o n f o r x, y, z \in R .

x, y a r e r o o t s o f t^{2} - z t + z^{2} = 0, b u t t h i s

h a s n o r e a l r o o t s, b e c a u s e

t^{2} - z t + z^{2} = {(t - \frac{z}{2})}^{2} + \frac{3 z^{2}}{4} \neq 0 f o r z \neq 0 .

Facebook Tweet Pin