Question Number 153698 by mathocean1 last updated on 09/Sep/21

$${solve}\:{in}\:\mathbb{R} \\ $$$$\begin{cases}{{x}^{\mathrm{3}} −{y}^{\mathrm{3}} =\mathrm{19}}\\{{xy}=\mathrm{6}}\end{cases} \\ $$
Answered by amin96 last updated on 09/Sep/21
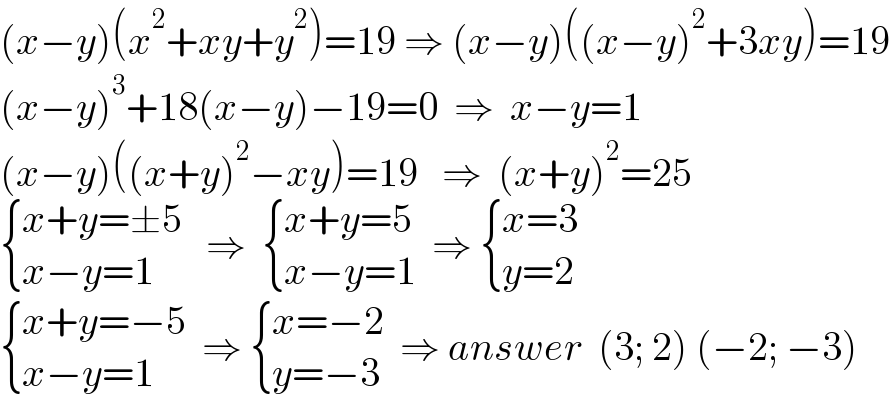
$$\left({x}−{y}\right)\left({x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} \right)=\mathrm{19}\:\Rightarrow\:\left({x}−{y}\right)\left(\left({x}−{y}\right)^{\mathrm{2}} +\mathrm{3}{xy}\right)=\mathrm{19} \\ $$$$\left({x}−{y}\right)^{\mathrm{3}} +\mathrm{18}\left({x}−{y}\right)−\mathrm{19}=\mathrm{0}\:\:\Rightarrow\:\:{x}−{y}=\mathrm{1} \\ $$$$\left({x}−{y}\right)\left(\left({x}+{y}\right)^{\mathrm{2}} −{xy}\right)=\mathrm{19}\:\:\:\Rightarrow\:\:\left({x}+{y}\right)^{\mathrm{2}} =\mathrm{25} \\ $$$$\begin{cases}{{x}+{y}=\pm\mathrm{5}}\\{{x}−{y}=\mathrm{1}\:}\end{cases}\:\:\:\Rightarrow\:\:\begin{cases}{{x}+{y}=\mathrm{5}}\\{{x}−{y}=\mathrm{1}}\end{cases}\:\:\Rightarrow\:\begin{cases}{{x}=\mathrm{3}}\\{{y}=\mathrm{2}}\end{cases} \\ $$$$\begin{cases}{{x}+{y}=−\mathrm{5}}\\{{x}−{y}=\mathrm{1}}\end{cases}\:\:\Rightarrow\:\begin{cases}{{x}=−\mathrm{2}}\\{{y}=−\mathrm{3}}\end{cases}\:\:\Rightarrow\:{answer}\:\:\left(\mathrm{3};\:\mathrm{2}\right)\:\left(−\mathrm{2};\:−\mathrm{3}\right) \\ $$
Answered by mr W last updated on 09/Sep/21
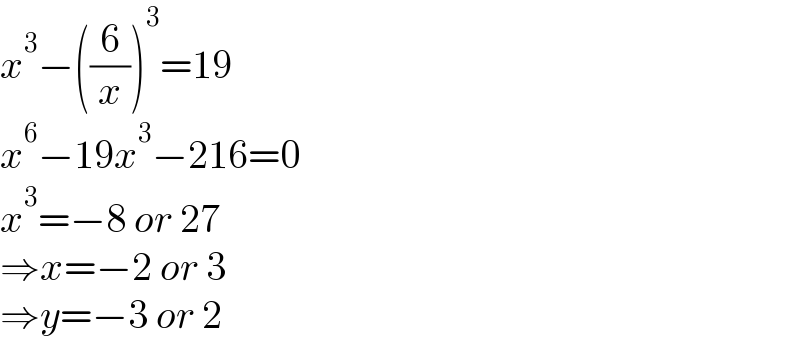
$${x}^{\mathrm{3}} −\left(\frac{\mathrm{6}}{{x}}\right)^{\mathrm{3}} =\mathrm{19} \\ $$$${x}^{\mathrm{6}} −\mathrm{19}{x}^{\mathrm{3}} −\mathrm{216}=\mathrm{0} \\ $$$${x}^{\mathrm{3}} =−\mathrm{8}\:{or}\:\mathrm{27} \\ $$$$\Rightarrow{x}=−\mathrm{2}\:{or}\:\mathrm{3} \\ $$$$\Rightarrow{y}=−\mathrm{3}\:{or}\:\mathrm{2} \\ $$
Commented by mathocean1 last updated on 09/Sep/21

$${thanks}\:{sirs} \\ $$
