Menu Close

Solve-in-real-numbers-the-equation-x-1-3-x-1-1-3-x-1-1-3-0-

Tinku Tara 0 Comments
Pin




Question Number 119848 by benjo_mathlover last updated on 27/Oct/20
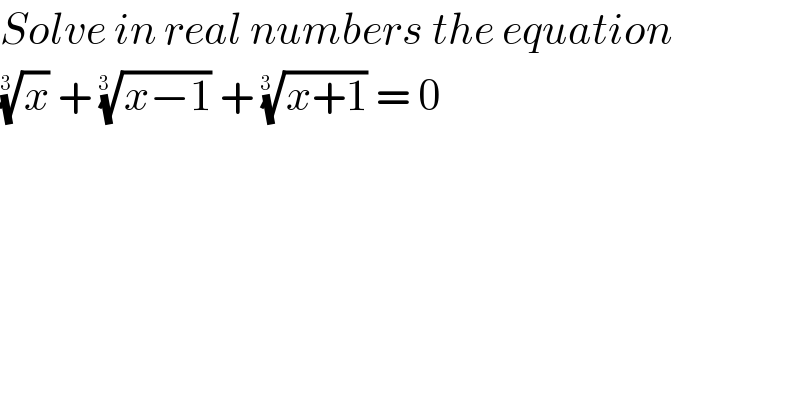
Solve in real numbers the equation (x)^(1/(3 )) + ((x−1))^(1/(3 )) + ((x+1))^(1/(3 )) = 0
Solveinrealnumberstheequationx3+x−13+x+13=0
Answered by 1549442205PVT last updated on 27/Oct/20
Applying the identity a^3 +b^3 +c^3 =3abc when a+b+c=0.Then (x)^(1/(3 )) + ((x−1))^(1/(3 )) + ((x+1))^(1/(3 )) = 0 gives us 3x=3^3 (√(x(x^2 −1))) ⇔x^3 =x(x^2 −1) ⇔x=0.Thus x=0 is unique root of given equation
Applyingtheidentitya3+b3+c3=3abcwhena+b+c=0.Thenx3+x−13+x+13=0givesus3x=33x(x2−1)⇔x3=x(x2−1)⇔x=0.Thusx=0isuniquerootofgivenequation

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *