Question Number 124763 by Mammadli last updated on 05/Dec/20

$$\boldsymbol{{Solve}}\:\boldsymbol{{in}}\:\boldsymbol{{the}}\:\boldsymbol{{order}}\:\boldsymbol{{of}}\:\boldsymbol{{finding}}\:\boldsymbol{{the}}\:\boldsymbol{{integrsting}}\:\boldsymbol{{stroke}}: \\ $$$$\mathrm{1}.\:\boldsymbol{{ydx}}−\left(\boldsymbol{{x}}^{\mathrm{3}} \boldsymbol{{y}}+\boldsymbol{{x}}\right)−\boldsymbol{{xdy}}=\mathrm{0} \\ $$$$\mathrm{2}.\:\left(\boldsymbol{{xy}}^{\mathrm{2}} +\boldsymbol{{y}}\right)\boldsymbol{{dx}}−\boldsymbol{{xdy}}=\mathrm{0} \\ $$
Commented by Mammadli last updated on 05/Dec/20
Sorry dear ser..
1. ydx-(x³y+x)dy=0
Answered by benjo_mathlover last updated on 05/Dec/20
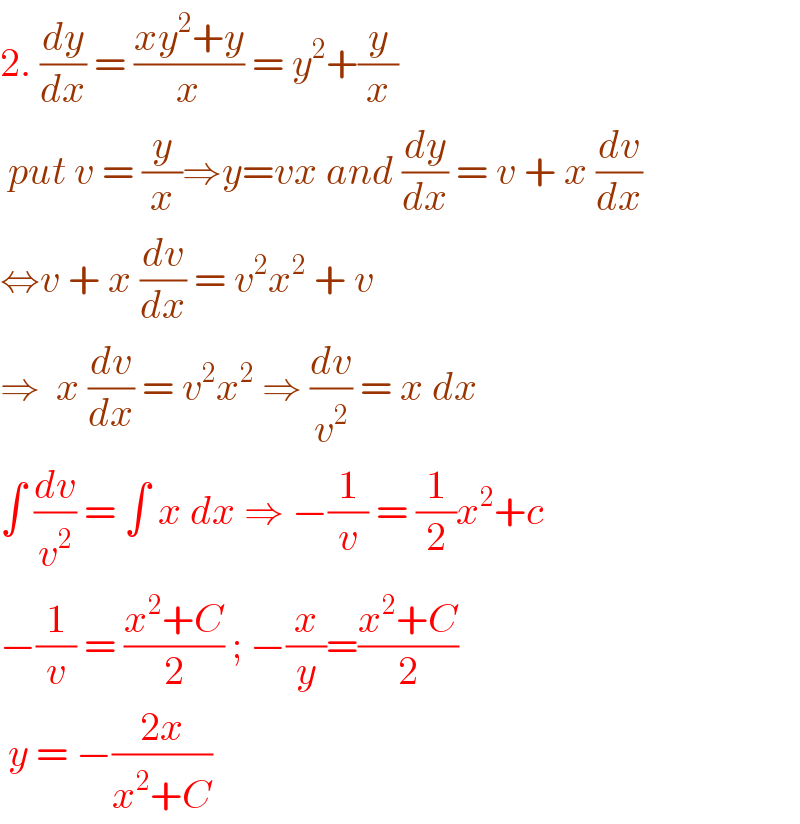
$$\mathrm{2}.\:\frac{{dy}}{{dx}}\:=\:\frac{{xy}^{\mathrm{2}} +{y}}{{x}}\:=\:{y}^{\mathrm{2}} +\frac{{y}}{{x}} \\ $$$$\:{put}\:{v}\:=\:\frac{{y}}{{x}}\Rightarrow{y}={vx}\:{and}\:\frac{{dy}}{{dx}}\:=\:{v}\:+\:{x}\:\frac{{dv}}{{dx}} \\ $$$$\Leftrightarrow{v}\:+\:{x}\:\frac{{dv}}{{dx}}\:=\:{v}^{\mathrm{2}} {x}^{\mathrm{2}} \:+\:{v}\: \\ $$$$\Rightarrow\:\:{x}\:\frac{{dv}}{{dx}}\:=\:{v}^{\mathrm{2}} {x}^{\mathrm{2}} \:\Rightarrow\:\frac{{dv}}{{v}^{\mathrm{2}} }\:=\:{x}\:{dx}\: \\ $$$$\int\:\frac{{dv}}{{v}^{\mathrm{2}} }\:=\:\int\:{x}\:{dx}\:\Rightarrow\:−\frac{\mathrm{1}}{{v}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} +{c} \\ $$$$−\frac{\mathrm{1}}{{v}}\:=\:\frac{{x}^{\mathrm{2}} +{C}}{\mathrm{2}}\:;\:−\frac{{x}}{{y}}=\frac{{x}^{\mathrm{2}} +{C}}{\mathrm{2}} \\ $$$$\:{y}\:=\:−\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +{C}} \\ $$
Commented by Mammadli last updated on 05/Dec/20
thk you dear ser, please:
ydx-(x³y+x)dy=0
Answered by liberty last updated on 06/Dec/20
![(1) y dx −(x^3 y+x)dy=0 let x = yv ⇒dx = v dy + y dv ⇔y(v dy +y dv)−(y^3 v^3 +yv)dy=0 ⇔ y^2 dv−y^3 v^3 dy = 0 ⇔ dv = y v^3 dy ; (dv/v^3 ) = y dy ∫ (dv/v^3 ) = ∫ y dy ; −(1/(2v^2 )) = (1/2)y^2 +c (y^2 /x^2 ) = −y^2 +C ; [ −2c = C ] y^2 ((1/x^2 )+1) = C ; y^2 = ((Cx^2 )/(x^2 +1)) y = ± ((λx)/( (√(x^2 +1)))) ; [ λ = (√C) ]](https://www.tinkutara.com/question/Q124783.png)
$$\left(\mathrm{1}\right)\:{y}\:{dx}\:−\left({x}^{\mathrm{3}} {y}+{x}\right){dy}=\mathrm{0} \\ $$$$\:{let}\:{x}\:=\:{yv}\:\Rightarrow{dx}\:=\:{v}\:{dy}\:+\:{y}\:{dv} \\ $$$$\Leftrightarrow{y}\left({v}\:{dy}\:+{y}\:{dv}\right)−\left({y}^{\mathrm{3}} {v}^{\mathrm{3}} +{yv}\right){dy}=\mathrm{0} \\ $$$$\Leftrightarrow\:{y}^{\mathrm{2}} \:{dv}−{y}^{\mathrm{3}} {v}^{\mathrm{3}} {dy}\:=\:\mathrm{0}\: \\ $$$$\Leftrightarrow\:{dv}\:=\:{y}\:{v}^{\mathrm{3}} \:{dy}\:;\:\frac{{dv}}{{v}^{\mathrm{3}} }\:=\:{y}\:{dy}\: \\ $$$$\int\:\frac{{dv}}{{v}^{\mathrm{3}} }\:=\:\int\:{y}\:{dy}\:;\:−\frac{\mathrm{1}}{\mathrm{2}{v}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{2}}{y}^{\mathrm{2}} +{c}\: \\ $$$$\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\:=\:−{y}^{\mathrm{2}} +{C}\:;\:\left[\:−\mathrm{2}{c}\:=\:{C}\:\right] \\ $$$${y}^{\mathrm{2}} \left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{1}\right)\:=\:{C}\:;\:{y}^{\mathrm{2}} \:=\:\frac{{Cx}^{\mathrm{2}} }{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$${y}\:=\:\pm\:\frac{\lambda{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}\:;\:\left[\:\lambda\:=\:\sqrt{{C}}\:\right]\: \\ $$$$ \\ $$
