Question Number 42304 by maxmathsup by imad last updated on 22/Aug/18

$${solve}\:{in}\:{Z}^{\mathrm{3}} \:\:\:\:{x}+\mathrm{2}{y}\:+\mathrm{3}{z}\:=\mathrm{12}\:\:. \\ $$
Commented by maxmathsup by imad last updated on 24/Aug/18
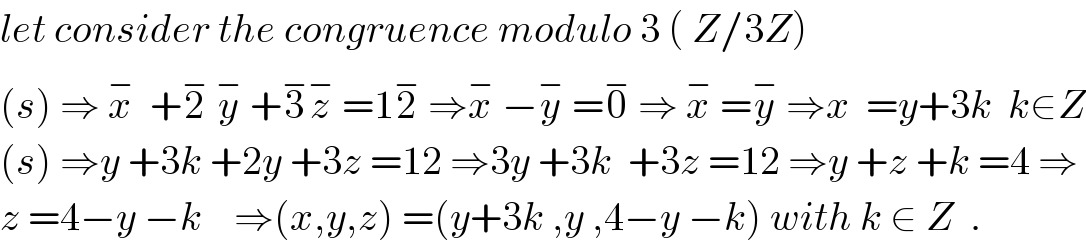
$${let}\:{consider}\:{the}\:{congruence}\:{modulo}\:\mathrm{3}\:\left(\:{Z}/\mathrm{3}{Z}\right)\: \\ $$$$\left({s}\right)\:\Rightarrow\:\overset{−} {{x}}\:\:+\overset{−} {\mathrm{2}}\:\overset{−} {{y}}\:+\overset{−} {\mathrm{3}}\overset{−} {{z}}\:=\mathrm{1}\overset{−} {\mathrm{2}}\:\Rightarrow\overset{−} {{x}}\:−\overset{−} {{y}}\:=\overset{−} {\mathrm{0}}\:\Rightarrow\:\overset{−} {{x}}\:=\overset{−} {{y}}\:\Rightarrow{x}\:\:={y}+\mathrm{3}{k}\:\:{k}\in{Z} \\ $$$$\left({s}\right)\:\Rightarrow{y}\:+\mathrm{3}{k}\:+\mathrm{2}{y}\:+\mathrm{3}{z}\:=\mathrm{12}\:\Rightarrow\mathrm{3}{y}\:+\mathrm{3}{k}\:\:+\mathrm{3}{z}\:=\mathrm{12}\:\Rightarrow{y}\:+{z}\:+{k}\:=\mathrm{4}\:\Rightarrow \\ $$$${z}\:=\mathrm{4}−{y}\:−{k}\:\:\:\:\Rightarrow\left({x},{y},{z}\right)\:=\left({y}+\mathrm{3}{k}\:,{y}\:,\mathrm{4}−{y}\:−{k}\right)\:{with}\:{k}\:\in\:{Z}\:\:. \\ $$
